Практическая работа №15 «Расчёт сводных характеристик выборки методом сумм».

Однофакторная параболическая модель второй степени - параболическая регрессия применяется, если факторный признак увеличивается в арифметической прогрессии, а результативный значительно быстрее. В этом случае уравнение регрессии будет иметь вид:

;

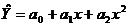В данном случае задача сводится к определению неизвестных параметров: а₀, а₁,. Величину параметров a₀, а₁ и а₂ находим как решение системы нормальных уравнений:

,

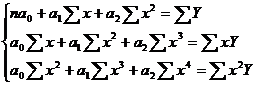Пример.По следующим данным, полагая, что зависимость между x и Y параболическая, определить значения коэффициентов a₀, а₁ и а₂:

х
Y

Решение.Для определения величин a₀, а₁ и а₂ необходимо вычислить следующие значения: åх, åY, åxY, åх², åх³, åx⁴, åх²Y. Расчёты рекомендуется проводить в Excel и оформлять в виде таблицы:

№ п/п	х	Y	xY	х2	х2Y	х3	x4		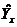D= Y -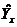
								2,098	-1,098
								3,488	-0,488
								4,903	1,097
								6,344	0,656
								7,809	0,191
								10,815	0,185
								15,51	0,49
								22,13	-1,13
								27,36	-0,36
								38,5	0,5
Итого

Система нормальных уравнений имеет вид:

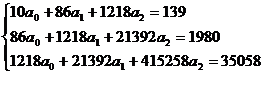
Решив данную систему методом Гаусса, получаем значения: a₀=0,734, а₁=1,352, а₂=0,0126. Следовательно, уравнение регрессии имеет вид: 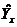=0,734+1,352х+0,0126х². Из таблицы видно, что вычисленные по уравнению регрессии значения 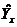незначительно отличаются от эмпирических данных.

Оценка обратной зависимости между Y и x, может быть дана на основе уравнения гиперболы: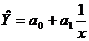

Величину параметров a₀ и а₁ находим как решение системы нормальных уравнений:

,

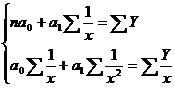Пример.По следующим данным, полагая, что зависимость между x и Y выражается уравнением гиперболы, определить значения коэффициентов a₀ и а₁:

х
Y

Решение.Для определения величин a₀ и а₁ расчёты рекомендуется проводить в Excel и оформлять в виде таблицы:

№ п/п	х	Y	1/х	Y/х	1/х2		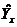Di
						9,73	4,27
			0,33	3,67	0,11	9,26	1,74
			0,25	2,75	0,062	9,20	1,80
			0,67	1,5	0,028	9,13	-0,13
			0,14	1,14	0,02	9,12	-1,12
			0,11	0,78	0,012	9,10	-2,1
			0,10	0,5	0,01	9,09	-4,09
Итого			2,6	24,34	1,242	64,63

Система нормальных уравнений имеет вид:

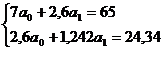
Решив данную систему методом Гаусса, получаем значения: a₀=9,02, а₁=0,71. Следовательно, уравнение регрессии имеет вид: 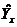=9,02+0,71/х.

Самостоятельная работа.

Выполняется в виде семестрового задания. Выдаётся после изучения первых двух разделов и в оформленном виде сдаётся в конце семестра. В задание включены 12 задач по изученным темам и основным формулам теории вероятности.

Система оценки работы:

№ задачи	Набираемый балл	Шкала перевода баллов в оценки
		менее 9	2 (неуд)
		9-12	3 (удовл.)
		13-16	4 (хорошо)
		17-20	5 (отлично)
всего