Практическая работа №14 «Расчёт сводных характеристик выборки методом произведений».

Признак – это основная отличительная черта, особенность изучаемого явления или процесса. Количественное представление признака называется показателем.

Результативный признак – исследуемый показатель процесса, характеризующий эффективность процесса.

Факторный признак – показатель, влияющий на значение результативного показателя.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака (Y) от факторных (x₁, x₂, …, x_n), выражаемой в виде уравнения регрессии:

Y = f(x₁, x₂, …, x_n).

Для характеристики связей между признаками используют следующие типы функций:

- линейную ;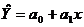

- гиперболическую ;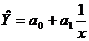

- показательную ;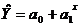

- параболическую ;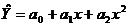

- степенную .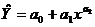

Линейная функция используется в случае, если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, гиперболическая – если связь между Y и x, наоборот, обратная. Параболическая или степенная функция применяются, если факторный признак увеличивается в арифметической прогрессии, а результативный значительно быстрее.

Линейная однофакторная регрессия: 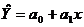. Для нахождения параметров a₀ и а₁ используют метод наименьших квадратов. Сущность метода заключается в нахождении параметров a₀ и а₁, при которых минимизируется сумма квадратов отклонений эмпирических значений результативного признака от теоретических, полученных по выбранному уравнению регрессии. Величину параметров a₀ и а₁ находим как решение системы нормальных уравнений:

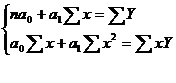, где n – объём исследуемой совокупности.

В уравнении регрессии свободный член регрессии коэффициент a₀ показывает совокупное влияние на результативный признак неучтённых (не выделенных для исследования) факторов; его вклад в значение результирующего показателя не зависит от изменения факторов; параметр а₁ – коэффициент регрессии – показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

Пример.По следующим данным, полагая, что зависимость между x и Y линейная, определить значения коэффициентов a₀ и а₁:

х
Y

Решение.Для определения величин a₀ и а₁ необходимо вычислить следующие значения: åх, åY, åxY, åх². Расчёты рекомендуется проводить в Excel и оформлять в виде таблицы:

№ п/п	х	Y	х2	xY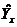
					2,07
					5,92
					9,77
					14,91
					20,05
					22,61
					29,03
Итого					104,36

Система нормальных уравнений имеет вид:

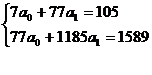
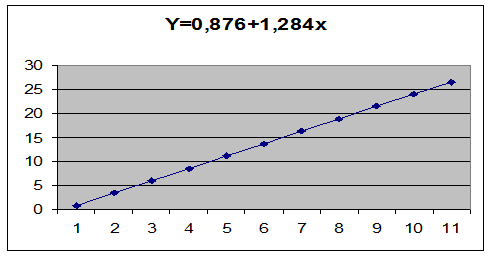
Решив данную систему методом Гаусса, получаем значения: a₀=0,876, а₁=1,284. Следовательно, 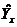=0,876+1,284х. Т.к. а₁>0, связь между признаками прямая (в случае обратной связи коэффициент регрессии отрицательный). При увеличении х на единицу, 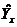- увеличивается на 1,284. Линейную модель удобно представлять графически: