Практическая работа №1: «Решение задач по алгебре событий».
Основные понятия и определения.
Пусть 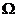 - пространство элементарных событий рассматриваемого опыта. Для каждого возможного в этом опыте события А выделим совокупность всех элементарных событий, наступление которых необходимо влечёт наступление А. Эти элементарные события благоприятствуют появлению А. Множество этих элементарных событий обозначим тем же символом А, что и соответствующее событие.
- пространство элементарных событий рассматриваемого опыта. Для каждого возможного в этом опыте события А выделим совокупность всех элементарных событий, наступление которых необходимо влечёт наступление А. Эти элементарные события благоприятствуют появлению А. Множество этих элементарных событий обозначим тем же символом А, что и соответствующее событие.
Таким образом, событие А состоит в том, что произошло одно из элементарных событий, входящих в указанное множество А. Мы отождествляем событие А и соответствующее ему множество А элементарных событий.
Событие называется достоверным, если оно наступает в результате появления любого элементарного события. Обозначение: 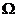 .
.
Невозможным назовём событие, не наступающее ни при каком элементарном событии. Обозначение: Æ.
Пример.В опыте с кубиком достоверным является событие, что выпадет число, меньшее 7. Невозможным – выпадет отрицательное число.
Суммой (или объединением) двух событий А и В назовём событие А+В (или АÈВ), происходящее тогда и только тогда, когда происходит или А, или В. Сумме событий А и В соответствует объединение множеств А и В. Очевидные соотношения: А+Æ=А, А+ 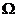 =
= 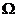 , А+А=А.
, А+А=А.
Пример.Событие «выпало чётное» является суммой событий: выпало 2, выпало 4, выпало 6.
Произведением (или пересечением) двух событий А и В назовём событие АВ (или АÇВ), которое происходит тогда и только тогда, когда происходит и А, и В. Произведению событий А и В соответствует пересечение множеств А и В.
Очевидные соотношения: АÆ=Æ, А 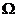 =А, АА=А.
=А, АА=А.
Пример.«Выпало 5» является пересечением событий: выпало нечётное и выпало больше 3-х.
Два события назовём несовместными, если их одновременное появление в опыте невозможно, т.е. АВ=Æ.
Пример.Выпало чётное число и выпало нечётное число – события несовместные.
Событие 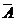 назовём противоположным к А, если оно происходит тогда и только тогда, когда А не происходит. Очевидные соотношения: А+
назовём противоположным к А, если оно происходит тогда и только тогда, когда А не происходит. Очевидные соотношения: А+ 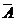 =
= 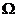 , А
, А 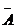 =Æ,
=Æ, 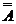 =А.
=А.
Пример.Выпало чётное число и выпало нечётное число – события противоположные.
Разностью событий А и В назовём событие А\В, происходящее тогда и только тогда, когда происходит А, но не происходит В. Очевидные соотношения: 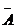 =
= 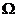 \А, А\В=А
\А, А\В=А 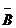 .
.
Операции сложения и умножения обладают следующими свойствами: А+В=В+А, АВ=ВА, А(В+С)=АВ+АС, А(ВС)=(АВ)С.
Пример.Производится два выстрела по цели. Пусть событие А – попадание в цель при первом выстреле и В – при втором, тогда 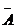 и
и 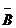 - промах соответственно при первом и втором выстрелах. Обозначим поражение цели событием С и примем, что для этого достаточно хотя бы одного попадания. Требуется выразить С через А и В.
- промах соответственно при первом и втором выстрелах. Обозначим поражение цели событием С и примем, что для этого достаточно хотя бы одного попадания. Требуется выразить С через А и В.
Решение.Цель будет поражена в следующих случаях: попадание при первом и промах при втором; промах при первом и попадание при втором; попадание при первом и втором выстрелах. Перечисленные варианты можно соответственно записать: А 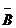 ,
, 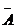 В и АВ. Интересующее нас событие заключается в наступлении или первого, или второго, или третьего вариантов (хотя бы одного), то есть
В и АВ. Интересующее нас событие заключается в наступлении или первого, или второго, или третьего вариантов (хотя бы одного), то есть
С= А 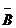 +
+ 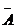 В+АВ.
В+АВ.
С другой стороны, событие 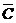 , противоположное С, есть промах при двух выстрелах, то есть
, противоположное С, есть промах при двух выстрелах, то есть 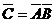 , отсюда искомое событие С можно записать в виде С=
, отсюда искомое событие С можно записать в виде С= 
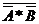 .
.
