Напишите уравнение высоты BK в треугольнике ABC, если он задан своими вершинами: А(4;2); В(5;8); С(5;5).

9. Напишите уравнение прямой линии, проходящей через точки 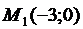и .

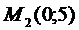10. Вычислить угол между прямым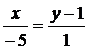и: и .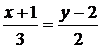

Дан треугольник с вершинами в точках А ( 1; 1), В(– 4; 3) и С(2; 2). Составьте уравнение медианы АK.

12. Определить угол между прямыми линиями: х + 3у – 2 = 0 и 2у = х + 5.

Даны три вершины треугольника: А(–2;–2), В(7;–6) и С(1;2). Составить уравнение прямой АМ, параллельной стороне ВС.

Геометрические тела и поверхности. Объёмы и площади поверхностей геометрических тел.

В основании прямого параллелепипеда лежит ромб, диагонали которого равны 12 см и 16 см, а высота параллелепипеда равна 8 см. Определить площадь его полной поверхности.

2. В прямом параллелепипеде стороны оснований равны 7 см и 4 см, угол между ними 60 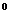. Определить объём параллелепипеда, если боковая поверхность равна 220 см 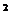. 3.Стороны основания прямого параллелепипеда равны 6 см и 8 см и образуют угол в 30^о. Боковое ребро равно 5 см. Найдите полную поверхность этого параллелепипеда.

В основании прямого параллелепипеда лежит ромб, диагонали которого равны 12 см и 16 см, а высота параллелепипеда равна 8 см. Найти объём параллелепипеда.

В прямоугольном параллелепипеде стороны основания равны 9 дм 12 дм, а высота параллелепипеда 7 дм. Найти объём параллелепипеда.

6. Рёбра прямоугольного параллелепипеда относятся как 3:7:8, площадь поверхности равна 808 м 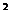.Определить длины ребер параллелепипеда.

Диагональ правильной четырехугольной призмы равна 3,5 м, а диагональ боковой грани 2,5 м. Найти объём призмы.

В прямоугольном параллелепипеде стороны основания равны 7 дм и 24 дм, а высота параллелепипеда равна 8 дм. Определить площадь полной поверхности параллелепипеда.

9. Основание прямой призмы – прямоугольный треугольник с катетом 6 дм и острым углом 45⁰. Объем призмы равен 108 дм 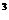. Найти площадь полной поверхности призмы.

10. В прямоугольном параллелепипеде стороны основания равны 7 дм и 24 дм, а высота параллелепипеда равна 8 дм. Определить площадь диагонального сечения. 11. Основания усеченной пирамиды равны 27см² и 12 см², высота равна 5 см. Вычислить высоту соответствующей полной пирамиды.

12. В пирамиде сечение параллельное основанию делит высоту на две равные части. Площадь основания равна 200 см². Определить площадь сечения .

Высота пирамиды разделена на три равные части и через точки деления проведены плоскости, параллельные основанию. Площадь основания равна

270 см 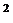. Определить площади полученных сечений.

14. Боковое ребро правильной четырехугольной пирамиды наклонено к плоскости основания под углом 45 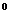. Диагональ основания пирамиды равна 8 см. Найти высоту пирамиды.

15. Боковое ребро правильной четырехугольной пирамиды наклонено к плоскости основания под углом 60 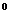и равно 10 см. Найти площадь основания пирамиды.

16. Основание пирамиды – прямоугольный треугольник, один из катетов которого равен 12 дм, противолежащий ему острый угол равен 60 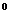. Каждое боковое ребро равно 13 дм. Найти объём пирамиды.