X. движение границы раздела двух жидкостей в пористой среде

Вытеснение нефти водой

При проектировании разработки нефтяных месторождений в условиях водонапорного режима, когда нефть вытесняется в скважины напором краевых вод, необходимо учесть стягива­ние контура нефтеносности.

С вытеснением нефти водой приходится встречаться и при расчетах деформации водонефтяного контакта. Аналогичные задачи возникают и при эксплуатации газовых месторождении с краевой или подошвенной водой.

Предполагается, что вытеснение «поршневое» и граница раз­дела двух жидкостей является некоторой поверхностью. При решении задач о вытеснении учитывается различие в вязкостях нефти и воды. Плотности нефти и воды считаются одинако­выми. Это дает возможность рассматривать границу раздела двух жидкостей вертикальной. В общем случае на границе раз­дела двух жидкостей с различными физическими свойствами

происходит преломление ли­ний тока. Учет этого пре­ломления и составляет глав­ную трудность в точном реше­нии задачи о вытеснении неф­ти водой (или газа водой). Линии тока не преломляются при прямолинейно-поступа­тельном и радиальном движе­ниях, когда в начальный мо­мент времени они перпендику­лярны границе раздела. В этих случаях получены точные решения, в которых жидкости (нефть, вода) принимаются несжимаемыми, пласт — гори­зонтальным, режим пласта — водонапорным, фильтрация — происходящей по линейному закону.

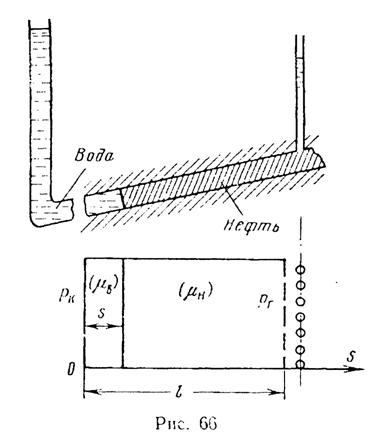
При прямолинейном движении границы раздела (рис. 66), когда в начальном положении она параллельна галерее, в пласте с постоянными мощностью, пористостью и проницае­мостью формула для дебита галереи имеет вид

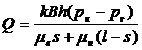(X.1)

где l - длина пласта; s — расстояние от контура питания до водонефтяного контакта.

Из приведенной формулы видно, что дебит нефти при задан­ных постоянных значениях р_н и р_гвозрастает при продвижении границы раздела, если m_н>m_в.

Время вытеснения нефти водой в случае прямолинейно-поступательного движения границы раздела подсчитывается по формуле

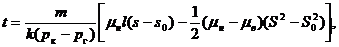(X.2)

где s₀ — координата, определяющая положение границы раз­дела в начальный момент времени.

Чтобы найти время полного вытеснения нефти, нужно в фор­муле (Х.2) положить s = l.

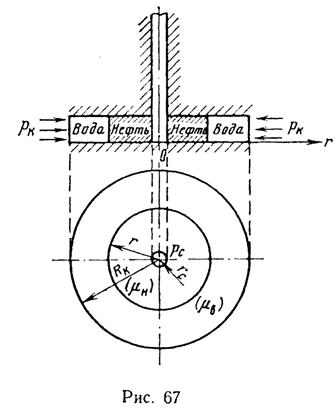
Аналогичная картина наблюдается и в условиях плоскорадиальной фильтрации (рис. 67). В этом случае дебит оп­ределяется по формуле

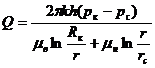(X.3)

где r — координата, определя­ющая положение границы раз­дела нефть — вода в момент t.

Время радиального перемещения границы от начального по­ложения r = r_o (при t = 0) до r находится по формуле

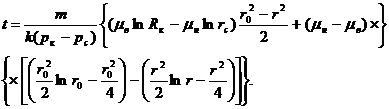(X.4)

Различие вязкости нефти и воды существенно влияет как на время извлечения нефти (газа) из пласта, так и на характер продвижения контура водоносности.

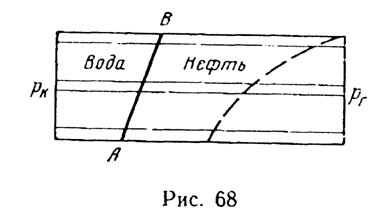
Допустим, что первоначальное положение водонефтяного контакта в пласте А В не параллельно галерее (рис. 68). Для решения задачи о продвижении водонефтяного контакта в ука­занных условиях используют приближенный метод «полосок», предложенный В. Н. Щелкачeвым. Рассматривается послойное движение частиц. Выделяют несколько узких полосок, и в пре­делах каждой полоски рассматривают вытеснение как поршне­вое с контуром водоносности, параллельным галерее. При усло­вии m_н > m_в скорость точки В больше, чем скорость точки А, отсюда можно сделать вывод, что скорость движения «водяного языка» в наиболее вытянутой точке по мере его движения к галерее (или прямолинейной цепочке скважин) растет быст­рее, чем скорость его основания и остальной части контура водо­носности.

§ 2. Конус подошвенной воды. Определение предельного безводного дебита скважины

При отборе нефти (газа) из гидродинамически несовершен­ной по степени вскрытия скважины в пласте с подошвенной во­дой происходит деформация границы водонефтяного контакта. Образующееся повышение уровня воды называется конусом подошвенной воды (рис. 69). При увеличении дебита конус под­нимается, и при некотором предельном значении Q = Q_пред про­исходит прорыв подошвенной воды в скважину. Условием ста­бильности конуса является равенство градиента давления на вершине конуса удельному весу воды:

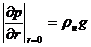(X.5)

Методы расчета предельных безводных дебитов были пред­ложены И. А. Чарным, II. Ф. Ивановым, Н. С. Пискуновым, Д. А. Эфросом, Г. Дж. Мейером, О. А. Гайдаром и др.

Н. А. Чариый, сопоставляя движение нефти при наличии

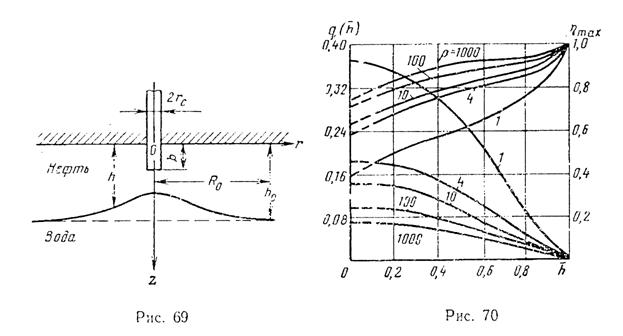
конуса подошвенной поды с напорным равнодебитным движе­нием нефти в пласте постоянной мощности h(R_о)=h_о и исполь­зуя условие стабильности конуса (Х.5), получил формулу для верхнего значения предельного безводного дебита в однородно-анизотропном пласте, в каждой точке которого значение коэф­фициента проницаемости в горизонтальном направлении k_гор резко отличается от значения коэффициента проницаемости в вертикальном направлении k_нерт, в виде:

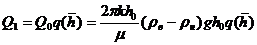(X.6)

где 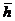= b/h_о; q( 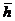) —безразмерный дебит.

Кривые q( 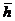) для различных значений r = R₀/xh₀ показаны на рис. 70. Здесь х = 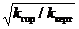- коэффициент, учитывающий анизотропию пласта.

На рис. 70 приведены также графики 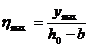для расчета высоты подъема конуса у_мах, соответствующей Q₁.

Рассматривая предельный случай, в котором вершина водя­ного конуса находится у забоя скважины, П. Ф. Иванов вывел приближенную формулу для предельного безводного дебита скважины, аналогичную формуле (VI.5) дебита скважины при безнапорном движении

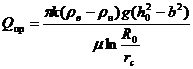(X.7)

Задача 95

В полосообразном пласте имеет место поршневое вытесне­ние нефти водой. Первоначальная граница раздела вертикальна и параллельна галерее. Длина пласта L_к = 5 км, длина зоны, занятой нефтью в начальный момент, — 1 км. Динамические коэффициенты вязкости нефти m_н = 4 сП, воды m_в = 1 сП. Найти отношение дебита галереи в начальный момент эксплуатации и дебита той же галереи, когда весь пласт заполнен нефтью. Определить отношение времени вытеснения нефти водой и нефти нефтью.

Ответ: Q_н-в/Q_н-н = 2,5; Т_н-в/Т_н-н =0,325

Задача 96

Определить время продвижения нефти от контура водонос­ности до скважины в случае плоскорадиального движения по закону Дарси и сопоставить его со временем прохождения того же пути водой. Определить дебит скважины в начальный мо­мент времени и в момент обводнения. Расстояние до контура питания R_к = 10 км, первоначальный радиус водонефтяного контакта r_о = 450 м, мощность пласта h = 10 м, пористость пласта m = 20%, коэффициент проницаемости пласта k = 0,2 Д, коэф­фициенты вязкости нефти m_н = 5 мПа×с, воды m_в = l мПа×с, давление на контуре питания р_к=9,8 МПа (100 кгс/см²), дав­ление на забое скважины р_с = б,86 МПа (70 кгс/см²), радиус скважины r_с = 0,1 м.

Ответ:Т = 46,2 лет; Т_в = 12,5 лет; Q_нач = 72,2 м³/сут; Q_кон = 283 м³/сут.

Задача 97

Положение водонефтяного контакта в пористом пласте, изображенном в плане на рис. 71, в начальный момент времени показано линией ab, не параллельной галерее. Найти скорость фильтрации в точках а и b.

Определить положение точки а, когда точка b достигнет галереи. Расстояние от галереи до контура питания L_к =10 км, расстояние от контура питания до точки а рав­но х_а = 9200 м, расстояние до точки b x_b = 9500 м, коэффи­циенты вязкости нефти m_н = 6 сП, воды m_в = 1 сП, коэффициент проницаемости пласта k = 1Д, коэффициент пористости пласта т = 20%, давление на контуре питания р_к = 9,8 МПа (100 кгс/см²), давление на забое галереи р_г= 6,86 МПа (70 кгс/см²).

Решение.Задачу будем решать приближенным методом по­лосок, предложенным В. Н. Щелкачевым. Выделим впласте две узкие полоски в окрестностях то­чек а и b и будем считать, что в каждой из них граница раздела нефть — вода вертикальна и па­раллельна галерее. В каждой по­лоске перемещение границы раз­дела будем рассчитывать по фор­мулам для поршневого прямоли­нейно-параллельного вытесне­ния.

Найдем скорости фильтрации в точках а и b.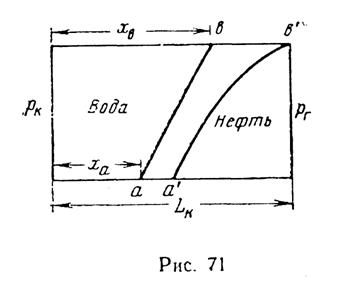

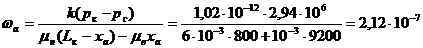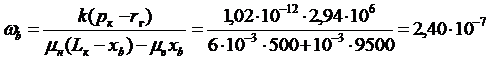м/с,

м/с.

Определим время, за которое точка b достигнет галереи:

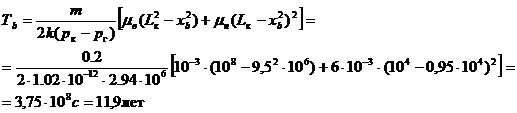
Найдем положение точки а, когда точка b достигнет галереи:

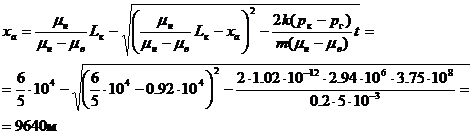
т. е. точка а будет отстоять от галереи на 360 м и граница раз­дела нефть—вода примет положение a'b'.

Задача 98

Определить предельный безводный дебит скважины, вскрыв­шей нефтяной пласт с подошвенной водой, если R_к = 200 м, радиус скважины r_с= 10 см, нефтенасыщенная мощность пласта h_o =12 м, разность плотностей воды и нефти r_в — r_н = 0,398 г/см³, динамический коэффициент вязкости нефти m_н = 2,54 сП. Пласт считать однородным по проницаемости (х = 1), k = 1 Д.

Задачу решить по формуле Н. Ф. Иванова и по методу, пред­ложенному И. А. Чарным при мощности вскрытой части пласта b, равной 6 м и 2 м.

Решение.Определим предельный безводный дебит по при­ближенной формуле Н. Ф.Иванова

1)

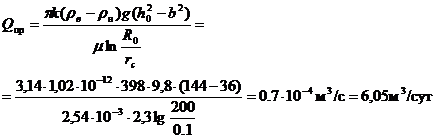
По графикам И. А. Чарного (см. рис. 70) найдем 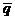(r, h) = Q_пр/Q₀, где

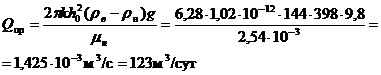
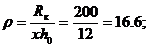
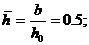
q(16.6; 05) = 0.097, откуда Q_пр = 0,097×123 = 11,95 м³/сут

2)

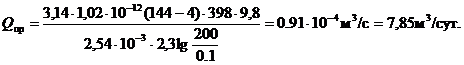
q(16.6; 0,166) – 0,14, Q_пр=0,14×123 = 17,2 м³/сут

Как видно из расчетов, формула II. Ф. Иванова дает резко заниженный предельный безводный дебит по сравнению с пре­дельным безводным дебитом по методу И. А. Чарного.

Задача 99

По данным предыдущей задачи определить высоту подъема конуса подошвенной воды по методу И. А. Чарного.

Решение.

1.Определим по графикам И. А. Чарного h_max = y_max/(h_o—b} в зависимости от р = R₀/xh₀ = 16,6 и

;

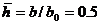h_max = 0,81, откуда высота подъема вершины конуса

У_max = 0,81(12-6)=4,86 м.

2)h_max(16,6; 0,167) = 0,7,

У_max = 0,7(12-2) = 7 м.

Задача 100

Определить предельно допустимую депрессию при отборе нефти из скважины, вскрывающей пласт с подошвенной водой на глубину b = 12,5 м. Мощность нефтеносной части пласта в от­далении от скважины h_о = 50 м, проницаемость пласта k = 0,5Д, плотность воды r_в = 1 г/см³, плотность нефти r_н = 0,7 г/см³, дина­мический коэффициент вязкости нефти m_н = 2 сП, расстояние до контура питания R_к = 200м, диаметр скважины d_c = 21,9 см, пласт считать изотропным (х = k_гор/k_верт = 1).

Решение.По методу И. А. Чарного определим приближенное значение предельного безводного дебита нефти

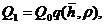
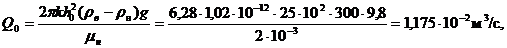
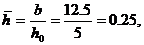
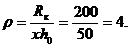
По графику зависимости q от р и 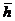(см. рис. 70) при значе­нии р = 4 и 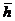= 0,25 получаем

q(0.25; 4) = 0,173

Q₁ = 1.175×10^-2×0.173 = 2.04×10^-3 м³/с.

Предельно допустимую депрессию найдем из решения Маскета о притоке к скважине гидродинамически несовершенной по степени вскрытия

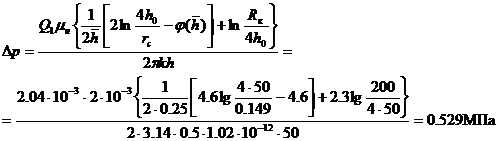
здесь значение функции 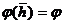(0,25) = 4,6 (см. рис. 34).