Отпечатано с готовых диапозитивов

В. А. Евдокимова

И. Н. Кочина

Сборник задач

По подземной

Гидравлике

Учебное пособие для вузов

Издание второе, стереотипное

Перепечатка с издания 1979 г.

Первое издание допущено Министерством высшего

и среднего специального образования СССР в

качестве учебного пособия для студентов высших

учебных заведений, обучающихся по специальности

«Технология и комплексная механизация разработки нефтяных и газовых месторождений»

АльянС

Москва 2007

УДК 622.276 (0.75.8)

ББК

Е15

Евдокимова В.А., Кочина И.Н.

Е15 Сборник задач по подземной гидравлике:

Учебное пособие для вузов. — 2-е изд., стереотипное. Перепечатка с издания 1979 г. - М.: ООО ИД «Альянс», 2007. - 168 с.

Приведенные в учебном пособии ладами, можно использовать при проектировании разработки нефтяных и газовых месторождений. Первое, издание выпущено в 1979 году издательством «Недра». Учебное пособие рассчитано на студентов нефтяных вузов и факультетов.

ISBN 978-5-903034-13-0

© ООО ИД «Альянс», 2007

ЕВДОКИМОВА Вера Алексеевна

КОЧИНА Ираида Николаевна

Сборник задач по подземной гидравлике

Учебное пособие для вузов

Издание второе, стереотипное

Перепечатка с издания 1979 г.

Подписано в печать 27.10.06. Формат 60x90/16.

Гарнитура Литературная. Печати офсетная Исч. л. 10,5.

Тираж 1000 экз. Заказ 61061

ООО Издательский дом «Альянс»

105120, Москва, ул. Сергия Радонежского, д.9, стр. 5

Тел./факс (499) 973-06-80, 973-09-41

973-17-82, 973-17-96, 973-18-56

[email protected]

Отпечатано с готовых диапозитивов

Г. Саратов, ул. Волжская, д.28

ЗАО "Типография "Полиграфист"

ПРЕДИСЛОВИЕ

В сборник включены задачи, которые можно использовать при проектировании нефтяных и газовых месторождений, ре­шении различных проблем гидротехники, инженерной геологии, гидрогеологии, ирригации и горного дела. Решение многих задач подземной гидравлики полезно также при расчете ис­кусственных фильтров различных конструкций, пористых катализаторов и т. д.

При составлении сборника задач авторы использовали мно­голетний опыт преподавания курса «Подземная гидравлика» в Московском институте нефтехимической и газовой промышлен­ности им. акад. И. М. Губкина. В сборник, в основном, вошли задачи, которые предлагались студентам на практических за­нятиях.

Настоящее пособие предназначено также для студентов специальностей «Геология и разведка нефтяных и газовых ме­сторождений» и «Экономика и организация нефтяной и газо­вой промышленности».

Сборник задач состоит из 15 глав. К каждой главе дает­ся краткая теория. Ко всем задачам имеются ответы. Типовые и наиболее сложные задачи приведены с решениями. В реше­ниях некоторых задач даются выводы формул, отсутствующие в учебной литературе.

В сборник входят задачи на определение фильтрационных характеристик пластов, расчет производительности нефтяных игазовых эксплуатационных и нагнетательных скважин в од­нородных и неоднородных по проницаемости пористых плас­тах, а также в деформируемых трещиноватых пластах, учет интерференции скважин (совершенных и несовершенных), рас­чет продвижения водонефтяного контакта, определение высо­ты подъема конуса подошвенной воды при эксплуатации неф­тяных или газовых месторождений с подошвенной водой, оп­ределение дебитов и распределения давления при движении га­зированной жидкости в пористой среде, изменение дебитов и давлений при нестационарном движении упругой жидкости и газа в деформируемой пористой среде, вытеснение нефти водой по теории Баклея — Леверетта и др.

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ФИЛЬТРАЦИИ

Фильтрация

Фильтрацией называется движение жидкостей, газов и их смесей в пористых и трещиноватых средах, т. е. в твер­дых телах, пронизанных системой сообщающихся между собой пор и микротрещин.

Фильтрация жидкостей и газов по сравнению с движением в трубах и каналах обладает некоторыми специфическими осо­бенностями.

Фильтрация происходит по чрезвычайно малым в попереч­ных размерах норовым каналам при очень малых скоростях движения жидкостей. Силы трения при движении жидкости в пористой среде очень велики, так как площади соприкоснове­ния жидкостилощади соприкоснове­ния жидкое с твердыми частицами огромны.

Пористая среда характеризуется коэффициентами пористо­сти и проснетпости.

Коэффициент пористости тесть отношение объема­ пор (τ_пор) ко всему объему пористой среды (τ)

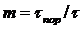(I.1)

Под пористостью в теории фильтрации понимается активная пористость, которая учитывает только те поры и микротрещины, которые соединены между собой и че­рез которые может фильтроваться жидкость.

Коэффициентом просветности п называется от­ношение площади просветов (ω_просв) в данном сечении пори­стой среды ко всей площади этого сечения (ω)

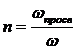(I.2)

Можно показать, что среднее по длине пласта значение просветности равно пористости, т. е.

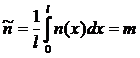(I.3)

поэтому среднее значение площади просветов

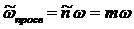
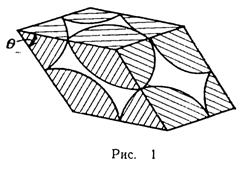
Упрощенной моделью пористой среды является модель фиктивного грунта. Фиктивный грунт состоит из шари­ков одного диаметра, уложенных определенным образом. Основным элементом (основной ячейкой) фиктивного грунта яв­ляется ромбоэдр, который получится, если принять центры восьми соприкасающихся частиц за вершины углов (рис. 1), В зависимости от острого угла θ боковой грани ромбоэдра ук­ладка шаров более или менее плотная.

Угол θ изменяется в пределах от 60° до 90°. Углу θ = 60° соответствует наиболее плотная укладка шаров, углу θ = 90° — наиболее свободная.

Пористость фиктивного грунта определяется по формуле Ч. Слихтера

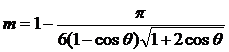(I.4)

из которой следует, что пористость зависит не от диаметра частиц, а лишь от их взаимного расположения, которое опре­деляется углом θ.

Чтобы формулы для фиктивного грунта можно было при­менять для естественного грунта, нужно заменить реальный грунт эквивалентным ему фик­тивным, который должен иметь такое же гидравличес­кое сопротивление, как у ес­тественного грунта.

Диаметр частиц такого фиктивного грунта называется эффек­тивным диаметром (d₃). Эффективный диаметр оп­ределяется в результате ме­ханического анализа грунта. Его просеивают через набросит с различной площадью отверстий и, таким образом, разде­ляют на фракции. За средний диаметр каждой фракции прини­мают среднее арифметическое крайних диаметров, т.е.

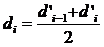
Затем строят кривую механического (фракционного) соста­ва грунта, откладывая по оси абсцисс средние диаметры фрак­ций d_i а но оси ординат — сумму масс фракций Δg₁+ Δg₂ + + ... + Δg_i в % от общей массы.

Последняя точка кривой имеет абсциссу, равную d_n, и ор­динату Δg₁+ Δg₂+... + Δg_n =100% (рис. 2).

Существует много способов определения эффективного диаметра. По способу А. Газена d_э определяется по кривой механического состава. За эффективный принимается такой диаметр шарообразной частицы, который соответствует сумме масс всех фракций, начиная от нуля и кончая этим диамет­ром, равной 10%. Надо найти, кроме того, диаметр d_0, который соответствует сумме масс фракций,, равной 60%. Коэф­фициент однородности d_o/d_э должен быть не более 5 (d_o/d_э ≤ 5) и d_э должен лежать в пределах от 0,1 до 3 мм.

По способу Крюгера — Цункера используют данные механического анализа грунта и определяют d_э по формуле

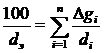(I.5)

Скоростью фильтрации w называется отношение объемного расхода жидкости к площади поперечного сечения пласта, нормального к направле­нию движения жидкости

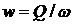(I.6)

Скорость фильтрации представ­ляет собой фиктивную скорость, с которой двигалась бы жидкость, если бы пористая среда отсутство­вала (m=1).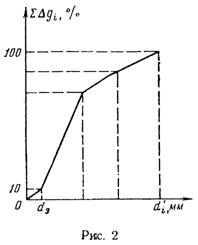

Средняя скорость движения жидкости v равна отношению объ­емного расхода к площади просве­тов ω_просв (живому сечению пото­ка)

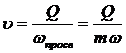(I.7)

Скорость фильтрации и средняя скорость движения связа­ны соотношением

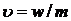
Критерий Рейнольдса

Подобно тому, как в трубной гидравлике критерием режи­ма движения служит число Рейнольдса

Re = υdρ/μ (II.1)

в теории фильтрации вводится безразмерный параметр

Re = 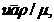(II. 2)

где и — некоторая характерная скорость; 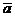— линейный пара­метр, характеризующий среднее сечение поровых каналов; ρ — плотность жидкости; μ — динамический коэффициент вяз­кости.

Скорость фильтрации, при которой нарушается закон Дарси, называется критической скоростью фильтра­ции (w_кр).

Однако нарушение линейного закона фильтрации еще не означает перехода от ламинарного движения к турбулентному. Закон Дарси нарушается вследствие того, что силы инерции, возникающие в жидкости за счет извилистости каналов и из­менения площади их поперечных сечений, становятся при w > w_кр соизмеримыми с силами трения.

В трубной гидравлике значение Re, при котором происхо­дит смена режимов, равно Re_кр= 2320, в теории фильтрации закон Дарси имеет место при значении безразмерного парамет­ра Re, меньшего критического (Re_кр), которое устанавливается из опыта.

Впервые число Рейнольдса для фильтрации жидкости было введено Н. Н. Павловским в виде

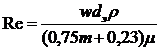(II.3)

т. е. за характерную скорость была взята скорость фильтрации w, а линейный параметр представлен выражением

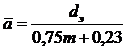(II.4)

Критические значения Re по Павловскому заключены в интервале

Re_кр = 7,5 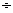9.

В. Н. Щелкачев предложил взять за линейный параметр выражение, пропорциональное корню квадратному из коэффи­циента проницаемости,

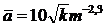(II.5)

Число Рейнольдса по В. Н. Щелкачеву имеет вид

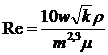(II.6)

a критические значения лежат в интервале

l ≤ Re_кр ≤ 12.

По М. Д. Миллионщикову за характерную скорость взята редкая скорость движения жидкости

υ = w/m,

аза линейный параметр — выражени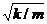е т. е.

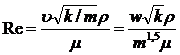(II.7)

Если вычисленное по одной из формул (II.З), (II.6), (II.7) значение числа Re оказывается меньше нижнего критического значения Re_кр, то закон Дарси справедлив, если Re больше верхнего значения Re_кр, то закон Дарси заведомо нарушен.

Широкий диапазон изменения Re_кр объясняется тем, что в формулы для числа Re входят параметры k и т, которые не полностью характеризуют микроструктуру породы. Как следует из опытов, для каждой горной породы можно указать более узкий диапазон значений Re_кр [16].

Определение режима фильтрации жидкостей и газов имеет большое практическое значение, ибо без знания закона фильт­рации в пласте нельзя правильно рассчитать дебиты скважин, распределение давления в пласте, а также невозможно опреде­ление параметров пласта (k, h, m и др.) по данным исследо­вания нефтяных и газовых скважин.

Формула Дюпюи

При плоскорадиальном движении векторы скорости фильт­рации направлены по радиусам к оси скважины, поэтому дав­ление и скорость фильтрации зависят только от одной коор­динаты r. При этом во всех горизонтальных плоскостях поле скоростей и давлений будет одинаковым.

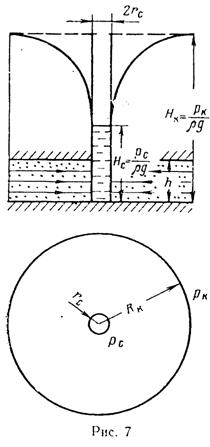
Примером плоскорадиального фильтрационного потока яв­ляется приток к гидродинамически совершенной скважине, покрывшей горизонтальный пласт бесконечной протяженности на всю мощность h и сообщающейся с пластом через пол­ностью открытую боковую поверхность цилиндра, отделяющую cтвол скважины от продуктивного пласта.

Поток будет также плоскорадиальным при притоке к со­вершенной скважине радиуса r_с (или оттоке от скважины), расположенной в центре ограниченного горизонтального цилиндрического пласта мощностью h и радиусом R_K (рис. 7).

Если на внешней границе пласта, совпадающей с контуром литания, поддерживается постоянное давление р_к, а на забое скважины постоянное давление p_с, пласт однороден по пори­стости и проницаемости, фильтрация происходит по закону Дарси, то объемный дебит скважины определится по формуле Дюпюи:

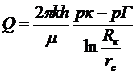(III.4)

где μ — динамический коэффициент вязкости.

Закон распределения давления определяется по одной из формул:

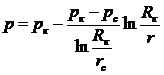(III.5)

либо

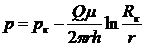
(III.6)

либо

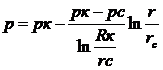(III.7)

Линия р=р(r) называется депрессионной кривой дав­ления. Характерно, что при при­ближении к скважине градиенты давления и скорости фильтрации резко возрастают. При построении карты изобар следует учитывать, что радиусы изобар изменяются в геометрической прогрессии, в то время, как давление на изобарах изменяется арифметической прогрессии.

Индикаторная линия — зависимость дебита скважины от депрессии Δр = р_к—р_с, при притоке к скважине в условиях справедливости закона Дарси представляет собой прямую ли­нию, определяемую уравнением Q=KΔp.

Коэффициент продуктивности

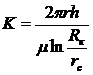(III.8)

численно равен дебиту при депрессии, равной единице.

Закон движения частиц вдоль линии тока, если при t = 0 частица находилась в точке с координатой r = r₀, описывается уравнением

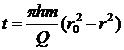(III.9)

или

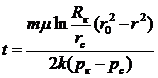(III.9a)

Средневзвешенное по объему порового пространства Ω пластовое давление

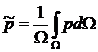
где

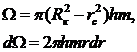
Подставляя выражение для p (III.5), выполняя интегрирование и пренебрегая всеми членами, содержащими r_c², полу­чим

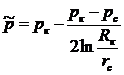(III.11)

Закон распределения давления и формула дебита при на­рушении закона Дарси при притоке к совершенной скважине получаются из двучленной формулы

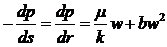(III.12)

Подставляя выражение для скорости фильтрации

w = Q/2πrh

в(III.12) и разделяя переменные, получим

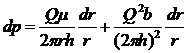(III.13)

Интегрируя по р в пределах от р_с до р_к и по r в пределах от r_с до R_k будем иметь

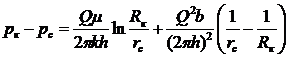(III.14)

Решая полученное квадратное уравнение, находим дебит скважины Q. Интегрируя (III.13) по р в пределах от р до р_к и по r в пределах от r до R_к, найдем закон распределения давления

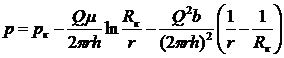(III.15)

Как видно из (III.14), индикаторная линия при нарушении закона Дарси является параболой.

Если фильтрация происходит по закону Краснопольского, то дебит определяется по формуле

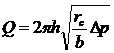(III. 16)

Жидкости по закону Дарси

Фильтрационный поток называется радиально-сферическим, «если векторы скорости фильтрации направлены в пространстве по прямым, радиально сходящимся к од­ной точке (или расходящимся от нее).

Благодаря центральной симметрии дав­ление и скорость фильтрации зависят и в этом случае только от одной координаты r, отсчитываемой от центра (рис. 8). При­мером потока, весьма близкого радиально-сферическому, является приток жидко­сти к гидродинамически несовершенной скважине малого диаметра, едва вскрыв­шей непроницаемую горизонтальную 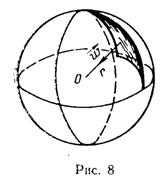кров­лю однородного пласта большой мощности (теоретически бесконечной). Если на забое скважины, представленной в виде полусферы радиуса r_с, поддерживается постоянное приведенное давление, 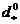, а на достаточно большом расстоянии от скважины, на полусферической поверхности радиуса R_к сохраняется посто­янное давление 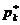и фильтрация в однородном пласте проис­ходит по закону Дарси, то объемный дебит скважины опреде­ляется по формуле

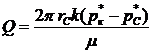(III.17)

Приведенное давление в любой точке пласта определяется по формуле

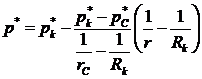(III.18)

азакон движения частиц вдоль линии тока от точки с координатой r₀ до точки с координатой r описывается уравнением

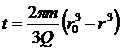(III.19)

Задача 20

Определить дебит дренажной галереи шириной B = 100 м, если мощность пласта h=10 м, расстояние до контура питания l = 10 км, коэффициент проницаемости пласта k=1 Д, динамический коэффициент вязкости жидкости μ = l сП, давление на контуре питания p_к = 9,8 МПа (100 кгс/см²) и давление в галерее p_г = 7,35 МПа (75 кгс/см²). Движение жидкости напорное, подчиняется закону Дарси.

Ответ: Q = 21,6 м³/сут.

Задача 21

Определить коэффициент проницаемости пласта (в различ­ных системах единиц), если известно, что в пласте происходит одномерное, прямолинейно-параллельное установившееся движение однородной жидкости по закону Дарси. Гидравлический уклон i = 0,03, ширина галереи В = 500 м, мощность пласта h=6 м, плотность жидкости ρ = 850 кг/м³, динамический коэф­фициент вязкости μ = 5 сП и дебит галереи Q = 30 м³/сут.

Ответ: k=2,27 Д=32∙10^-8 см²=2,32∙10^{-12 м2}.

Задача 22

Показать графически распределение давления и найти градиент давления при прямолинейно-параллельном движении в пласте несжимаемой жидкости по линейному закону фильтрации, используя следующие данные: длина пласта l_к = 5 км, мощность пласта h=10 м, ширина галереи B = 300 м, коэффи­циент проницаемости пласта k = 0,8 Д, давление в галерее р_г = 2,94 МПа (30 кгс/см²), динамический коэффициент вязкости жидкости μ = 4 сП, дебит галереи Q = 30 м³/сут.

Ответ: p = 5,78 - 0,0568∙10^-2х (х в м, р в МПа), - dp/dx = 0,0568∙10^-2 МПа/м.

Задача 23

Определить дебит нефтяной скважины (в т/сут) в случае установившейся плоскорадиальной фильтрации жидкости по закону Дарси, если известно, что давление на контуре питания р_к =9,8 МПа (100 кгс/см²), давление на забое скважины р_с =7,35 МПа (75 кгс/см²), коэффициент проницаемости пласта k = 0,5 Д, мощность пласта h = 15 м, диаметр скважины Dc=24,8 см, радиус контура питания R_к=10 км, динамический коэффициент вязкости жидкости μ = 6 мПа∙с и плотность жидкости р = 850 кг/м³.

Ответ: Q_m= 127 т/сут.

Задача 24

Определить давление на расстоянии 10 и 100 м от оси скважины при плоскорадиальном установившемся движении несжимаемой жидкости по линейному закону фильтрации, счи­тая, что коэффициент проницаемости пласта k = 0,5 Д, мощ­ность пласта h = 10 м, давление на забое скважины р_с = = 7,84 МПа (80 кгс/см²), радиус скважины r_с== 12,4см, дина­мический коэффициент вязкости нефти μ = 4∙10^-3 кг/м∙с, плотность нефти ρ = 870 кг/м³ и массовый дебит скважины Q_m = 200 т/сут.

Ответ: p₁=9,28 МПа; p₂ = 10,06 МПа.

Задача 25

Построить индикаторную линию (зависимость дебита Q от перепада давления Δр = р_к —р_с), имеющуюся при установив­шейся плоскорадиальной фильтрации жидкости по линейному закону, если известно, что давление на контуре питания p_к = 8,82 МПа (90 кгс/см²), коэффициент проницаемости пласта k = 600 мД, мощность пласта h=10 м, диаметр скважины D_c = = 24,8 см, расстояние от оси скважины до контура питания R_k=10 км и динамический коэффициент вязкости нефти μ = 5 мПа∙с.

Ответ: индикаторная линия — прямая, описываемая уравне­нием Q = 5,77 Δр (Q в м³/сут, Δр в кгс/см²).

Задача 26

Определить коэффициент гидропроводности пласта kh/μ по данным о коэффициенте продуктивности скважины. Извест­но, что фильтрация происходит по закону Дарси, коэффициент продуктивности K=18 т/сут (кгс/см²), среднее расстояние меж­ду скважинами 2σ = 1400 м, плотность ρ=925 кг/м³, радиус скважины r_с= 0,1 м.

Ответ:kh/μ = 3,18∙10^-9 м⁴∙с/кг (318 Д∙см/сП).

Задача 27

Определить средневзвешенное по объему пластовое давле­ние, если известно, что давление на контуре питания р_к = 9,8 МПа (100 кгс/см²), давление на забое возмущающей скважины p_с = 7,84 МПа (80 кгс/см²), расстояние до контура питания R_к = 25 км, радиус скважины r_с = 10 см. В пласте име­ет место установившееся плоскорадиальное движение несжи­маемой жидкости по закону Дарси.

Ответ: р = 9,72 МПа (99,19 кгс/см²).

Задача 28

Определить относительное понижение s_p/s= (H_к—Н)/(Н_к—H_с) пьезометрического уровня в реагирующих скважинах, расположенных от возмущающей скважины на расстояниях 1 м, 100 м, 1 км, 10 км. Движение жидкости установившееся плоскорадиальное по закону Дарси. Радиус скважины r_с = 0,1 м, расстояние до контура питания R_к=100 км.

Ответ: s_p/s равно соответственно 0,83; 0,50; 0,33; 0,167.

Задача 29

Определить время отбора нефти из призабойной зоны скважины радиусом r₀=100 м, если мощность пласта h=10 м, коэффициент пористости пласта m = 20%, массовый дебит нефти Q_m =40 т/сут, плотность ее ρ= 920 кг/м³, r_с = 0,1 м.

Ответ: Т = 1440 сут.

Задача 30

Определить время t, за которое частица жидкости подойдет к стенке скважины с расстояния r₀ = 200 м, если коэффициент проницаемости пласта k=1 Д, динамический коэффициент вяз­кости нефти μ = 5 сП, депрессия во всем пласте радиусом R_к = 1 км составляет р_к—р_с= 10 кгс/см²; мощность пласта h=10м, коэффициент пористости пласта m = 15%, радиус скважины r_c = 10 см.

Ответ: t = 1600 сут.

Задача 31

Как изменится дебит скважины Q при увеличении радиуса скважины вдвое?

1. Движение происходит по линейному закону фильтрации.

2. Фильтрация происходит по закону Краснопольского.

Начальный радиус скважины r_с = 0,1 м. Расстояние до контуpa питания R_к = 5 км.

Ответ: 1) Q’: Q=l,07; 2) Q’: Q= 1,41, т. е. при движении жидкости по линейному закону фильтрации влияние изменения радиуса скважины менее интенсивно, чем при движении по закону Краснопольского.

Задача 32

Найти изменение перепада давления Δр при увеличении радиуса скважины вдвое, при котором дебит остается прежним. Рассмотреть два случая, как в предыдущей задаче. Начальный радиус скважины r_с = 0,1 м, расстояние до контура питания R_к= 1 км.

Ответ: 1) Δр'/Δр = 0,925, 2) Δр'/Δр = 0,5.

Задача 33

Во сколько раз необходимо увеличить радиус скважины, чтобы дебит ее при прочих равных условиях удвоился?

1) Движение жидкости происходит по закону Дарси.

2) Жидкость фильтруется по закону Краснопольского. На­чальный радиус скважины r_с = 0,1 м. Расстояние до контура питания R_к= 1 км.

Ответ: 1) n=100, r'_c=10 м; 2) n = 4, r'_с = 0,4 м.

Задача 34

Скважина радиусом r_с=10 см расположена в центре круго­вого пласта радиусом R_к = 350 м. Коэффициент проницаемости пласта k = 0,8 Д, мощность h=12м, динамический коэффициент вязко­сти нефти μ=5 сП. Определить дебит скважины, считая, что за­лежь по контуру радиуса R_к ча­стично непроницаема (рис. 9). Кон­тур питания представляет собой в плане дугу окружности радиусом R_к с центральным углом α = 120°. Давление на контуре питания р_к = 27,9 МПа (285 кгс/см²), давление на забое скважины р_с = 7,84 МПа (80 кгс/см²).

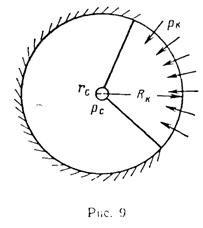Решение. Задачу можно свести к плоскорадиальной, если в форму­ле Дюпюи за контурное давление принять средневзвешенное по длине окружности давление р_к

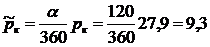МПа,

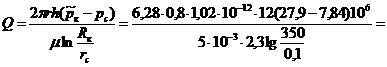
= 2,22-10~³ м³/с - 192 м³/сут.

Задача 35

Сколько жидкости следует закачивать в пласт в единицу времени через нагнетательную скважину, если необходимо, чтобы давление в скважине поддерживалось в процессе за­качки на Δр=1,47 МПа (15 кгс/см²) выше давления, устано­вившегося в пласте на расстоянии r = 2 км от скважины? Имеет место закон Дарси. Динамический коэффициент вязко­сти μ =1 сП, коэффициент проницаемости пласта k = l50 мД, мощность пласта h =10 м, радиус скважины r_с = 10 см.

Ответ: Q=123 м³/сут.

Задача 36

Определить приведенное давление в точках, отстоящих на r = 20 м, 10 м, 5 м, 1,5 м, 1 м от центра забоя скважины, вскрывшей пласт бесконечной мощности на величину b = 0,5 м. На расстоянии R_к=1000м приведенное давление р_к*= 9,8 МПа (100 кгс/см²), на забое скважины р_с*=7,35 МПа (75кгс/см²), рллиус скважины r'_c = 12,4см. Фильтрация к скважине происходит по закону Дарси.

Указание.Представляя забой скважины в виде полусферы, Равновеликой по площади забою действительной скважины, определить радиус полусферы r_c(2πr'_сb=2πr²_c).

Ответ: соответственно р* = 9,77; 9,74; 9,68; 9,39; 9,19 МПа.

Задача 37

Скважина вскрывает пласт бесконечно большой мощности на небольшую глубину. Считая движение радиальносферическим, определить время перемещения частиц жидкости вдоль линий тока от точки с координатой r₀=100 м до точки с коор­динатой r = 5 м. Скважина эксплуатируется с постоянным дебитом Q = 120м³/сут, коэффициент пористости пласта m = 15%.

Ответ: t = 7,15 лет.

СВЯЗЬ ПЛОСКОЙ ЗАДАЧИ ТЕОРИИ

КОМПЛЕКСНОГО ПЕРЕМЕННОГО

В самом общем случае давление и скорость фильтрации за­висят от трех координат точки в пласте. Если давление и ско­рость фильтрации зависят только от двух координат, то в каждой плоскости, перпендикулярной к третьей оси, поле ско­ростей и давлений будет одинаковым. В этом случае фильтра­ционный поток называется плоским. Плоский фильтрационный поток имеет место при работе одной или нескольких гидроди­намически совершенных (эксплуатационных и нагнетательных) скважин в однородном горизонтальном пласте постоянной мощ­ности. Именно такие потоки будут рассмотрены в настоящем разделе.

Принцип суперпозиции

Назовем точечным стоком па плоскости точку, поглощаю­щую жидкость. Сток можно рассматривать как гидродинами­чески совершенную эксплуатационную скважину бесконечно малого радиуса в пласте единичной мощности. Точечный источ­ник — это точка, выделяющая жидкость (аналог нагнетатель­ной скважины). Заменяя источники и стоки скважинами ко­нечного диаметра, мы практически не допускаем никакой ошибки, поэтому будем в дальнейшем отождествлять скважины с источниками и стоками.

При работе в бесконечном пласте одной скважины-стока фильтрация будет плоскорадиальной и давление в точке на расстоянии rот центра скважины определяется по формуле

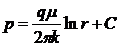(IV.1)

где q=Q/h — дебит скважины-стока, приходящийся на едини­цу мощности пласта; С — постоянная интегрирования.

Назовем потенциалом скорости фильтрации Ф выражение Ф = kp/μ. Переходя от давления к потенциалу, получим значе­ние потенциала в точке на расстоянии rот центра скважины

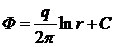(IV.2)

Дебиту источника (нагнетательной скважины) приписыва­ется знак минус.

При совместной работе в пласте нескольких скважин ре­зультирующий потенциал в любой точке пласта М равен ал­гебраической сумме потенциалов Ф₁, Ф₂, ... , обусловленных работой каждой отдельной скважины.

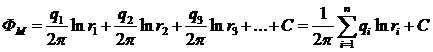(IV.3)

Скорости фильтрации при этом складываются геометрически (рис. 10, а, б). Это называется принципом суперпозиции или сложения течений.

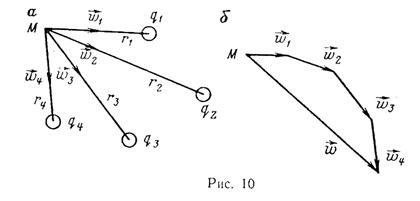
Используя принцип суперпозиции, можно приближенно рас­считывать дебиты или забойные потенциалы (а следовательно, и забойные давления) для группы скважин, работающих в пласте с весьма удаленным контуром питания. Потенциал Ф_к на контуре питания считается известным, а расстояние от контура питания до всех скважин — одно и то же и приблизитель­но равно R_к.

Помещая мысленно точку М последовательно на забой каждой скважины, где Ф_м = Ф_сi, получим из общего уравнения (IV.3) систему п уравнений (п — число скважин). Постоянная интегрирования находится из условия на контуре питания. Окончательно система уравнений для определения дебитов или забойных потенциалов примет вид

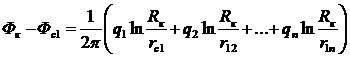(IV.4)

…………………………………………………………

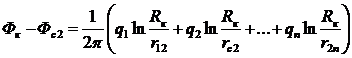
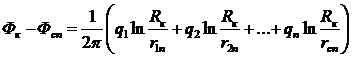
здесь r_ij — расстояние между центрами i-той и j-той скважин.

Принцип суперпозиции можно использовать, если скважины работают в пласте, ограниченном контуром питания той или мной формы, или непроницаемыми границами (линии выклинивания, сбросы), но для выполнения тех или иных условий на границах приходится вводить фиктивные скважины за преде­лами пласта, которые создают в совокупности с реальными скважинами необходимые условия на границах.

При этом задача сводится к рассмотрению одновременной работы реальных и фиктивных скважин в неограниченном пласте. Этот метод называется методом отображения источни­ков и стоков. Он широко применяется не только в подземной гидравлике и гидродинамике, но и при решении задач теории электричества, магнетизма и электропроводности.

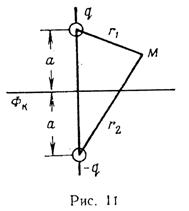Так, если эксплуатационная скважи­на находится в пласте с прямолинейным контуром питания на расстоянии а от контура, то ее надо зеркально отобра­зить относительно контура, т. е. поме­стить фиктивную скважину с другой сто­роны от контура на расстоянии а (рис. 11) и считать ее дебит отрицательным (скважина — источник). При этом потенциал в любой точке М равен

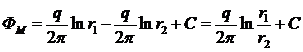
на контуре питания r₁ = r₂ и Ф = С=Ф_к, а дебит скважины определяется по формуле

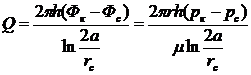(IV.5)

Метод отображения источников и стоков используется так­же в задачах 52, 53 для нахождения дебита скважины, рабо­тающей в пласте, ограниченном пересекающимися прямолиней­ными непроницаемыми границами. При помощи этого метода можно определить дебит скважины, эксцентрично расположен­ной в круговом пласте

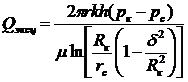(IV.6)

где δ — расстояние от центра скважины до центра кругового пласта (эксцентриситет).

Интерференция скважин

Дебит каждой скважины бесконечной цепочки, расположен­ной на расстоянии L от прямолинейного контура питания (рис. 12), выражается формулой

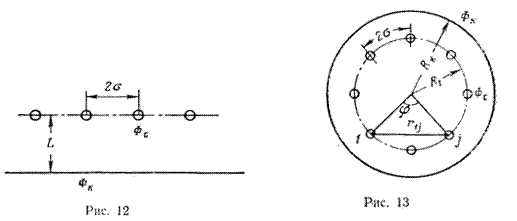
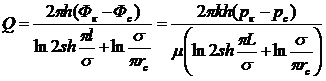(IV.7)

где σ - половина расстояния между скважинами. Если L ≥ σ, то приближенно можно принять, что

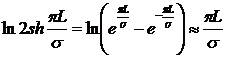
и тогда

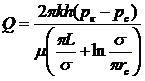(IV.8)

Дебит одной скважины кольцевой батареи, состоящей из п скважин, в круговом пласте радиуса R_к (рис. 13) имеет вид

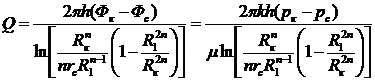
где R₁ — радиус батареи; r_с — радиус скважин.

Если число скважин батареи велико (больше пяти или ше­сти), то (R₁/R_к)²ⁿ ≤ 1 и этим выражением можно пренебречь по сравнению с единицей; если, кроме того, заменить

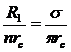то получим приближенную формулу

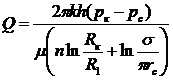(IV. 10)

Формулы (IV.7) и (IV.9) можно вывести, используя метод отображения.

Если в пласте эллипти­ческой формы работает п равноотстоящих друг от друга скважин (рис. 14), то дебит одной скважины определяется по формуле, предло­женной В. Т. Мироненко [11] 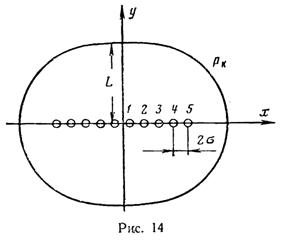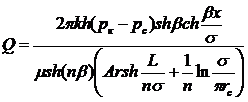(IV.11)

где β находится из уравнения

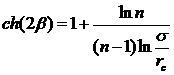(IV. 12).

х — координата центра скважины; L — малая полуось эллипса; σ — половина расстояния между скважинами.

§ 3. Метод эквивалентных фильтрационных сопротивлений

Одним из методов расчета дебитов многорядных батарей или цепочек скважин является метод эквивалентных фильтра­ционных сопротивлений Ю. П. Борисова.

Суммарный дебит цепочки из п скважин равен

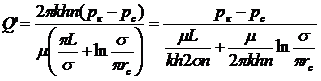(IV.13)

Используя электрогидродинамическую аналогию и учиты­вая, что аналогом объемного расхода является сила тока, а аналогом разности давлений — разность электрических потен­циалов, выражение, стоящее в знаменателе, можно назвать фильтрационным сопротивлением. Оно складывается из внеш­него фильтрационного сопротивления

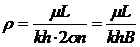(IV.14)

которое представляет собой сопротивление потоку от контура питания до галереи длиной В = 2σп, расположенной на рас­стоянии L от контура питания, и из внутреннего фильтрацион­ного сопротивления

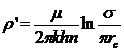(IV. 15)

которое выражает собой сопротивление, возникающее при под­ходе жидкости к скважинам в зоне радиуса σ/π, где фильтра­ция практически плоскорадиальная.

Формула (IV. 13) примет вид

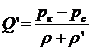(IV.16)

Электрическая схема, соответствующая последней формуле, представляет собой два последовательно соединенных провод­ника с сопротивлениями ρ и ρ', с разностью потенциалов p_к и p_c и силой тока Q' (рис. 15).

Если в пласте имеется три цепочки с