Перечень экзаменационных (зачетных) вопросов.
1. Предмет эконометрики. Методология эконометрического исследова- ния.
2. Типы моделей. Спецификации моделей.
3. Типы экономических данных.
4. Модель парной регрессии.
5. Параметры, характеризующие качество линейной модели.
6. Метод наименьших квадратов в регрессионном анализе.
7. Линейная модель регрессии.
8. Выражение параметров линейной модели регрессии через средние значения исходных данных.
9. Статистические характеристики оценок параметров парной линейной регрессии.
10. Теорема Гаусса-Маркова.
11. Проверка значимости параметров линейной модели.
12. Проверка значимости линейной модели в целом.
13. Нелинейная регрессия и ее классификация.
14. Варианты сведения нелинейной регрессии к линейной.
15. Оценка параметров линейной регрессии и коэффициента корреляции.
16. Прогнозирование в случае линейной модели регрессии, интервальные
оценки.
17. Доверительные интервалы прогнозируемых значений линейной моде- ли.
18. Варианты получения доверительных интервалов прогнозируемых значений и их характеристика.
19. Корреляция для нелинейной модели регрессии
20. Средняя ошибка аппроксимации.
21. Статистическая характеристика корреляции нелинейной модели регрессии .
22. Множественная линейная регрессия в скалярной и векторной формах.
23. Выбор структуры уравнения множественной регрессии.
24. Оценка параметров уравнения множественной регрессии.
25. Временные ряды, основные элементы временного ряда.
26. Автокорреляция уровней временного ряда и выявление его структуры.
27. Моделирование тенденции временного ряда.
28. Аддитивная модель временного ряда.
29. Мультипликативная модель временного ряда.
30. Моделирование сезонных и циклических колебаний временных рядов.
31. Метод скользящей средней в моделировании временных рядов.
32. Метод фиктивных переменных в моделировании сезонных колебаний
временных рядов.
33. Моделирование тенденции временного ряда при наличии структурных изменений.
34. Модели временных рядов и методика оценки их качества.
35. Временные ряды и прогнозирование.
36. Доверительные интервалы для прогнозируемых значений временных рядов.
37. Тест Чоу, его особенности.
38. Мультиколлинеарность данных.
Тесты.
1. В парной регрессии выбор вида математической функции может быть осуществлен:
1. Графическим методом.
2. Аналитическими методом.
3. Экспериментальным методом.
4. Перечисленными в п.1-3 методами.
2. Коэффициент линейной корреляции r 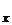 должен удовлетворять условию:
должен удовлетворять условию:
1. -1 
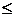 r
r 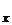
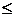 1 ;
1 ;
2. 0 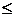 r
r 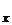
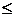 1 ;
1 ;
3. -1< r 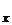 < 1 ;
< 1 ;
4. 0 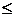 r
r 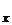 < 1 ;
< 1 ;
3. Коэффициент детерминации R 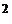 должен удовлетворять условию:
должен удовлетворять условию:
1. 0 < R 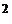 <1 ;
<1 ;
2. 0 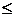 R
R 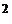 < 1 ;
< 1 ;
3. 0 < R 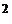
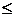 1
1
4. -1 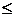 R
R 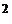
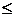 1 ;
1 ;
4. Различают следующие классы нелинейных регрессий:
1. Регрессии, нелинейные относительно включенных
в нее объясняющих переменных, но линейные по оцениваемым параметрам.
2. Регрессии, нелинейные по оцениваемым параметрам.
3. Регрессии, нелинейные по объясняющим переменным и оцениваемым параметрам.
4. В классификацию входят пункты ответов 1 и 2.
5. Регрессия, нелинейная относительно объясняющей переменной, но линейная по оцениваемым параметрам, является:
1. y 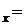 a+b
a+b 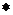 x
x 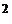 ;
;
2. y 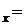 a
a 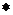 x
x 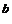 ;
;
3. y 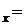 a+b
a+b 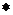 lnx ;
lnx ;
4. Пункты 1 и 3.
6. Качество линейной модели регрессии характеризуется только:
1. Коэффициентом корреляции r 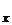 ;
;
2. Коэффициентом детерминации R 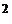 ;
;
3. Средней ошибкой аппроксимации 
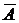
 ;
;
4. Перечисленными в пунктах 1,2,3 параметрами.
7. Индекс детерминации применяется для оценки качества:
1. Линейной модели регрессии;
2. Нелинейной модели, но сводимой к линейной модели регрессии;
3. Нелинейной модели регрессии;
4. Перечисленных в пунктах 1 и 2 случаях.
8. Наиболее точно качество линейной модели регрессии характеризует:
1. Коэффициент корреляции;
2. Коэффициент детерминации;
3. Средняя ошибка аппроксимации;
4. Перечисленные в пунктах 1 и 3 параметры.
9. Исходные данные в эконометрике подразделяют на следующие категории:
1. Пространственные;
2. Временные;
3. Случайные;
4. Перечисленные в пунктах 1 и 2 вариантах.
10. Автокорреляционная функция используется для :
1. Выявления структуры временного ряда;
2. Выявления количества объясняющих переменных в модели;
3. Выявления во временном ряде наличия или отсутствия трендовой и циклической компонент;
4. Перечисленных в пунктах 1 и 3 вариантов.
11. Аддитивная модель временного ряда имеет следующий вид:
1. Y=T+S 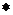 E ;
E ;
2. Y=T 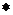 E +S ;
E +S ;
3. Y=T 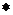 E
E 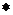 S ;
S ;
4. Y= T+E+S .
12. Мультипликативная модель временного ряда имеет следующий вид:
1. Y=T+S+E ;
2. Y=S 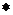 E+T ;
E+T ;
3. Y= S+T 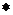 E ;
E ;
4. Y=S 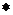 E
E 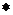 T .
T .
13. Для моделирования циклических компонент во временном ряде применяется только:
1. Метод скользящей средней ;
2. Метод фиктивных переменных;
3. Метод комплексных оценок;
4. Перечисленные в пунктах 1 и 2 методы.
14. Тест Чоу применяется для:
1. Моделирования тенденции временного ряда при наличии структурных изменений;
2. Моделирования циклической компоненты;
3. Моделирования трендовой компоненты;
4. Моделирования случайной компоненты.
15. При наличии в исходных данных аномальных значений, рекомендуется:
1. Исключить их при построении модели;
2. Не исключать их при построении модели;
3. Корректировать аномальные значения;
4. Выполнить рекомендации указанные в пунктах 2 и 3.
Список литературы.
1. Магнус Я.П., Катышева П.К., Пересецкий А.А. Эконометрика. Начальный курс. М.: Дело, 1998.-248с.
2. Кулинич Е.И. Эконометрика. – М.: Финансы и статистика, 1999.-304с.
3. Елисеева И.И. Эконометрика.- М.: Финансы и статистика, 2002.-344с.: ил.
4. Четыркин Е.М., Калихмен И.Л. Вероятность и статистика. М.: Финан- сы и статистика, 1982с.
5. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики: Учебник.- М.: ЮНИТИ, 1998.
6. Доугерти К. Введение в эконометрику.- М.: Финансы и статистика, 1999.
7. Кейн Э. Экономическая статистика и эконометрия. Введение в количественный экономический анализ.- М.: Статистика, 1977.- Вып. 1.
8. Маленво Э. Статистические методы эконометрики.- М.: Статистика, 1976.
9. Фишер Ф. Проблемы идентификации в эконометрии.- М.: Статистика, 1978.
11. Кремер Н.М., Путко Б.А. Эконометрика.- М.: ЮНИТИ-ДАНА, 2006.
10. Федосеев В.В. Гармаш А.Н. и др. Экономико-математические методы и прикладные модели.- 2-е изд. Перераб. И доп. – М.: ЮНИТИ-ДАНА,
2005.
12. Пинегина М.В. Математические методы и модели в экономике.- М.: «Экзамен», 2004.
13. Катышев П.К., Пересецкий А.А. Сборник задач к начальному курсу эконометрики. М.: Дело, 1999.-72с.
14. Магнус Я.Р., Катин П.Н. Сборник задач по эконометрике.
15. Елисеева И.И. Практикум по эконометрике.-М.: Финансы и статистика, 2003.-192 с.: ил.
16. Елисеева И.И., Юзбашев М.М. Общая теория статистики.-4-е изд., перераб. и доп.- М.: Финансы и статистика,2001.
17. Тинтнер Г. Введение в эконометрию.- М.: Финансы и статистика, 1965.
18. Четыркин Е.М. Статистические методы прогнозирования.- М.: Статистика, 1977.
19. Методические материалы по экономическим дисциплинам для преподавателей средних школ и вузов/ Под общ. ред. Л.С. Гребнева. Экономическая статистика. Эконометрика. (программы, тесты, задачи, решения). М.: ГУ-ВШЭ, 2000. –112с.
20. Лизер С. Эконометрические методы и задачи.- М.: Статистика, 1971.
В.В. Матвеева, А.А. Малов
ЭКОНОМЕТРИКА
УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС
для студентов специальностей «Бухгалтерский учет, анализ и аудит», «Финансы и кредит»
Филиал Российского государственного социального университета в г. Чебоксары 428027, г. Чебоксары, ул. Хузангая, 20
Отпечатано в фирме «Альбион» в форме ООО.
428027, г. Чебоксары, ул. Хузангая, 14 офис 213
Формат 60/84/16. Бумага газетная. Печать оперативная.
Усл. печ. л. 3,0. Уч. –изд. л. 1,6. Тираж 50 экз.
Заказ №101.
Подписано к печати 04,04.2008 г.
