Взаимодействие скважин при нестационарных процессах

Метод суперпозиции фильтрационных потоков используется и в задачах неустановившихся процессов при упругом режиме.

Группа скважин. Так, если в пласте действует группа скважин, в числе которых имеются как эксплуатационные, так и нагнетательные скважины, понижение давления в какой-либо точке пласта Dр определяется сложением понижений давлений, создаваемых в этой точке отдельными источниками и стоками, изображающими скважины Dр_j. Следовательно,

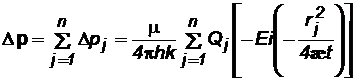, (7.29)

где n–число скважин;Q_j – объемный дебит стока (+) или источника(-) за номером j; r_j– расстояние данной точки пласта от скважины за номером j.

Так как аргумент интегрально-показательной функции мал (меньше 1), то зависимость (7.29) можно переписать в виде

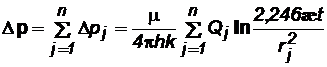. (7.30)

Данная зависимость используется для расчета параметров пласта путем обработки кривой восстановления давления в случае скважины, эксплуатирующейся в течение длительного времени и остановленной для исследования.

Периодически работающая скважина. В неограниченном пласте останавливается скважина, эксплуатирующаяся с постоянным дебитом Qв течении времениТ,сравнимого со временем проведения исследований. Понижение давления Dр^/ в момент времени Тможно найти по формуле (7.23). С момента остановки давление в ней и окружающей области пласта повышается, т.е. с данного момента в одном и том же месте пласта как бы действуют совместно и непрерывно эксплуатационная (сток) и нагнетательная (источник) скважины. При этом источник имеет тот же дебит Q. Обозначим повышение давления за счет работы источника через Dр^//. Таким образом, начиная с момента времени Т, на основании формулы (7.23) имеем:

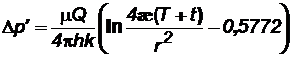, (7.31)

.

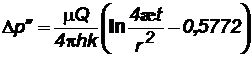Результирующее понижение давления Dр в любой точке пласта находится по методу суперпозиции

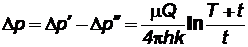. (7.32)

Обозначая через р_сдавление на забое скважины после её остановки, получаем

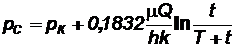. (7.33)

Зависимость (7.33) используется при гидродинамических исследованиях скважин, работающих не продолжительное время, методом построения кривой восстановления давления.

Решение плоских задач фильтрации методами теории функций комплексного переменного

Общие положения теории функций комплексного переменного

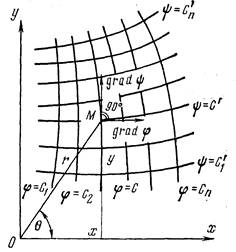
Рис. 7.19. Ортогональность изобар и линий тока

Круг задач, рассмотренных в предыдущем разделе, может быть значительно расширен, если к решениям применить аппарат теории функций комплексного переменного. При этом оказывается возможным исследовать отдельные вопросы плоского потока более полно. Рассмотрим связь между задачами плоского фильтрационного потока и теорией функций комплексного переменного.

Совместим с основной плоскостью течения плоскость комплексного переменного z = х + iy.Каждое комплексное число z изображается в этой плоскости точкой М (х, у) (рис. 7.19.). Функцией комплексного переменного z будет комплексное переменное F (z), если указан закон, позволяющий получить значение F (z) no заданному значению z.

Отделив в функции F (z) действительную часть от мнимой, можем записать

F (z) = F (х + iy) = j (х, у) + iy (х, у),(7.34)

где j(х, у) и y(х, у)-некоторые функции действительных переменных х и у; i – мнимая единица.

Задать функцию комплексного переменного - значит задать соответствие между парами чисел (х, у) и (j, y). Функция F (z) является аналитической в точке z_m,то есть имеющей производную во всех точках некоторой окрестности z_m.

В теории функций комплексного переменного имеются следующие положения:

7. Каждые две кривые, из которых одна принадлежит семейству кривых, определяемых уравнением j(х, у) = С, а другая - семейству кривых y(х, у) = С^* (С и С^* – постоянные), пересекаются под прямым углом, т. е. два семейства кривых образуют ортогональную сетку в основной плоскости течения.

2. Функции j(х, у)и y(х, у)удовлетворяют уравнению Лапласа, то есть

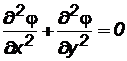; (7.35)

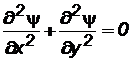. (7.36)

Положения 1 и 2 справедливы, если выполняются такие условия:

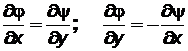. (7.37)

Условия (7.37) называются уравнениями Коши – Римана.