Вычислить значение функции используя формулу малых приращений

Пример 10.1. Вычислить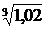

► Рассмотрим функцию y = 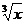. Вычислим ее производную в точке x = 1: y`(1) = 1/3.

По формуле малых приращений имеем (Dx = 0,02):

◄

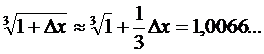Пример 10.2. Вычислить sin 29⁰

► Рассмотрим функцию y = sinx. Ее производная в точке x = p/6 = 30⁰ равна 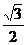. Тогда по формуле малых приращений получим (Dx =-p/180)

sin29 = sin(p/6-p/180) » sinp/6 – 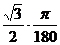= 1/2(1 – 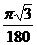) = 0,484 … .◄

1) sin60015' 2) cos60015' 3) tg60015' 4) ctg60015'

5) 20.013' 6) 50.012 7) 90.501 8) 2.013

9) 5.012 10) 91/3 11) 801/4 12) 1001/8

13) 10001/11 14) lg11 15) arctg1.05 16) sin46

17) cos 44 18) (7.01)³ 19) (7.01)⁴ 20) (7.01)⁷

21) arcsin0.99 22) arccos0.09 23) cos29 24) tg44

25) ctg46 26) arctg0.99 27) 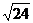28)

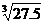
29) 16^0.503 30) sin14.5cos14.5

11. Найти уравнение касательной к графику функции y=f(x) в точке с абсциссой x₀ . Сколько общих точек имеет график данной функции с искомой касательной

Пример 11.1. y = x²/2 x₀ = 0

► y`=x по формуле уравнения касательной получим y = 0 + 0 = 0 Þ y = 0.

Найдем точки пересечения графика функции и касательной

x²/2 = 0 Þ x = 0 единственная точка совпадения графика функции с касательной – точка (0,0).◄

Пример 11.2.y = sinx, x₀ = p/2.

►y`=cosx, y(x<sub>0</sub>)=1, y`(x₀) = 0. Запишем уравнение касательной y = 1. Таким образом в точках пересечения графика функции и касательной получаем уравнение

sinx = 1 Þ x = p/2+2pk, kÎZ.

То есть, график функции имеет бесконечное число общих точек со своей касательной. Легче было решить эту задачу графически, так как, очевидно, что прямая y =1 будет касаться графика y = sinx во всех его «верхних» точках, а таких точек на всей числовой оси бесконечно много. ◄

1) y = sin3x +2, при x₀ = 0. 2) y = cos5px +6 , при x₀ = 1

3) y = sin5(x - 2) , при x₀ = 2 4) y = cos5px +8 , при x₀ = 1

5) y = tgpx +2, при x₀ = 1 6) y= ctg(px/2) +2, при x₀ =1

7) y = arctg2x +4 , при x₀ = 1 8) y= arcctg3x +6, при x₀ = 1/6

9) y = ax2+bx +c, при x₀ = –b/(2a) 10) y = ax+b, при x₀ = –b/(2a)

11) y = 1/x2, при x₀ = –1 12) y = x3+bx +c, при x₀ = 0

13) y = (x+1)/(x-1), при x₀ = –1/2 14) y = x2/(1+x), при x₀ = –1

15) y = (x+1)/(3-x)1/3, при x₀ = 2 16) y = sin4x – 1 , при x₀ = p/8

17) y = sin2(x - 1), при x₀ = 3 18) y = cos2x +3 , при x₀ = 0

19) y = tg4px +2, при x₀ = 1 20) y= ctg(3px/2) +2, при x₀ = 1

21) y = arctgx/2 +1, при, x₀ = 1 22) y= arcctg3x/4 +6, при x₀ = 1/8

23) y = 3/2x2, при x₀ = 7/2 24) y = x2+5x +23/24, при x₀ = 5/4

25) y = (2x+3)/(7x-15), при x₀ = 7/5 26) y = x4/2(4+2x), при x₀ = 1/2

27) y = tg46x –1/e, при x₀ = 2e 28) y = ctg(3x/8) -5, при x₀ = 1

29) y = (3x+9)/(6-2x)1/5, при x₀ =–2/3 30) y = sin4x/11 – 2 , при x₀ = 11p/8

12. Найти k-ю производную от функции y = f(x)

Пример 12.1. y=ax^-m, k=3

► Последовательно дифференцируя, имеем:

y` = –max^-m-1;

y`` = –ma(x^-m-1)` = am(m+1)x^-m-2;

y``` = am(m+1)(x^-m-2)`= –am(m+1)(m+2)x^-m-3◄

Пример 12.2. y= 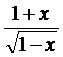, k = 100.

► Преобразуем данную функцию к удобному для дифференцирования виду

y = 2(1-x)^-1/2-(1-x)^1/2

После 100-кратного дифференцирования получаем:

◄

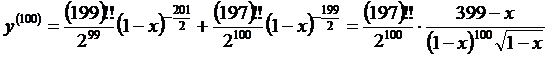1) k = 38, y = xex 2) k = 45, y = ex2

3) k = 30, y = sinx +ex 4) k = 39, y = cosx+ex

5) k = 68, y = cos2x +ex 6) k = 100, y = ln2x +ex

7) k = 50, y = 2x+ex 8) k = 618, y = (3x)121+ex

9) k = 63, y = 1+ex 10) k = 87, y = +ex+1/(x+1)

11) k = 88, y = 1/(1-x2)+ex 12) k = 98, y = 1/x+ex

13) k = 78, y = 756x8+56x6+ex 14) k = 6, y = 1+cos(x)ex

15) k = 5, y = +sin(x)ex 16) k = 6, y = x(2x–1)²(x+3)³

17) k = 3, y = 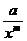18) k = 100, y =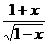

19) k = 20, y = x²e^2x 20) k = 10, y =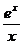

21) k = 6, y = sin²xlnx 22) k =100, y = xshx

23) k = 10, y = sinxsin2xsin3x 24) k = 50, y = x²sin2x

25) k = 5, y = xlnx 26) k = 5, y =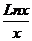

27) k = 8, y = 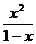28) k = 10, y =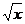

29) k = 6, y = cosxchx 30) k = 10, y = (2x–1)2^3x3^2x

13. С помощью правила ЛОПИТАЛЯ найти предел функции y =f(x) при x x₀ .

Пример 13.1.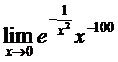

►Непосредственное применение правила Лопиталя не эффективно, поэтому, произведя замену 1/x² = y и применив правило Лопиталя к полученному выражению получим

◄

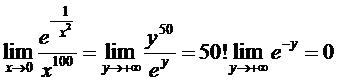Пример 13.2.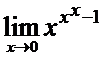

► Здесь имеется неопределенность вида 0⁰, поэтому предварительно воспользуемся представлением 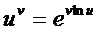(u>0, v>0), а также соотношением 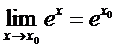, вытекающим из непрерывности функции e^x.

После очевидных преобразований и применения правила Лопиталя получаем

◄

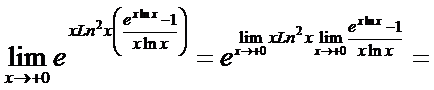
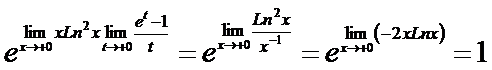1) x₀ = +0 y = xx. 2) x₀ = a y = (ax–xa)/(x–a)

3) x₀ = п/2 y = tg(3x)/tgx . 4) x₀ = 0 y = (tg(x)–x)/(x–sinx) .

5) x₀ = 0 y = sinax/sinbx . 6) x₀ =1 y = x1/(1–x).

7) x₀ = +0 y = (ln(1/x))x. 8) x₀ = 0 y = xalnx (a>0).

9) x₀ = 0 y = ((1+x)1/x-e)/x . 10) x₀ = 0 y = (1-cos(x2))/(x2sin(x2)) .

11) x₀ =¥ y = lnx/xa(a>0) . 12) x₀ = 0 y = sinax/tgbx .

13) x₀=0 y = ln(sin(ax))/ln(sin(bx)) . 14) x₀ = 0 y = ln(cos(bx))/ln(cos(ax))

15) x₀ = 0 y = (cos(sinx))-cosx)/x4. 16) x₀ = 0 y =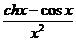

17) x₀=0 y= 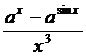18) x₀ = 1 – 0 y = lnx×ln(1-x)

19) x₀=0 y= 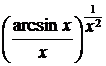20) x₀ ® +¥ y = (thx)^x

21) x₀ = 0 y = 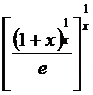22) x₀ = 0 y =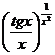

23) x₀ = 0 y = 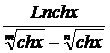24) x₀ = 0 y =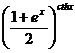

25) x₀ = 0 y = 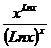26) x₀ = 0 y =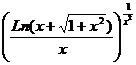

27) x₀ = 1 y = 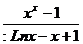28) x₀ = 0 y =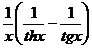

29) x₀ = +0 y = 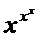-1 30) x₀ = p/4 y = (tgx)^tg2x

14.Найти второй дифференциал функции y = f(x) определяемой уравнением

Пример 14.1. y=lnx

► Находим последовательно

dy = – dx/x;

◄

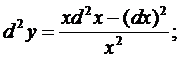
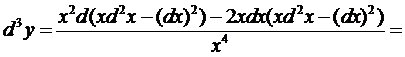
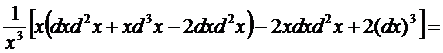
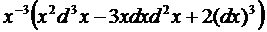Пример 14.2. y = f(x) , где x – функция от некоторой независимой переменной.

► Исходя из определения дифференциалов высших порядков, имеем:

dy = f`dx; d<sup>2</sup>y = d(f`dx) = f``(dx)² + f`d²x;

d³y = d(f``(dx)² + f`d²x) =

f```(dx)<sup>3</sup> + 2f``dxd<sup>2</sup>x + f``dxd<sup>2</sup>x + f`d<sup>3</sup>x = f```(dx)³ + 3d²xdxf`` + f`d³x.◄

1) sin(x + y) =y 2) tg(x + y) = y

3) exy + x + y = 0 4) log3(x + y) = x + y

5) log4(x2 + y) = 1-y 6) arccos(3x4 + y2) = y

7) (1 + x2 + y2)1/3= x-y2 8) arctg(x4 + 3y) = x + y6

9) arcctg(x5 + 2y) = x + y3 10) 2xy + y= xy + x

11) 31/(x + y)= xy 12) xy= x + y

13) yx = x2 + y3 14) (x + y)(x + y) = x4 + y7

15) logxy = x+y2 16) sin2(x + y) = 3y

17) log_xy = (x+y)² 18) 3^{x + y} + 2x + 5y = 0

19) y³ = x³ + 3y 20) arctg(x – y) = x + y

21) x^2y = x^x 22) ln(2x + 3y) = x – 2y²

23) 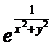= x²-y² 24) cos(xy) = sin(x + y)

25) tg(cosxy) = lnx³ 26) (x + y)³ = xy

27) log_3xx + y = y² 28) 2^{x + y} = x^y

29) lncos(x³ + y) = x + y⁵ 30) x^3x + y³ = 2xy

15. Построить с помощью элементарных преобразований графики функций

1.	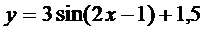2.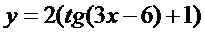
3.	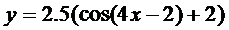4.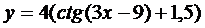
5.	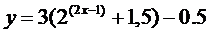6.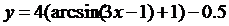
7.	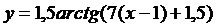8.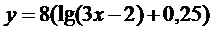
9.	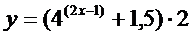10.
11.	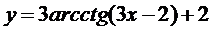12.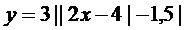
13.	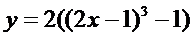14.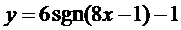
15.	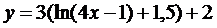16.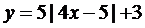
17.	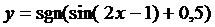18.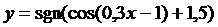
19.	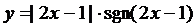20.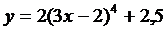
21.	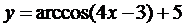22.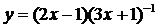
23.	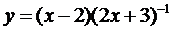24.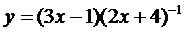
25.	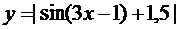26.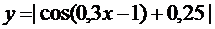
27.	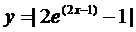28.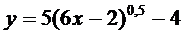
29.	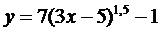30.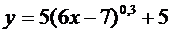