Понятие корреляционной связи

Тема 6: основы корреляционного анализа

Задачи корреляционного анализа

Корреляционный анализ состоит в определении степени тесноты корреляционной связи между переменными и количественной оценке тесноты этой связи. Корреляционный анализ следует применять только в том случае, если данные наблюдений или эксперимента можно считать случайными и выбранными из нормальной совокупности.

Перечислим задачи корреляционного анализа.

1. Установление направления корреляционной связи.

у у у

х х х

Положительная корреляция Отрицательная корреляция Нет корреляции

Рисунок 6.1

2. Установлениеформы связи (линейная, нелинейная).

3. Измерение тесноты связи с помощью ее количественной оценки – коэффициента корреляции.

4. Проверка значимости коэффициента корреляции, который выступает мерой связи между случайными величинами.

Укажем особенности корреляционной связи.

1)Корреляционная связь не может рассматриваться как свидетельство причинно-следственной зависимости. Она свидетельствует лишь о том, что изменения одного признака, как правило, сопровождаются определенными изменениями другого, то есть отражает согласованные изменения признаков, которые могут объясняться множеством причин, в том числе зависимостью обоих признаков от третьего признака или сочетания других признаков.

2)Корреляционная связь не дает ответа на вопрос, где находится причина изменений – в одном из признаков или за пределами исследуемой пары признаков.

Выборочный коэффициент линейной корреляции

Поставим вопрос: как оценить направление и силу линейной корреляционной связи с помощью коэффициента корреляции?

Для генеральной совокупности коэффициент корреляции, как правило, неизвестен, поэтому он оценивается по экспериментальным данным, представляющим собой выборку объема 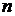пар значений 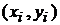, полученную при измерении двух признаков. Коэффициент корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции и обозначается символом .

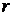Если связь между признаками имеет линейный характер, то коэффициент корреляции называется коэффициентом линейной корреляции Пирсона. Для оценки тесноты нелинейной связи служит корреляционное отношение.

Приведем формулу для вычисления выборочного коэффициента линейной корреляции:

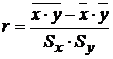. (6.1)

Тема 6: основы корреляционного анализа

Понятие корреляционной связи

Диалектический подход к изучению природы и общества требует рассмотрения явлений в их взаимосвязи и непрерывном изменении.

Одна из задач статистического исследования состоит в изучении связи, взаимозависимости между наблюдаемыми явлениями. Знание взаимозависимостей случайных величин дает возможность решить одну из кардинальных задач любого исследования: возможность предвидеть, прогнозировать развитие ситуации при изменении конкретных характеристик объекта исследования.

Различают два типа взаимосвязей между различными явлениями и их признаками: функциональнаязависимость и статистическаязависимость (либо независимость).

Если каждому определенному значению факторного признака 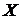соответствует по определенному закону вполне определенное значение результативного признака 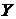, то такой вид причинной зависимости называется функциональной связью. В жизни функциональные связи встречаются далеко не всегда, поскольку каждая переменная определяется воздействием многих факторов – генетических, социальных, педагогических и т.д.

Вид причинной зависимости, проявляющийся не в каждом отдельном случае, а в общем, в среднем, при большом числе наблюдений, называется стохастической зависимостью.

Связи между психологическими переменными часто имеют не функциональный характер, а статистический. Статистической называется зависимость, при которой изменение одной случайной величины влечет изменение распределения другой случайной величины. Это означает, что каждому значению 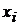независимой переменной 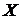соответствует не единственное значение другой переменной 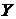, а некоторая совокупность значений 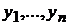. Переменная 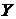ведет себя как случайная величина, поскольку имеет некоторую свободу, подвержена влиянию контролируемых и неконтролируемых факторов, измеряется с некоторой случайной ошибкой. Значения 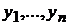можно упорядочить, например, по возрастанию 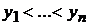и найти частоты встречаемости каждого значения. Получим таблицу условных значений 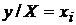(значение 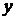при условии, что случайная величина 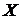приняла значение 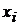) и соответствующих частот, которую называют условным распределением СВ .

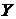Зависимость, при которой каждому значению одной случайной величины соответствует условное распределение другой случайной величины, называется статистической или вероятностной зависимостью.

Поскольку статистическая зависимость между 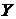и 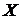неоднозначна, то представляет интерес «усредненная» закономерность в изменении условного математического ожидания .

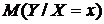Корреляционная связь –это зависимость среднего значения результативного признака от изменения факторного признака.

Функциональная зависимость между значениями одной переменной и условным математическим ожиданием другой переменной называется корреляционной зависимостью.

Использование термина «зависимость» подразумевает влияние признаков друг на друга, в отличие от термина «связь». Корреляционная связь – согласованное изменение двух признаков, отражающее факт, что изменчивость одного признака находится в соответствии с изменчивостью другого.

Корреляционная связь между признаками может возникать различными путями:

- важнейший путь - причинная зависимость результативного признака от вариации факторного признака;

- вместе с тем, корреляционная связь может возникнуть между следствиями общей причины;

- корреляция возникает и в случае, когда каждый из признаков - и причина, и следствие.