ТЕМА 5: Средние величины и показатели вариации
ТЕМА 5: Средние величины и показатели вариации
Средние величины
Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.
Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие – средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок. Второе условие – для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются, и проявляется общее свойство (типичный размер признака) для всей совокупности.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.
В экономических исследованиях и плановых расчетах применяются две категории средних:
- степенные средние;
- структурные средние.
К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая. Величины, для которых исчисляется средняя, обозначаются буквой хi. Средняя обозначается через 
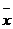. Такой способ обозначения указывает на происхождение средней из конкретных величин. Черта вверху символизирует процесс осреднения индивидуальных значений. Частота– повторяемость индивидуальных значений признака – обозначается буквой f.
Формулы средних величин могут быть получены на основе степенной средней, для которой определяющей является управление:
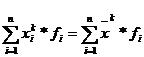, откуда 
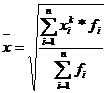. (5.1)
В дальнейшем при написании формул средних подстрочные значки i, n использоваться не будут, но подразумевается, что суммируются все произведения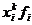 
.
В зависимости от степени k получаются различные виды средних величин, их формулы представлены в таблице 5.1.
Как видно из таблицы 5.1, взвешенные средние учитывают, что отдельные варианты значений признака имеют различную численность, поэтому каждый вариант «взвешивают» по своей частоте, т.е. умножают на нее. Частоты f при этом называются статистическими весами или просто весами средней. Однако необходимо учитывать, что статистический вес – понятие более широкое, чем частота. В качестве веса могут применяться какие-либо другие величины (в таблице 5.1 они обозначены буквой w). Например, при расчете средней продолжительности рабочего дня по предприятию единственно правильным будет взвешивание по количеству отработанных человеко-дней. Частоты отдельных вариантов могут быть выражены не только абсолютными величинами, но и относительными – частостями.
Вопрос о выборе средней решается в каждом отдельном случае, исходя из задачи исследования, материального содержания изучаемого явления и наличия исходной информации. Он состоит из нескольких этапов:
1) устанавливается определяющий показатель, т.е. обобщающий показатель совокупности, от которого зависит величина средней;
2) определяется математическое выражение для определяющего показателя;
3) производится замена индивидуальных значений средними величинами;
4) решение уравнения средней.
Основополагающее правило при этом заключается в том, что величины, представляющие собой числитель и знаменатель средней, должны иметь определенный логический смысл.
Таблица 5.1 - Формулы различных видов степенных средних величин
| Значение k | Наименование средней | Формула средней | |
| простая | взвешенная | ||
| -1 | Гармоническая |  |  ;  |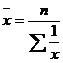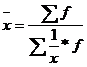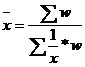
| Геометрическая |   |  | |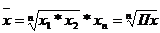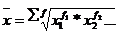
| Арифметическая |  |  ;  | |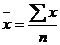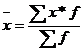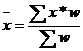
| Квадратическая |  |  |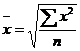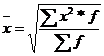
Структурные средние – мода и медиана – в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности.
Медианойназывается значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.
Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания значений признака.
Для определения медианы сначала определяют ее место в ряду, используя формулу 5.2:
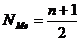, (5.2)
где n – число членов ряда.
Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую их двух срединных значений.
Модойназывается значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).
Кривые распределения
Наиболее надежный путь выявления закономерностей распределения – увеличение количества наблюдений. По мере увеличения количества наблюдений (в пределах той же однородной совокупности) при одновременном уменьшении величины интервала закономерность, характерная для данного распределения, будет выступать все более и более ясно, а представляющая полигон частот ломаная линия будет приближаться к некоторой плавной линии и в пределе должна превратиться в кривую линию.
Кривая линия, которая отражает закономерность изменения частот в чистом, исключающем влияние случайных факторов виде, называется кривой распределения.
В настоящее время изучено значительное число различных форм распределений. В практике статистических исследований часто используется распределение Пуассона, Максвелла, особенно нормальное распределение. Распределения, близкие к нормальному распределению, были обнаружены при изучении самых различных явлений, как в природе, так и в развитии общества.
В статической практике большой интерес представляет решение вопроса о том, в какой мере можно считать полученное в результате статистического наблюдения распределение признака в исследуемой совокупности, соответствующее нормальному распределению.
Для решения этого вопроса следует рассчитать теоретические частоты нормального распределения, т.е. те частоты, которые были бы, если бы данное распределение в точности следовало закону нормального распределения. Для расчета теоретических частот применяется следующая формула:
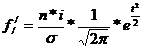, (5.36)
где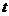 
- нормированное отклонение;
;
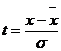величина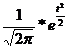 
- определяется по специальной таблице.
Следовательно, в зависимости от величины t для каждого интервала эмпирического ряда определяются теоретические частоты.
Для проверки близости теоретического и эмпирического распределений используются специальные показатели, называемые критериями согласия. Наиболее распространенным является критерий согласия К.Пирсона х2(«хи-квадрат»), исчисляемый по формуле: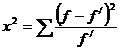 
, (5.37)
где f – эмпирические частоты (частости) в интервале;
f/ - теоретические частоты (частости) в интервале.
Полученное значение критерия (х2расч) сравнивается с табличным значением (х2табл). Последнее определяется по специальной таблице (см. приложение 2) в зависимости от принятой вероятности (Р) и числа степеней свободы k (для нормального распределения k равно числу групп в ряду распределения минус 3).
Если х2расч £ х2табл , то гипотеза о близости эмпирического распределения к нормальному не отвергается.
При расчете критерия Пирсона необходимо соблюдать условия: число наблюдений должно быть достаточно велико (n ³ 50); если теоретические частоты в некоторых интервалах меньше 5, то интервалы объединяют так, чтобы частоты были больше 5.
Используя величину х2 , В.И.Романовский предложил оценивать близость эмпирического распределения кривой нормального распределения по отношению:
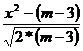, (5.38)
где m – число групп;
n – 3 - число степеней свободы при исчислении частот нормального распределения.
Если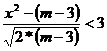 
, то можно принять гипотезу о нормальном характере эмпирического распределения.
Распространенным критерием согласия является критерий А.Н.Колмогорова:
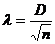, (5.39)
где D – максимальное значение разности между накопленными эмпирическими и теоретическими частотами;
n – сумма эмпирических частот.
По таблице значений вероятностей l-критерия находят соответствующую вероятность (Р). Если найденной величине l соответствует значительная по величине вероятность (Р), то расхождения между эмпирическим и теоретическим распределениями несущественны.
Практическое и научное значение имеет распределение Пуассона. Оно характерно для редко встречающихся явлений, поэтому его называют «законом редких явлений» (или «законом малых чисел»).
Закон Пуассона применяется для совокупностей, достаточно больших по объему
(n ³ 100) и имеющих достаточно малую долю единиц, обладающих данным признаком (р £ 0,1), например для распределения партий готовой продукции по числу забракованных изделий, печатных страниц по числу опечаток, станков по числу отказов, ткацких станков по числу обрывов нити и т.д.
Теоретические частоты распределения Пуассона определяются формулой:
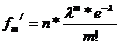, (5.40)
где n – общее число независимых испытаний;
l - среднее число появления редкого события в n одинаковых независимых испытаниях;
m - частота данного события (m = 0, 1, 2 …);
е – основание натуральных логарифмов, е = 2,71828.
Величина е-l определяется по специальной таблице; m! – произведение 1*2*3…*m ; 0! – считается равным единице.
Степень расхождения теоретических и эмпирических частот оценивается с помощью критериев согласия.
ТЕМА 5: Средние величины и показатели вариации
Средние величины
Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.
Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие – средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок. Второе условие – для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются, и проявляется общее свойство (типичный размер признака) для всей совокупности.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.
В экономических исследованиях и плановых расчетах применяются две категории средних:
- степенные средние;
- структурные средние.
К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая. Величины, для которых исчисляется средняя, обозначаются буквой хi. Средняя обозначается через 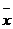. Такой способ обозначения указывает на происхождение средней из конкретных величин. Черта вверху символизирует процесс осреднения индивидуальных значений. Частота– повторяемость индивидуальных значений признака – обозначается буквой f.
Формулы средних величин могут быть получены на основе степенной средней, для которой определяющей является управление:
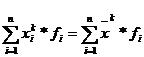, откуда 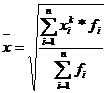. (5.1)
В дальнейшем при написании формул средних подстрочные значки i, n использоваться не будут, но подразумевается, что суммируются все произведения .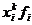
В зависимости от степени k получаются различные виды средних величин, их формулы представлены в таблице 5.1.
Как видно из таблицы 5.1, взвешенные средние учитывают, что отдельные варианты значений признака имеют различную численность, поэтому каждый вариант «взвешивают» по своей частоте, т.е. умножают на нее. Частоты f при этом называются статистическими весами или просто весами средней. Однако необходимо учитывать, что статистический вес – понятие более широкое, чем частота. В качестве веса могут применяться какие-либо другие величины (в таблице 5.1 они обозначены буквой w). Например, при расчете средней продолжительности рабочего дня по предприятию единственно правильным будет взвешивание по количеству отработанных человеко-дней. Частоты отдельных вариантов могут быть выражены не только абсолютными величинами, но и относительными – частостями.
Вопрос о выборе средней решается в каждом отдельном случае, исходя из задачи исследования, материального содержания изучаемого явления и наличия исходной информации. Он состоит из нескольких этапов:
1) устанавливается определяющий показатель, т.е. обобщающий показатель совокупности, от которого зависит величина средней;
2) определяется математическое выражение для определяющего показателя;
3) производится замена индивидуальных значений средними величинами;
4) решение уравнения средней.
Основополагающее правило при этом заключается в том, что величины, представляющие собой числитель и знаменатель средней, должны иметь определенный логический смысл.
Таблица 5.1 - Формулы различных видов степенных средних величин
| Значение k | Наименование средней | Формула средней | |
| простая | взвешенная | ||
| -1 | Гармоническая | | ; |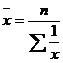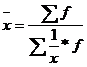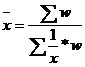
| Геометрическая | | | |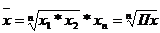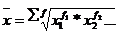
| Арифметическая | | ; | |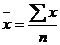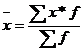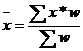
| Квадратическая | | |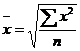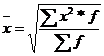
Структурные средние – мода и медиана – в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности.
Медианойназывается значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.
Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания значений признака.
Для определения медианы сначала определяют ее место в ряду, используя формулу 5.2:
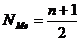, (5.2)
где n – число членов ряда.
Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую их двух срединных значений.
Модойназывается значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).