Составление уравнений состояния методом наложения

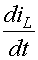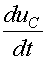При составлении уравнений состояния цепи заданными величинами являются переменные состояния i_L, u_С и источники ЭДС и токов, действующие в цепи, а производные и определяется величинами u_Lи i_С. Поэтому после коммутации цепь можно заменить эквивалентной, в которой каждый ток i_Lпредставлен источником тока, а каждое напряжение u_С – источником ЭДС. Например, цепи, представленной на рис. 2, соответствует эквивалентная цепь (рис. 6). Искомыми величинами при расчете этой цепи будут напряжение u_L и ток i₂.

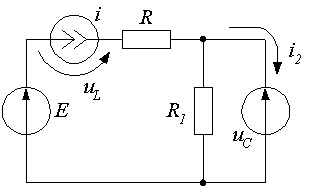
Рис. 6. Расчетная схема

Так как цепь состоит только из источников и активных сопротивлений, для расчета удобно применить метод наложения. Цепи (рис. 6) в этом случае будут соответствовать три частичные схемы, которые представлены на рис. 7,а, 7,б и 7, в.

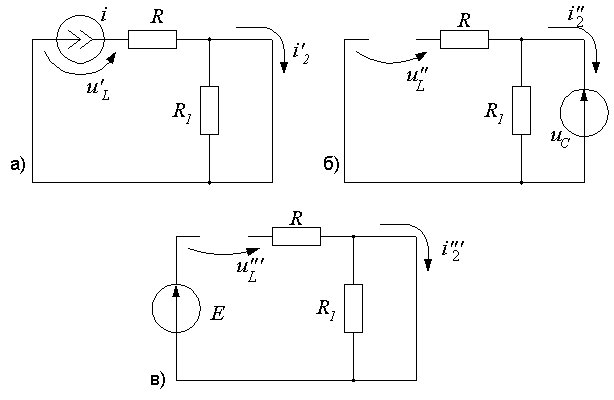
Рис. 7. Схемы частичных режимов

В связи с тем, что при применении метода наложения удаляемые источники ЭДС закорачиваются, а источники тока размыкаются, расчет полученных частичных схем не представляет большой сложности.

Для схемы рис. 7,а получаем: , ;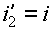

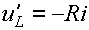для рис. 7,б: , ;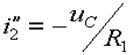

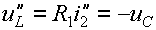для рис. 7,в: , .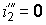

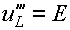Величины u_L и i₂ при совместном действии всех источников будут равны:

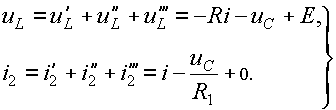(27)

Из сравнения уравнений (27) снайденными ранее (24) видим, что получены одинаковые результаты, поэтому дальнейшие действия совпадают с описаниями, приведенными в подразд. 4.2.

Решение уравнений состояния

Аналитическое решение уравнений состояния вида (21) для цепей, порядок которых больше двух, весьма громоздко, поэтому чаще всего они решаются численными методами на ЭВМ. В этом случае решение дифференциальных уравнений, составленных в форме Коши, сводится к их численному интегрированию. Разработаны различные методы численного интегрирования, которые позволяют рассчитывать значения искомых переменных через малые промежутки – шаги интегрирования h и получать решение в виде таблиц значений переменных для отдельных (дискретных) моментов времени. Любой метод численного интегрирования предполагает, что известны значения искомых переменных в начальный момент времени t=0 (начальные условия задачи). К наиболее простым методам численного интегрирования относятся явные методы, в которых искомые переменные определяются по уже найденным на предыдущем шаге значениям. К одношаговым методам относятся алгоритмы Рунге-Кутта различного порядка.

Важной проблемой численного интегрирования является выбор шага интегрирования h. Выбор излишне малого шага увеличивает время расчета и накопление ошибок округления. При слишком большом шаге может наблюдаться резкое увеличение погрешностей, т.е. с каждым последующим шагом численное решение все более отличается от истинного. В этом случае говорят о численной неустойчивости алгоритма. Все явные методы имеют ограничение величины шага интегрирования по условию обеспечения устойчивости. Оценить это значение можно, зная собственные значения основной матрицы 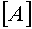уравнений состояния (21).

Собственные значения 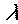матрицы 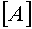находят, решая уравнение

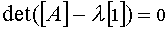, (28)

где 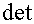– обозначение операции вычисления определителя; 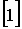– единичная матрица того же порядка, что и .

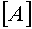Собственные значения матрицы 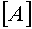совпадают с корнями характеристического уравнения цепи.

Наиболее просто определить величину шага интегрирования из условий обеспечения устойчивости для метода Рунге-Кутта первого порядка (метод Эйлера). При действительных собственных значениях матрицы 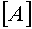необходимо выбирать шаг из условия 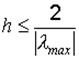, где 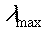– максимальное по абсолютной величине собственное значение матрицы 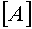. При наличии в собственных значениях комплексных величин вида 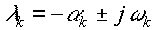шаг должен быть еще и меньше минимального из значений, вычисленных по формуле .

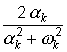Методы Рунге-Кутта более высоких порядков сохраняют численную устойчивость и при несколько больших величинах шага интегрирования. Поэтому, выбрав шаг и проверив его по описанным соотношениям, можно быть уверенным, что решение будет сохранять устойчивость при применении любого явного метода численного интегрирования.

Оценим по критерию устойчивости шаг интегрирования уравнений состояния для цепи, изображенной на рис. 2, при заданных ранее величинах.

Подставляя в уравнение (28) основную матрицу 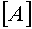из (26), записываем:

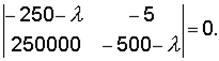
Раскрывая определитель, получаем (–250–l )(–500–l )+125 · 10⁴ = 0 или l ²+750l +1375000 = 0.

Решая полученное квадратное уравнение, находим собственные значения основной матрицы цепи l = –375± j1111.

Так как собственные значения представляют сопряженные комплексные величины, то шаг интегрирования должен удовлетворять условию

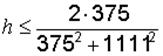
или h £5,45 · 10^–4с = 0,545 мс. Для удобства расчетов и снижения погрешности интегрирования принимаем шаг h = 0,1 мс.

На кафедре ТОЭ ДВГУПС разработана программа LIN (автор программы О.Г. Заволока), предназначенная для численного интегрирования уравнений состояния линейных электрических цепей с постоянными источниками. Перед выполнением расчетов с помощью данной программы необходимо подготовить следующие исходные данные:

• основную матрицу ;
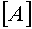• матрицу источников ;
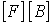• начальные значения переменных состояния i_L(0) и u_С(0);
• шаг интегрирования ;
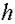• шаг вывода и время интегрирования.

Две последние величины определяют, с каким интервалом будут выводиться на печать результаты вычислений и момент окончания расчетов. Например, если рассчитываем периодический процесс и хотим вывести на печать результаты интегрирования в 10 точках в течение одного периода синусоидальной составляющей, то шаг вывода и время окончания расчетов определяем следующим образом:

• период колебания ;
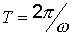• время окончания ;
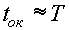• шаг вывода .

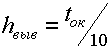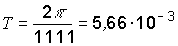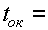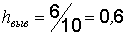Для рассматриваемого примера (w = 1111 рад/с) получаем с = 5,66 мс, принимаем 6 мс, мс.

Следует отметить, что шаг вывода не должен быть меньше шага интегрирования.

Ввод данных при работе с программой LIN осуществляется в диалоговом режиме и при наличии подготовленных исходных данных не вызывает затруднений. Значения шагов интегрирования и вывода, времени окончания расчетов должны быть выражены в миллисекундах. Результаты расчетов в виде таблицы выводятся на экран и могут быть распечатаны.

В качестве образца (табл.1) приведены выводимые на печать результаты расчета контрольного примера, рассматриваемого в работе. Они включают исходные данные, вводимые пользователем. Переменные состояния в таблице результатов расчета обозначены символом Х с индексами 1 и 2. Так как при составлении уравнений состояния в качестве первой переменной состояния применяется ток i, а второй – напряжение u_C, то Х[1] соответствует i, Х[2] – u_C.

Таблица 1

Результаты расчетов

Основная матрица А -250.000000 -5.000000000 250000.000 -500.000000
Вектор источников 5500.00000 0.0
Начальные условия 1.00000000 1050.00000
Шаг интегрирования – ввод: 0.100 мс; расчет: 0.100 мс Шаг вывода – ввод: 0.600 мс; расчет: 0.600 мс Время окончания – ввод: 6.000 мс; расчет: 6.000 мс
Т, мс 0.000 0.600 1.200 1.800 2.400 3.000 3.600 4.200 4.800 5.400 6.000	Х[1] 1.00000000 1.205777 1.640769 2.055534 2.298759 2.339575 2.235716 2.079334 1.949275 1.885748 1.888941	Х[2] 1050.00000 917.4994 864.5686 882.6195 939.0260 998.3144 1036.7631 1047.2177 1035.8235 1014.8562 995.8044