Бесконечный пучок и его практические приложения

Бесконечный пучок – пучок, в котором количество линий не ограничено.

1.Сост(ояния) CO: 1,2, ….k,

Входящий поток – простейший, Время обслуживания –

– марковский, ПГР,

, . – стац. реш-ие для беск. пучка.

Следствия: 1. Стац. решение распределено по закону Пуассона с параметром .
2 - показатель эффективности.

Замечание: Стационарное решение справедливо для распределения длины разговора.

2. Приложения:

1. Доставка телеграмм. СО – телеграф, линия – почтальон, доставляющий телеграмму, пучок линий – совокупность почтальонов, обслуживание - доставка. Поток телеграмм - простейший с параметром 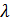за t поступает ровно k телеграмм с вероятностью , ( .

Допущения: 1)Каждый почтальон доставляет одновременно только одну телеграмму.

2) Каждая телеграмма начинает доставляться немедленно по ее получении телеграфом. – время доставки телеграммы и возврата почтальона – случайная величина ( - среднее время доставки.) Вероятность того, что в пути находится одновременно k почтальонов, .

2. Ремонт автомашин. СО – совокупность ремонтных мастерских. Вызов – автомашина, требующая ремонта. Обслуживание – ремонт. Пусть ремонт начинается немедленно по выходу машины из строя. Поток поломок – простейший с параметром .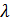
; - среднее время ремонта автомашины.

Упорядоченный пучок линий

Пример: упаковочный цех: конвейер с упаковочными автоматами. Вызов – готовое изделие, линии – упаковочные автоматы, обслуживание – упаковка.

Допущения:

-Входящий поток – простейший с параметром .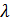

-Время обслуживания показательно распределено с параметром β.

Рассмотрим частичный пучок длины k (из первых k линий).

i-ая линия -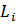

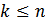(пучок конечный)или 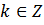(пучок бесконечен)

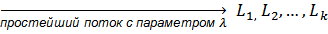
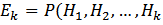) – вероятность отказа на пучке длины k .

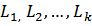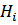- событие, состоящее в том, что на i-ой линии не осуществилось обслуживание.

-Вычисление 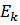– вероятность застать все линии занятыми.

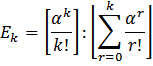
-Интепретация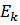

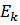- средняя доля времени, в течение которого заняты все k линий.

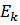- средняя доля вызовов, получающих отказ.

-Свойство 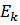(k=1,2…). Монотонно убывает.

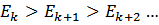
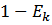- вероятность того, что вызов будет обслужен на какой-либо из первых k линий. (возрастает).

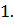Найдем закон распределения номера линии, на которой осуществляется обслуживание вызова. Обслуживание на k-ой линии: ξ: 1, 2, …, k, …

Найти 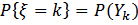. (вероятность успеха в k-ом испытании).

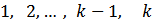
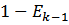
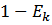
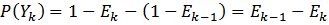>0 (по свойству 1)

Пусть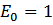

ξ = 1 2 … k

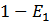
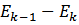
2. С ростом номера линии интенсивность потока падает.

Пусть 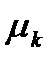- интенсивность стационарного потока, пущенного на k-ую линию.

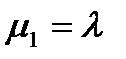- интенсивность входящего потока.

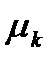для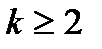

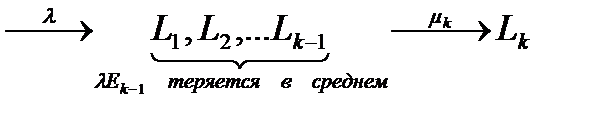
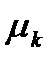- среднее число вызовов в единицу времени.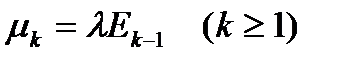

	Вероятности исходов	интенсивности
Отказ на частичном пучке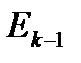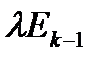
обслуживание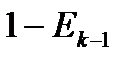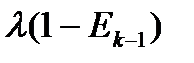

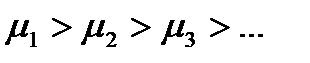
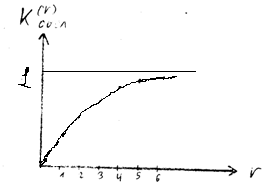
3. Поток все полнее обслуживается с повышением номера линии (полнота обслуживания измеряется коэффициентом обслуживания , ).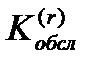

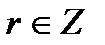а) 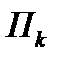- вероятность отказа на линии r при условии того, что вызов поступил на эту линию.

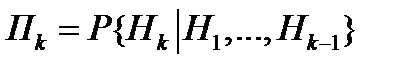
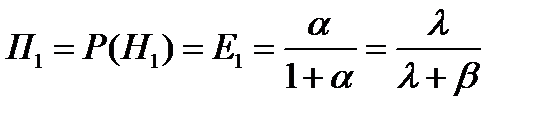
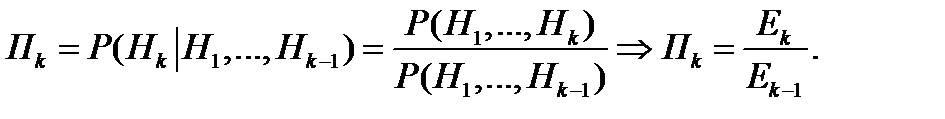
б) 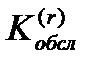- коэффициент обслуживания – это среднее число обслуженных вызовов за единицу времени.

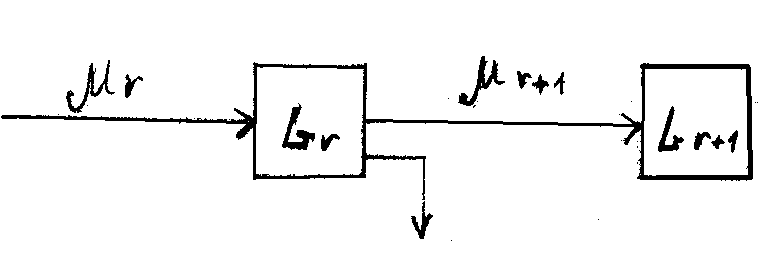
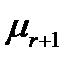- отказы, 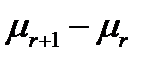- обслуживаются.

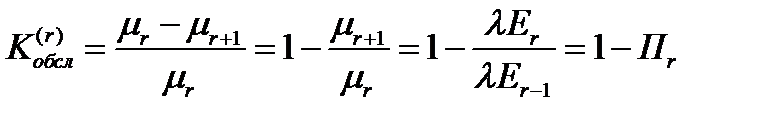
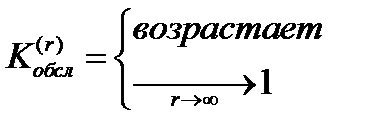
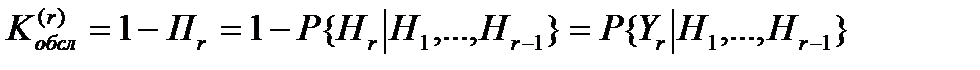- вероятность того, что вызов будет обслужен на r-ой линии при условии того, что вызов поступил на r-ую линию.

16.Упорядоченный пучок групп линий

Организация обслуживания.

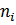– число линий в группе с номером i.

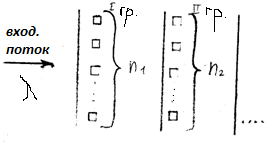
Входящий поток – простейший с параметром 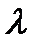. Время обслуживания распределено показательно с параметром 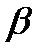. Поступающий вызов сначала направляется в группу I если все линии заняты переходит в группу II, до тех пор пока не попадет в группу в которой есть свободные места. I, II, …, k – част. пучок длины k.(где I, II – группы)

Пусть 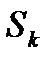- суммарное число линий в первых k группах.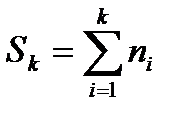

Вероятность отказа на част. пучке длины k:

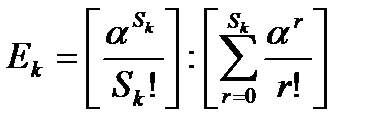, где k – количество групп.

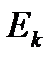- вероятность пройти без обслуживания первых k групп. 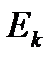– монотонно убыв. числовая посл.

Постановка экстремальной задачи

.

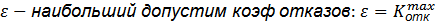Пример упорядоченных пучков групп линий.

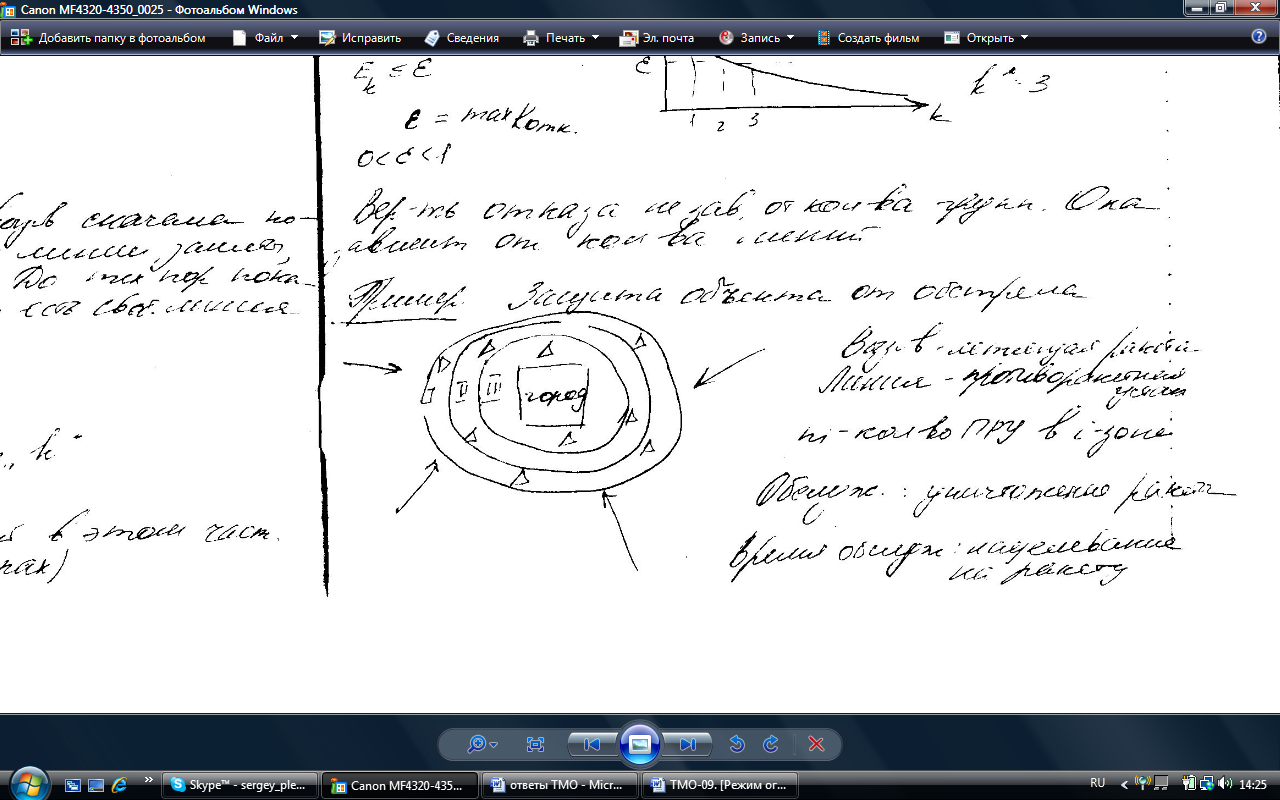1).Защита объектов. Вызов – летящая ракета. Линия – ПРУ, Простейший поток ракет. Пусть 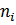– количество ПРУ в i-ой зоне. Обслуживание – уничтожение ракеты, время обслуживания – время нацеливания на ракету.

E_k – ракета не будет сбита в первых k зонах.

E₁ =0,2; E₂ =0,015 ; E₃ =0,003: 200 из 1000 ракет преод. зону I, 15 – зону II, 3 – зону III.