Основные закономерности построения навигационных комплексов
Принцип действия навигационного комплекса основан на моделировании движения летательного аппарата относительно навигационных систем отсчета под действием совокупности сил тяги, сопротивления атмосферы и тяготения Земли. Это означает, что состав датчиков первичной информации, системы взаимосвязей, вычислительных устройств и вся структура комплекса должны воспроизводить законы динамики ЛА как твердого тела, а также кинематики движений относительно ориентиров, расположенных на земной поверхности, в воздушной среде и космическом пространстве.
Комплексная обработка информации, осуществляемая в навигационном комплексе, позволяет получить на выходе системы искомые параметры вектора навигационного состояния ЛА с необходимыми точностью и надежностью.
Чтобы оценить состав параметров этого вектора, рассмотрим уравнения движения ЛА как твердого тела с массой 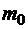 относительно геоцентрической системы координат
относительно геоцентрической системы координат 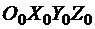 (рис. 3):
(рис. 3):
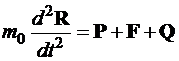 ; (1)
; (1)
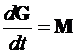 , (2)
, (2)
где  ,
,  ,
, 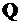 – векторы сил тяги, сопротивления среды и тяготения Земли соответственно;
– векторы сил тяги, сопротивления среды и тяготения Земли соответственно;  – радиус-вектор центра масс летательного аппарата;
– радиус-вектор центра масс летательного аппарата; 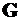 – кинетический момент тела летательного аппарата относительно не вращающейся системы координат с началом в центре масс летательного аппарата;
– кинетический момент тела летательного аппарата относительно не вращающейся системы координат с началом в центре масс летательного аппарата; 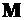 – вектор вращающего момента, приложенного к ЛА.
– вектор вращающего момента, приложенного к ЛА.
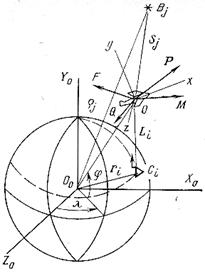
Рис. 3. Схема движения летательного аппарата под действием сил и моментов относительно навигационной системы отчета и ориентиров
Если учесть, что навигационная система отсчета может вращаться с угловой скоростью 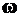 , корпус летательного аппарата – с угловой скоростью
, корпус летательного аппарата – с угловой скоростью 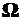 относительно инерциального пространства, то из уравнений динамики (1) и (2) найдем связи между параметрами вектора навигационного состояния, включая:
относительно инерциального пространства, то из уравнений динамики (1) и (2) найдем связи между параметрами вектора навигационного состояния, включая:
вектор ускорения относительно вращающейся навигационной системы координат
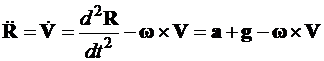 ; (3)
; (3)
вектор скорости движения
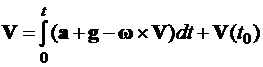 ; (4)
; (4)
вектор положения
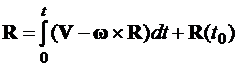 ; (5)
; (5)
вектор угловой скорости корпуса, определяемый из уравнения
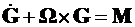 , (6)
, (6)
где 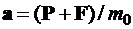 ;
; 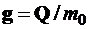 – векторы ускорения от активных сил и сил тяготения соответственно;
– векторы ускорения от активных сил и сил тяготения соответственно; 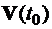 ,
, 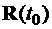 – начальные значения векторов
– начальные значения векторов 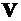 и
и  (в момент времени
(в момент времени 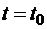 ).
).
Взаимосвязь между системами координат 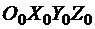 и
и 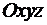 определяется с помощью матрицы направляющих косинусов, зависящих от трех углов поворота систем координат относительно друг друга.
определяется с помощью матрицы направляющих косинусов, зависящих от трех углов поворота систем координат относительно друг друга.
Следовательно, динамическая часть вектора навигационного состояния содержит по три составляющих векторов ускорения, скорости и местонахождения относительно навигационной системы отсчета, три составляющих угловой скорости летательного аппарата и три угла его поворота относительно навигационной системы координат (всего 15 параметров состояния), связанных между собой уравнениями (3)…(6).
Кинематическая часть навигационного вектора состояния содержит параметры положения и движения летательного аппарата относительно навигационных ориентиров.
Относительное положение летательного аппарата и ориентиров (см. рис. 2) определяется из уравнений:
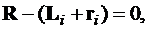
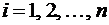 ; (7)
; (7)
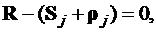
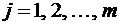 , (8)
, (8)
где 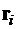 и
и 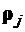 – радиус-векторы местонахождения ориентиров
– радиус-векторы местонахождения ориентиров 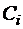 ; и
; и 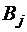 относительно навигационной системы отсчета;
относительно навигационной системы отсчета; 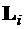 ; и
; и 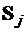 – радиус-векторы ориентиров относительно летательного аппарата.
– радиус-векторы ориентиров относительно летательного аппарата.
Скорости летательного аппарата относительно ориентиров находятся из уравнений (7), (8):
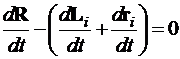 ; (9)
; (9)
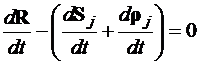 . (10)
. (10)
Уравнения (3)…(10) могут использоваться для определения скорости полета, а также координат местонахождения ЛА и ориентиров.
