Построение нормального эвольвентного зубчатого зацепления

Построение целесообразно выполнять на отдельном листе плотной бумаги.

Для точности построения рекомендуется принимать масштабную высоту зуба не менее 30 мм, ориентируясь на стандартные ряды масштабов:

- натуральная величина - 1:1;

- масштабы уменьшения -1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000;

- масштабы увеличения - 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1.

Для построения зубчатого зацепления переводим все полученные ранее действительные размеры в чертежные.

Проводим линию центров (рис.16), отмечаем на ней центры О₁ и О₂ на расстоянии a_w’ (центры колес О₁ и О₂ могут выходить за пределы чертежа).

В выбранном нами масштабе вычерчиваем окружности зубчатых колес: основные, начальные, делительные, окружности высту­пов и впадин.

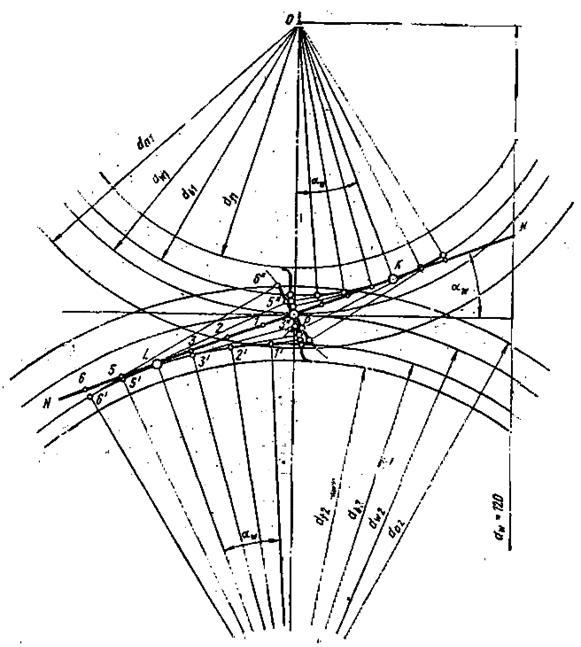
Рис.16 Схема построения эвольвентных профилей зубчатых колес

Через полюс зацепления Р (получается при касании начальных окружностей) проводим общую касатель­ную к начальным окружностям перпендикулярно к линии центров) и линию зацепления NN, касательную к основным окружностям, проведенную к радиусам, расположенным под углом α_w.

Строим эвольвентные профили зубьев для каждого колеса. Эвольвентной окружности называется кривая, описывае­мая точкой прямой линии, перекатываемой по этой окружно­сти без скольжения (рис.17). Окружность, по которой перекатывается прямая при образовании эвольвенту, называется основной окружностью. Следовательно, эвольвентные участки зубьев будут находиться в пределах между основными окружностя­ми и окружностями выступов колес.

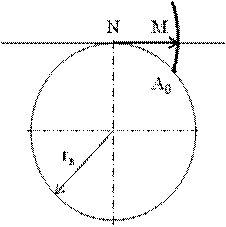
Рис.17 Схема, поясняющая физический смысл эвольвенты

Нетрудно убедиться, что отрезок NM является переменным радиусом кривизны эвольвенты при перекатывании прямой по основной окружности. Этот отрезок всегда касается окружности в точке N, а его величина равна длине дуги А₀N (NM = È А₀N).

Эти свойства эвольвенты позволяют с достаточной для практических целей точностью построить эвольвентный профиль зуба. Для этого относительно произвольно выбранной точки А₀ на основной окружности (рис.18) обозначим несколько точек 1, 2, 3, 4, 5 с таким расчетом, чтобы отрезки (хорды) А₀1 = 1-2 = 2-3 = 3-4 = 4-5 незначительно отличались от дуги ÈА₀1 = È1-2 = È2-3 = È3-4 = È4-5.

Линия зацепления NN касается основных окружностей в точках K и L и проходит через полюс зацепления (проверка правильности построения). Участок KL называется теоретическим участком линии зацепления.

Каждый зуб зубчатого колеса находится в зацеплении не на всем своем пути, а только на каком-то участке, т. е. в какой-то точке он входит в зацепление, а в какой-то выходит из него. Этот участок, лежащий на линии зацепления NN и образованный пересечением этой линии с. окружностями выступов_; называется практическим или рабочим участком ли­нии зацепления. На рис.17 практический участок линии, за­цепления обозначен точками А и В.

только центральной па­ры сопряженных зубьев так, чтобы они касались в полюсе за­цепления Р (рис.15).

Построение эвольвенты производим общепринятым мето­дом. Для этого отрезок LP линии зацепления (второго коле­са) разбиваем на равное число частей (допустим, на четыре), обозначим точки деления 1, 2, 3, 4 и т. д., продолжив деление по другую сторону точки L.

Отрезок LP линии зацепления играет роль производящей прямой, при обкатывании которой без скольжения по основ­ной окружности точка Р опишет эвольвенту.

Полученные отрезки Р—1,1—2, 2—3 . . ., начиная от точ­ки L, отложим по хорде на основной окружности, при этом разностью между длинами дуги и хорды пренебрегаем. Полу­ченные точки обозначим 1¹, 2', 3' . . .

Соединим эти точки с центром колеса и проведем через них касательные к основной окружности, которые будут пер­пендикулярны радиусам.

Отложим на касательных отрезки, равные расстоянию до полюса Р от соответствующей точки деления, т. е. вдоль пер­вой касательной откладываем отрезок Р—1, вдоль второй касательной — отрезок Р—2 и т.д. Полученные точки обозна­чим 1", 2", 3"...................... и. затем последовательно соединим их плавной кривой. Данная кривая и будет представлять эвольвентный участок профиля зуба. Для сопряженного колеса эвольвентный профиль зуба строится аналогично.

Неэвольвентный участок профилей зубьев, т. е. участок в пределах от основной окружности до окружности впадин, для случая d_f<d_b очерчивается радиальными прямыми, после чего у основания зуба производят их сопряжение с окружно­стями впадин радиусом (0,2÷0,3)m.

Если d_f>d_b, то сначала получают точку пересечения ок­ружности впадин с эвольвентой, а затем у основания дела­ют закругления радиусом (0,2÷0,3)m.

Для построения симметричного профиля зуба по окружности вершин зубьев откладываем половину ширины зуба S_a’/2 и проводим ось симметрии зуба. Затем методом зеркальной симмет­рии и шаблонов строим профиль зуба (рис. 16).

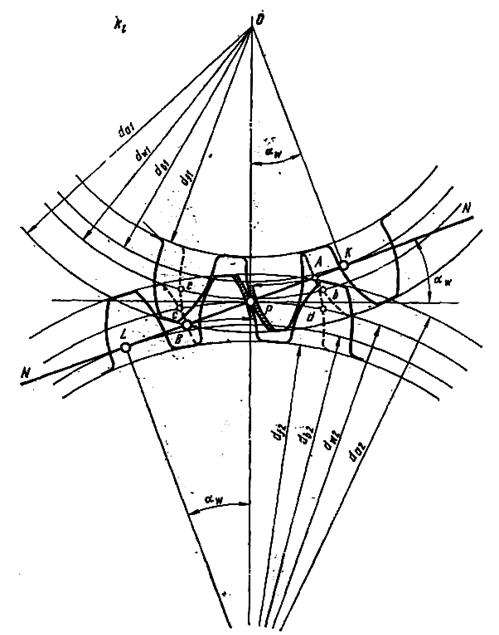
Рис.16 Зацепление зубчатых колес с обозначением рабочих участков профилей зубьев

Вырезаем готовые зубья и, прикладывая их эвольвентные профили к полюсу зацепления, обводим по одному зубу для каждого колеса. Для построения еще по одному зубу справа и слева от полученных определяем углы отклонения осей соседних зубьев от осей построенных:

α_z1 = 360⁰/z₁; α_z2 = 360⁰/z₂

Проводим оси соседних зубьев и обводим их профили по полученным ранее шаблонам.

Обозначим рабочие участки профилей зубьев. Учитывая, что в точке А начинается зацепление, т. е. в ней контактируются крайняя точка головки зуба второго (большого) коле­са и наинизшая точка ножки зуба первого (малого) колеса, радиусом О₁А сделаем засечку на профиле зуба малого коле­са, которая определит нам положение наинизшей точки первого колеса. Делая засечку на профиле зуба второго (боль­шего) колеса радиусом О₂В, определим наинизшую точку, участвующую в зацеплении, для этого колеса. Рабочие участ­ки профилей зубьев на чертеже отмечены штриховкой.

Определим длину дуги зацепления по любой из окружно­стей, в пределах которой происходит зацепление зубьев, пред­варительно проведя пунктиром через точки А и В сопряжен­ные профили в положении начала и конца зацепления. Дуги cd и ef между положениями, соответствующих профилей зубь­ев в начале и конце зацепления для каждого из колес есть пу­ти, проходимые зубьями за время зацепления одной пары зубьев, измеренные по начальной окружности. Эти дуги и на­зываются дугами зацепления.

На одном из зубчатых колес вычерчивается станочное зацепление зубчатой рейки и нарезаемого колеса с указанием размеров рейки и величины смещения (рис.17).

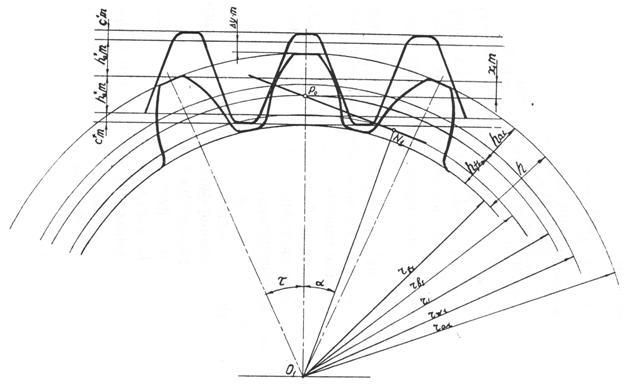
Рис.17 Схема расположения реечного инструмента

Литература

1. Теория механизмов и механика машин. Под ред Фролова К.В.

м.Наука 2004.

2. С.А. Попов, Г.А.Тимофеев Курсовое проектирование по теории механизмов и машин. м.1999.

3. Щепетильников В.А., Солодилов В.Я.. Геометрический синтез зубчатых колес внешнего зацепления со смещением. м.2001.