Нормированное и нормальное уравнения прямой

Вектору 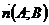соответствует единичный вектор – орт = 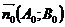, где , . Для того чтобы найти его координаты, достаточно нормировать его, т.е. разделить координаты вектора 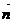на его модуль (длину).

Разделим коэффициенты общего уравнения Ах+Ву+С=0 на длину вектора .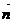

Так как , то получим уравнение или А₀х+В₀у+С₀=0. Это нормированное уравнение прямой.

Определение 4.

Нормированным уравнением прямой называется общее уравнение А₀х+В₀у+С₀=0, для которого 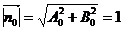. Множитель 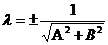называется нормирующим множителем.

Определение 5.

Нормированное уравнение прямой называется нормальным, если свободный член в нем отрицателен.

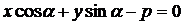(12.17)

Так как геометрический смысл координат орта вектора: 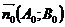= = 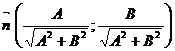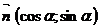, то для того чтобы получить из общего уравнения прямой нормальное уравнение, нужно разделить длину вектора нормали, взятую со знаком, противоположным знаку свободного члена.

Пример 2. Составим нормальное уравнения прямой АВ, если А(1;–2), В(0;5).

Решение. 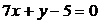– общее уравнение прямой АВ (см. пример 1):

Из уравнения вектор 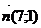, тогда 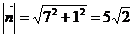, разделим все члены уравнения на длину вектора нормали: 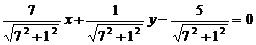, откуда получим – нормированное уравнение.

Т.к. свободный член отрицателен, то это и нормальное уравнение прямой АВ.

Пример 3. Составим уравнения медианы АМ и высоты АН Dтреугольника АВС, если А(1;–2), В(0;5), С(–1;3).

Решение.

1) Так как М – середина ВС, то координаты точки М (–0,5; 4).

Составим уравнение АМ: 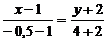, т.е. .

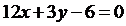2) Составим уравнение АН, проходящей через точку А перпендикулярно вектору 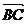(–1;–2): 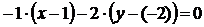или .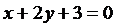

Аффинные и метрические задачи по теме «Прямая»

Взаимное расположение двух прямых

Пусть даны прямые и .

Исследуем их расположение. Для этого исследуем систему уравнений (2´2) на совместность и определенность:

. Составим расширенную матрицу системы .

Возможны случаи:

Условие	Характеристика системы	Взаимное расположение прямых
	Совместна и определена	Прямые пересекаются
, т.к. n=2	Совместна и не определена	Прямые совпадают
	Несовместна	Прямые параллельны (различны)

Условие параллельности прямых, заданных общими уравнениями:

(в широком смысле) (12.18).

В частности, условие совпадения прямых:

. (12.19).

Условие параллельности прямых, заданных уравнениямиy=k₁x+b₁ и y=k₂x+b₂:

k₁=k₂. (12.20).

Расстояние от точки до прямой

Пусть дана точка М₀(х₀;у₀) и прямая 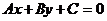, где

Расстояние от точки М₀(х₀;у₀) до прямой :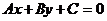

(12.21)

Расстояние от начала координат О (0; 0) до прямой :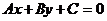

(12.22)

где р взято из нормального уравнения прямой .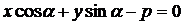

Угол между прямыми

Пусть даны прямые 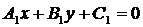и .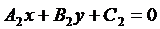

Угол между прямыми: 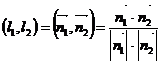, тогда

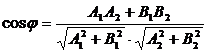(12.23)

Условие перпендикулярности прямых, заданных общими уравнениями:

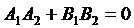(12.24)

Условие параллельности прямых, заданных уравнениямиy=k₁x+b₁ и y=k₂x+b₂:

k₁×k₂=–1 (12.25)

Пример 4. Вычислим угол А треугольника АВС, если А(1;–2), В(0;5), С(–1;3).

Решение.

Угол А – это угол между прямыми АВ и АС. Составим общие уравнения прямых:

прямая АВ: 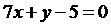; прямая АС: .

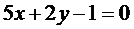Вычислим угол А: 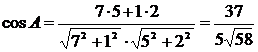»0,9717, ÐА»14^о.

Пример 5. Вычислим длину высоты АН DАВС, если А(1;–2), В(0;5), С(–1;3).

Решение. Длина высоты АН – расстояние от точки А до стороны ВС.

Составим уравнение ВС: , .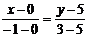

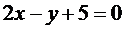Вычислим расстояние: .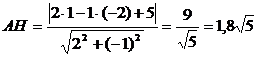

4.3. Геометрический смысл знака трехчлена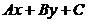

Множество всех точек М, координаты которых обращают трехчлен 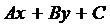в нуль, есть прямая, заданная общим уравнением, т.е.

l: 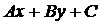=0.

Прямая делит плоскость на две полуплоскости и 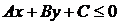(с границей). Геометрический смысл знака трехчлена 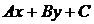состоит в том, что для всех точек одной полуплоскости, границей которой является прямая l: 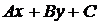=0, этот знак один и тот же. Для того, чтобы установить, лежат ли точки по одну и ту же сторону от прямой или же по разные стороны от нее, достаточно подставить их координаты в трехчлен и сравнить знаки полученных результатов.

Домашнее задание. Заполнить таблицу по образцу:

Условие	Уравнение	Название уравнения
Аффинная система координат
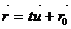		векторное
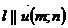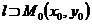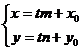,		параметрические
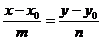		каноническое
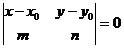		в форме определителя
		общее
		в отрезках
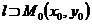		прямой, проходящей через две точки
Прямоугольная система координат
		прямой, проходящей данную точку перпендикулярно данному вектору
		с угловым коэффициентом
		нормированное
		нормальное