Тройные интегралы, их свойства

Пусть функция f(x,y,z) определена в ограниченной замкнутой пространственной области T. Разобьем T произвольным образом на n элементарных областей T₁,T₂,…,T_n с диаметрами d₁, d₂,…,d_n и объемами ∆V1, ∆V2,… ∆Vn В каждой элементарной области возьмем произвольную точку P_k(x_k, y_k, z_k) и умножим значение функции в точке P_k на объем этой области: .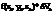

Выражение 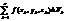называется интегральной суммой для функции f(x;y;z) по области T.

Предел интегральной суммы при стремлении к нулю наибольшего из диаметров элементарных областей называется тройным интеграломот функции f(x;y;z) по области T и обозначается:

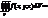
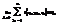
Основные свойства тройных интегралов аналогичны свойствам двойных интегралов. Если f(x;y;z) есть функция распределения плотности вещества в области T, то тройной интеграл численно равен массе всего вещества в этой области (физический смысл тройного интеграла).

Вычисление двойных и тройных интегралов в прямоугольных координатах.

Вычисление двойных интегралов в прямоугольных координатах

Если функция f(x;y) непрерывна в правильной области D, то двойной интеграл равен двукратному интегралу от этой же функции в области D: .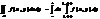

Сначала вычисляется внутренний интеграл, в котором x считается постоянным.

Вычисление тройных интегралов в прямоугольных координатах

Если функция f(x;y) непрерывна в некотором правильном теле V, то тройной интеграл равен трехкратному интегралу по тому же телу и вычисляется по формуле:

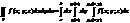
Билет. Основные понятия (определение, порядок, общее и частное решение и интеграл, задача Коши, теорема существования и единственности).

Дифференциальным уравнениемназывается уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы). Если независимая переменная одна, то уравнение называется обыкновенным, если же переменных две или больше, то уравнение называется дифференц. уравнением в частных производных. Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Решением дифференц. уравнения называется такая функция y=φ(x), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество. Процесс нахождения решения дифференц. уравнения называется интегрированием уравнения. Общим решением уравнения y’=f(x,y) называется функция y= φ(x,С). Всякое решение y= φ(x,С₀), получающееся из общего при конкретном значении C=C₀ ,называется частным решением. Если зависимость x от y находится в неразрешенном относительно y виде, то его называют общим интегралом.

F(x,y,y’)=0 – общий вид дифференциального уравнения первого порядка или в разрешенном относительно y’ виде: y’=f(x,y) (1). Пусть требуется найти функцию y(x), являющуюся решением уравнения (1) и удовлетворяющую условию: y(x₀)=y₀ (2). Такая задача называется задачей Коши или начальной задачей, а условие (2) называется начальным условием.Теорема существования и единственности решения( Теорема Пикара, Пеано, Коши): Если функция f(x;y) непрерывна в ограниченной области D, содержащей M₀(x₀;y₀) – начальную точку, т.е. |f(x;y)|≤M, M>0 и если частная производная по y в той же области D ограниченна, т.е. | 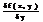|≤K, K>0, то существует единственное решение дифференц. уравнения (1), удовлетворяющее условию (2). Это решение будет непрерывно дифференцируемым в окрестности начальной точки. Геометрически это означает, что проходит единственная кривая через точку M₀(x₀;y₀), уравнение которой удовлетворяет дифференциальному уравнению.