Интегрирование некоторых иррациональных ф-ий

2.

Теорема (необходимое и достаточное условие постоянства функции):

Пусть у=f(х) определена и непрерывна на множестве Х и внутри этого множества имеет конечную производную f’(x), на границе множества сохраняет непрерывность, если принадлежит Х.

Для того, чтобы f(x) была const на множестве Х, необходимо, чтобы f’(x)=0 внутри множества Х.

Достаточные условия возрастания и убывания функции:

Для того, чтобы f(x) была возрастающей (убывающей), достаточно чтобы f’(x)>0 (f’(x)<0) для всех х, принадлежащих множеству Х.

3.

1ое достаточное условие экстремума функции:

Пусть х₀ – критическая точка 1ого рода. Предположим, что у=f(x) дифференцируема в некоторой окрестности (х₀-δ,х₀+δ) и f’(x) сохраняет свой знак слева и справа от х₀.

Значит: если при переходе через х₀ f’(x) меняет знак с + на -, то в т. х₀ f(x) имеет максимум, если с – на +, то минимум, если знак не меняется, то х₀ не является экстремумом.

2ое достаточное условие экстремума функции:

Пусть х₀ – стационарная точкам, в которой f(x) дважды дифференцируема, тогда если f”(х)<0, то х₀ – максимум, f”(х)>0, то х₀ – минимум (если равно 0, то не работает).

4.______

Пусть у=f(x) дифференцируема на (а,в), графиком ее является некоторая кривая.

Выпуклость кривой:Кривая у=f(x) называется выпуклой на (а,в), если все точки кривой лежат ниже любой ее касательной на этом интервале.

Вогнутость кривой:Кривая у=f(x) называется вогнутой на (а,в), если все точки кривой лежат выше любой ее касательной на этом интервале.

Точки перегиба:Точки, в которых выпуклость сменяется на вогнутость и наоборот, называются точками перегиба.

Теорема (достаточное условие выпуклости/вогнутости):

Пусть у=f(x) дважды дифференцируема на промежутке (а,в), тогда:

Если на (а,в) f”(x)>0, то кривая вогнутая;

Если на (а,в) f”(x)<0, то кривая выпуклая.

Теорема (достаточное условие перегиба):

Пусть х₀ – критическая точка 2ого рода, тогда:

Если при переходе через т. х₀ f” меняет знак с + на -, то х₀ – т. перегиб

Если с – на +, то выпуклость на вогнутость.

7.Понятие функции нескольких переменных:

Рассмотрим множество D, состоящее из пар действительных чисел (х,у). Любую пару чисел можно изобразить на плоскости точкой.

Если каждой паре действительных чисел соответствует одно определенное число z?Z, то говорят, что на множестве D задана функция z=f(x,y) со значениями во множестве Z.

Функцию z=f(x,y) называют функцией двух переменных, а переменные х и у – независимыми переменными.

Определение предела и непрерывности функции двух переменных:

Пусть функция f(x,y) определена внутри некоторой окрестности точки (х₀,у₀) кроме, может быть, самой точки.

Число А называется пределом функции z=f(x,y) в точке М₀ (х₀,у₀), если для любой последовательности точек {(x_n,y_n)} области определения функции, отличных от (х₀,у₀) и сходящихся к (х₀,у₀), последовательность значений функции {(x_n,y_n)} сходится к А:

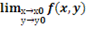=A.

Если 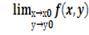=f(х₀,у₀), то функция f(x,y) называется непрерывной в точке (х₀,у₀).

8.Частные производные функции нескольких переменных:

Если существует предел

,

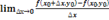
то он называется частной производной функции zпо х в точке 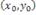и обозначается символами или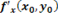

.

Аналогично определяется частная производная по у: = =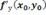

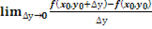
Полный дифференциал функции нескольких переменных:

Полным дифференциалом функции z=f(x,y) называется выражение вида dz = 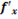(x,y)dx + 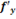(x,y)dy, где dx=∆х, dy=∆у.

Является суммой частных дифференциалов.

9.Экстремум функции нескольких переменных:

Функция z=f(x,y) имеет в точке М₀ (х₀,у₀) максимум (минимум) f(х₀,у₀), если вблизи этой точки для всех точек М, отличных от М₀, выполняется условие:

- f(x,y)< f(х₀,у₀) – max

- f(x,y)>f(х₀,у₀) – min

Необходимые условия экстремумов:

Если точка (х₀,у₀) – точка экстремума функции z=f(x,y) и в ней существуют обе частные производные, то производные в точке (х₀,у₀) равны нулю.

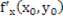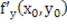=0 =0

10.Ф-лы , которые служат для предоставления опытных данных называются эмпирическими. В большинстве случаев хар-р зависимости между переменными предполагается известным и остаётся только опред-ть пар-ры самой ф-лы.

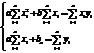
Получаемая система назв. «нормальной системой выравнивание эмпирических данных» по методу наим. квадратов вдоль прямой. Решая эту систему получаем значение параметров a и b, при кот. ф-я Ф’ab достигает минимума и прямая y=kx+b будет проведена наилучшим образом. Проведем группировку относительно a,b,c.

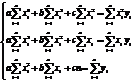получ. сист. наз. «норм. сист. выравн. эмпирич. Данных по методу наим. квадр. вдоль параболы».

Решая ее получаем значение a,b,c, которые доставляют минимум ф-и Ф от a,b,c, и для которых парабола y=ax²+bx+c будет проведена и наилучшим образом.

Аналогичным способом могут быть установл. и др. виды зависимости между данными эмпирического поля.

11. Первообразная ф-ии. Св-ва ∫. таблица

Опред-ие 1:Ф-ия F(x)-первообразная для ф-ии f(x) на некотором промежутке, если для всех х из этого промежутка выполняется рав-во F’(x)= f(x)

Опред-ие 2: Семейство всех п-ых для ф-ии f(x) на некотором промежутке называется неопределённым интегралом от ф-ии f(x) на это промежутке и обозначается

∫ f(x)dx=F(x)+c

Иначе неопределенный интеграл от ф-и это совокупность всех первообр. для этой функции.

Свойствa: 1.производная от неопределенного интеграла равна подынтегральной ф-и, которая явл. критерием правильности вычисления неопр. интеграла. (∫f(x)dx)’=(F(x)+C)’=f(x)

2. Неопр. интеграл от алгебраической суммы двух или более ф-й равен алгебр. cумме неопр. интегралов от этих ф-й. ∫=∫₁+∫₂

3. Постоянный множитель можно вынести за знак неопр. интеграла. ∫kf(x)dx=k∫f(x)dx

Таблица основных интегралов:

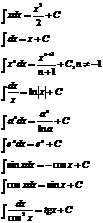
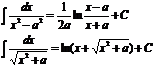
12. Замена переменной в неопред-ом интеграле.

Т-ма1: Пусть дано ∫f(x)dx=F(x)+c (1)

Предположим x=φ(t),тогда ∫f(φ(t))* φ’t(dt)= F(φ(t))+c (2)

Предполагается , что ф-ии f(x), φ(t) непрерывны.

Док-во: По данному F(x)-первообразная для f(x) → F’(x)=f(x). Требуется док-ть рав-во (2), что F(φ(t)) явл-ся первообразной для f(φ(t))*φ’(t). Воспользуемся теоремой о производной сложной ф-ии:

(F(φ(t)))’=F’(φ(t))* φ’(t)= f(φ(t))*φ’(t)

Замечание: Пусть требуется вычислить ∫(1). Если ф-ию F(φ(t)) найти легче, чем F(x), то в рав-ве (1) полагают x=φ(t) и находят ф-ию F(φ(t)). Затем осуществляется переход к старой переменной х и получается искомая ф-ия F(x).

Интегрирование по частям:

Теорема:Пусть ф-ия U(x),V(x) непрерывны вместе со своими производными U’(x),V’(x), тогда на этом промежутке имеет место рав-во:

∫UdV=UV-∫VdU –ф-ла интегрирования по частям.

Она применяется , если ∫VdUвычислить легче, чем ∫UdV

Замечание : Ф-ла (1) применяется для интегрирования выраж-ий след-его вида:

1. ∫Pn(x)sinxdx

2. ∫(Pn(x)cosxdx

3. ∫(Pn(x)a^xdx

4. ∫(Pn(x)ln^m(x)dx

5. ∫(Pn(x)arctgxdx

6. ∫(Pn(x)arcsinxdx

13. Интегрирование простых дробей

Прост. дробями наз. ф-и след вида:

1. A\(x-a), 2. A\(x-a)ⁿ, 3. Mx+N\(x²+px+q), 4. Mx+N\(x²+px+q)^m,

Где m,n- натуральные числа >1,.

a,p,q,A,M,N – любые действит. числа.

D=p²-4q<0

Дроби вида 1, 2 интегрируются непосредственно.

1.∫A/(x-a)dx=A∫d(x-a)/(x-a)=Aln|x-a|+c

2. ∫ A\(x-a)ⁿ=A∫(x-a)^-nd(x-a)=A(x-a)^-n+1/(-n+1)+C

3. Выделение полного квадрата:

∫4x+1\(x²+x+1)dx=∫(4x+1)dx/((x+1\2)²+3\4)=∫x+1/2=t, x=t-1/2, dx=(t-1/2)’dt, dx=dt]= =∫(4(t-1\2)+1)\(t²+3\4)dt=∫(4t-1)\(t²+3\4)dt=∫4t\(t²+3\4)dt-∫dt\t²+3\4)=2ln(t²+3\4)-1\(/3\2)arctgt\(/3\2)+C=2ln(x²+x+1)-2\(/3)arctg((2x+1)\/3)+C

Выражение, кот. содержат квадратный трех член Ax+B\ax²+bx+c; Ax+B\/(ax²+bx+c) так же интегрируем выделением полного квадрата трехчлена.

14. Интегрирование рациональных дробей

Опред-ие 1:Рац-ая дробь – отношение двух многочленов P(x)|Q(x), где P и Qимеют действительные коэффициенты.

Опред-ие 2:Рац-ая дробь – правильная, если степень многочлена , стоящего в числительном ниже степени многочлена , стоящего в знаменатиле. В противном случае дробь наз-ся неправильной.

Любую неправильную рац-ую дробь можно представить путём деления суммы многочленов и правильной рациональной дроби.

Теорема о разложении прав. рац. дроби на прост. дроби.

Пусть P(x)\Q(x) – прав. рац. дробь причем знаменатель представлен в виде:

Q(x)=(x-a)ⁿ…(x²+px+q)^m.

Тогда прав. рац. дробь можно представить в виде суммы простых дробей след. образом:

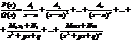
Где a,p,q – действ. числа, p²-4q<0:

A₁, A₂,..,A_n; N₁, N₂, Mm, Nm- неизвестные коэффициенты

2.

Теорема (необходимое и достаточное условие постоянства функции):

Пусть у=f(х) определена и непрерывна на множестве Х и внутри этого множества имеет конечную производную f’(x), на границе множества сохраняет непрерывность, если принадлежит Х.

Для того, чтобы f(x) была const на множестве Х, необходимо, чтобы f’(x)=0 внутри множества Х.

Достаточные условия возрастания и убывания функции:

Для того, чтобы f(x) была возрастающей (убывающей), достаточно чтобы f’(x)>0 (f’(x)<0) для всех х, принадлежащих множеству Х.

3.

1ое достаточное условие экстремума функции:

Пусть х₀ – критическая точка 1ого рода. Предположим, что у=f(x) дифференцируема в некоторой окрестности (х₀-δ,х₀+δ) и f’(x) сохраняет свой знак слева и справа от х₀.

Значит: если при переходе через х₀ f’(x) меняет знак с + на -, то в т. х₀ f(x) имеет максимум, если с – на +, то минимум, если знак не меняется, то х₀ не является экстремумом.

2ое достаточное условие экстремума функции:

Пусть х₀ – стационарная точкам, в которой f(x) дважды дифференцируема, тогда если f”(х)<0, то х₀ – максимум, f”(х)>0, то х₀ – минимум (если равно 0, то не работает).

4.______

Пусть у=f(x) дифференцируема на (а,в), графиком ее является некоторая кривая.

Выпуклость кривой:Кривая у=f(x) называется выпуклой на (а,в), если все точки кривой лежат ниже любой ее касательной на этом интервале.

Вогнутость кривой:Кривая у=f(x) называется вогнутой на (а,в), если все точки кривой лежат выше любой ее касательной на этом интервале.

Точки перегиба:Точки, в которых выпуклость сменяется на вогнутость и наоборот, называются точками перегиба.

Теорема (достаточное условие выпуклости/вогнутости):

Пусть у=f(x) дважды дифференцируема на промежутке (а,в), тогда:

Если на (а,в) f”(x)>0, то кривая вогнутая;

Если на (а,в) f”(x)<0, то кривая выпуклая.

Теорема (достаточное условие перегиба):

Пусть х₀ – критическая точка 2ого рода, тогда:

Если при переходе через т. х₀ f” меняет знак с + на -, то х₀ – т. перегиб

Если с – на +, то выпуклость на вогнутость.

7.Понятие функции нескольких переменных:

Рассмотрим множество D, состоящее из пар действительных чисел (х,у). Любую пару чисел можно изобразить на плоскости точкой.

Если каждой паре действительных чисел соответствует одно определенное число z?Z, то говорят, что на множестве D задана функция z=f(x,y) со значениями во множестве Z.

Функцию z=f(x,y) называют функцией двух переменных, а переменные х и у – независимыми переменными.

Определение предела и непрерывности функции двух переменных:

Пусть функция f(x,y) определена внутри некоторой окрестности точки (х₀,у₀) кроме, может быть, самой точки.

Число А называется пределом функции z=f(x,y) в точке М₀ (х₀,у₀), если для любой последовательности точек {(x_n,y_n)} области определения функции, отличных от (х₀,у₀) и сходящихся к (х₀,у₀), последовательность значений функции {(x_n,y_n)} сходится к А:

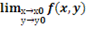=A.

Если 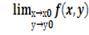=f(х₀,у₀), то функция f(x,y) называется непрерывной в точке (х₀,у₀).

8.Частные производные функции нескольких переменных:

Если существует предел

,

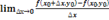
то он называется частной производной функции zпо х в точке 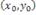и обозначается символами или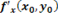

.

Аналогично определяется частная производная по у: = =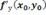

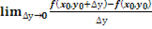
Полный дифференциал функции нескольких переменных:

Полным дифференциалом функции z=f(x,y) называется выражение вида dz = 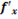(x,y)dx + 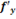(x,y)dy, где dx=∆х, dy=∆у.

Является суммой частных дифференциалов.

9.Экстремум функции нескольких переменных:

Функция z=f(x,y) имеет в точке М₀ (х₀,у₀) максимум (минимум) f(х₀,у₀), если вблизи этой точки для всех точек М, отличных от М₀, выполняется условие:

- f(x,y)< f(х₀,у₀) – max

- f(x,y)>f(х₀,у₀) – min

Необходимые условия экстремумов:

Если точка (х₀,у₀) – точка экстремума функции z=f(x,y) и в ней существуют обе частные производные, то производные в точке (х₀,у₀) равны нулю.

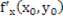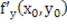=0 =0

10.Ф-лы , которые служат для предоставления опытных данных называются эмпирическими. В большинстве случаев хар-р зависимости между переменными предполагается известным и остаётся только опред-ть пар-ры самой ф-лы.

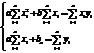
Получаемая система назв. «нормальной системой выравнивание эмпирических данных» по методу наим. квадратов вдоль прямой. Решая эту систему получаем значение параметров a и b, при кот. ф-я Ф’ab достигает минимума и прямая y=kx+b будет проведена наилучшим образом. Проведем группировку относительно a,b,c.

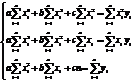получ. сист. наз. «норм. сист. выравн. эмпирич. Данных по методу наим. квадр. вдоль параболы».

Решая ее получаем значение a,b,c, которые доставляют минимум ф-и Ф от a,b,c, и для которых парабола y=ax²+bx+c будет проведена и наилучшим образом.

Аналогичным способом могут быть установл. и др. виды зависимости между данными эмпирического поля.

11. Первообразная ф-ии. Св-ва ∫. таблица

Опред-ие 1:Ф-ия F(x)-первообразная для ф-ии f(x) на некотором промежутке, если для всех х из этого промежутка выполняется рав-во F’(x)= f(x)

Опред-ие 2: Семейство всех п-ых для ф-ии f(x) на некотором промежутке называется неопределённым интегралом от ф-ии f(x) на это промежутке и обозначается

∫ f(x)dx=F(x)+c

Иначе неопределенный интеграл от ф-и это совокупность всех первообр. для этой функции.

Свойствa: 1.производная от неопределенного интеграла равна подынтегральной ф-и, которая явл. критерием правильности вычисления неопр. интеграла. (∫f(x)dx)’=(F(x)+C)’=f(x)

2. Неопр. интеграл от алгебраической суммы двух или более ф-й равен алгебр. cумме неопр. интегралов от этих ф-й. ∫=∫₁+∫₂

3. Постоянный множитель можно вынести за знак неопр. интеграла. ∫kf(x)dx=k∫f(x)dx

Таблица основных интегралов:

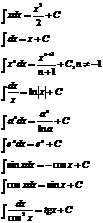
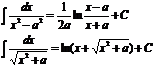
12. Замена переменной в неопред-ом интеграле.

Т-ма1: Пусть дано ∫f(x)dx=F(x)+c (1)

Предположим x=φ(t),тогда ∫f(φ(t))* φ’t(dt)= F(φ(t))+c (2)

Предполагается , что ф-ии f(x), φ(t) непрерывны.

Док-во: По данному F(x)-первообразная для f(x) → F’(x)=f(x). Требуется док-ть рав-во (2), что F(φ(t)) явл-ся первообразной для f(φ(t))*φ’(t). Воспользуемся теоремой о производной сложной ф-ии:

(F(φ(t)))’=F’(φ(t))* φ’(t)= f(φ(t))*φ’(t)

Замечание: Пусть требуется вычислить ∫(1). Если ф-ию F(φ(t)) найти легче, чем F(x), то в рав-ве (1) полагают x=φ(t) и находят ф-ию F(φ(t)). Затем осуществляется переход к старой переменной х и получается искомая ф-ия F(x).

Интегрирование по частям:

Теорема:Пусть ф-ия U(x),V(x) непрерывны вместе со своими производными U’(x),V’(x), тогда на этом промежутке имеет место рав-во:

∫UdV=UV-∫VdU –ф-ла интегрирования по частям.

Она применяется , если ∫VdUвычислить легче, чем ∫UdV

Замечание : Ф-ла (1) применяется для интегрирования выраж-ий след-его вида:

1. ∫Pn(x)sinxdx

2. ∫(Pn(x)cosxdx

3. ∫(Pn(x)a^xdx

4. ∫(Pn(x)ln^m(x)dx

5. ∫(Pn(x)arctgxdx

6. ∫(Pn(x)arcsinxdx

13. Интегрирование простых дробей

Прост. дробями наз. ф-и след вида:

1. A\(x-a), 2. A\(x-a)ⁿ, 3. Mx+N\(x²+px+q), 4. Mx+N\(x²+px+q)^m,

Где m,n- натуральные числа >1,.

a,p,q,A,M,N – любые действит. числа.

D=p²-4q<0

Дроби вида 1, 2 интегрируются непосредственно.

1.∫A/(x-a)dx=A∫d(x-a)/(x-a)=Aln|x-a|+c

2. ∫ A\(x-a)ⁿ=A∫(x-a)^-nd(x-a)=A(x-a)^-n+1/(-n+1)+C

3. Выделение полного квадрата:

∫4x+1\(x²+x+1)dx=∫(4x+1)dx/((x+1\2)²+3\4)=∫x+1/2=t, x=t-1/2, dx=(t-1/2)’dt, dx=dt]= =∫(4(t-1\2)+1)\(t²+3\4)dt=∫(4t-1)\(t²+3\4)dt=∫4t\(t²+3\4)dt-∫dt\t²+3\4)=2ln(t²+3\4)-1\(/3\2)arctgt\(/3\2)+C=2ln(x²+x+1)-2\(/3)arctg((2x+1)\/3)+C

Выражение, кот. содержат квадратный трех член Ax+B\ax²+bx+c; Ax+B\/(ax²+bx+c) так же интегрируем выделением полного квадрата трехчлена.

14. Интегрирование рациональных дробей

Опред-ие 1:Рац-ая дробь – отношение двух многочленов P(x)|Q(x), где P и Qимеют действительные коэффициенты.

Опред-ие 2:Рац-ая дробь – правильная, если степень многочлена , стоящего в числительном ниже степени многочлена , стоящего в знаменатиле. В противном случае дробь наз-ся неправильной.

Любую неправильную рац-ую дробь можно представить путём деления суммы многочленов и правильной рациональной дроби.

Теорема о разложении прав. рац. дроби на прост. дроби.

Пусть P(x)\Q(x) – прав. рац. дробь причем знаменатель представлен в виде:

Q(x)=(x-a)ⁿ…(x²+px+q)^m.

Тогда прав. рац. дробь можно представить в виде суммы простых дробей след. образом:

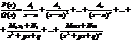
Где a,p,q – действ. числа, p²-4q<0:

A₁, A₂,..,A_n; N₁, N₂, Mm, Nm- неизвестные коэффициенты

Интегрирование некоторых иррациональных ф-ий

Рассмотрим интеграл вида:

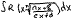
Где подинтегральная ф-ия – рац-ая по переменной х

п- натуральное число; a,b,c,d- некоторые постоянные.

∫-лы такого вида могут быть вычислены способом подстановки :

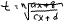
Таким образом:

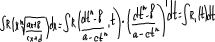
Под интегралом получили рациональную дробь.

Частные случаи:

1. c=0, d=1→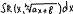

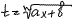
2. a=1, b=0, c=0,d=1

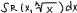
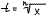
17. Геометрическая задача. Определение опред-ого интеграла.

Пусть ф-я y=f(x) опред. И непрерывна на [a;b]. Продел. следующие операции:

1. отрезок [a;b] разобьем на n-частей (не обяз. равных) точками.

a=x₀<x₁<x₂<…<x_k<x_k+1<…<x_n=b

2. На кажд. k-ом отрезке выберем x_k0[x_k,x_k+1] и найдем значение ф-и в них.

3. Обозначим через l_k длину k-того отрезка l_k=| x_k+1- x_k|б а через l max l_k. l=(max l_k) 0≤k≤n-1

4. Составим произведение: f(x_k)l_k=f(x_k)(x_k+1) и найдем сумму всех таких произведений 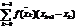- сумма Римана.

5. найдем предел суммы Римана

Определение определ-ого ∫:

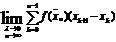
Если этот предел сущ. и конечен, ни зависящий ни от способа дробления, ни от выбора точек в соответствующих частичных промежутках ,то его наз. определ. интегралом от ф-и f(x) по отрезку [a;b] и обознач. след. символов:

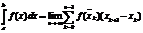
Если ф-я f(x) непрерывна или кусочнонепрерывна на [a;b], то она интегрируема на нем, т.е. ее опред. интеграл сущ.

18. Свойства определённых ∫-ов.

1) Определённый ∫ есть число, которое зависит от вида интегральной ф-ии и от пределов интегрирования, но не зависит от переменной интегрирования, поэтому можно обозначать любой буквой.

2) определенным ∫-ом явл-ся ∫ когда нижний предел меньше верхнего : a<b

если же a>b, то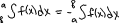

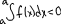
3).Постоянный множитель можно выносить за знак ∫:

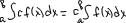
4). Опред-ый ∫ от алгебраической суммы функций равен алгебраической сумме отрезков интегралов:

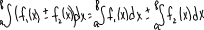
5).при любом расположении точек a,b,c справедливо рав-во

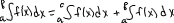
6). Если m и M соответственно наименьшее и наибольшее значения ф-ии на [a;b] и a<b, то

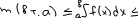
7) теорема о среднем значении:

Если f(x) непрерывна на [a;b] , то на этом отрезке обязательно найдётся такая точка ξ, что