Модуль 2: Функции многих переменных
Лекции
Лекции 13-14. Функции нескольких переменных как отображения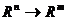 
. Скалярные и векторные функции. График функции нескольких переменных. Примеры функций нескольких переменных и их геометрическое представление. Линии и поверхности уровня. Окрестности, открытые и замкнутые множества в 
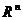. Линейно связные множества, области. Предел и непрерывность функции нескольких переменных. Свойства функций, непрерывных на ограниченном и замкнутом множестве Rn.
ОЛ-3 гл. 8, §1-4, ОЛ-5 гл.8 §1-3, 11, 12, ОЛ-12 гл.1.
Лекция 15. Частные производные и частные дифференциалы скалярной функции нескольких переменных и их геометрическая интерпретация. Понятие дифференцируемости функции. Необходимые и достаточные условия дифференцируемости.
ОЛ-3 гл. 8, §5, 6, ОЛ-5 гл.8 §4, 5, ОЛ-12 гл.2.
Лекция 16. Частные производные и дифференциалы высших порядков скалярной функции. Матрица Гессе. Теорема о независимости смешанной производной от последовательности выполнения дифференцирования.
ОЛ-3 гл. 8, §5, 6, ОЛ-5 гл.8 §4, 5, ОЛ-12 гл. 3.
Лекция 17. Полный дифференциал. Необходимые и достаточные условия, при которых дифференциальная форма является полным дифференциалом. Дифференцируемость сложной функции. Инвариантность формы первого дифференциала. Дифференциалы высших порядков.
ОЛ-3 гл. 8, §7-10; ОЛ-5 гл.8 §6-9, ОЛ-12 гл.2.6, 2.7.
Лекции 18-19. Неявно заданные функции. Теорема о существовании и дифференцируемости неявно заданной функции. Производная по направлению скалярной функции нескольких переменных. Градиент функции и его свойства. Уравнения касательной и нормали к линии уровня для функции двух переменных. Касательная плоскость и нормаль к поверхности. Формула Тейлора для функции двух и n переменных.
ОЛ-3 гл. 8, §10, 11, 14, 15, 17; ОЛ-5 гл.8 §7, 8, 9, 13 -16, ОЛ-12 гл. 4, 5, 3.4.
Лекция 20. Локальный экстремум скалярной функции нескольких переменных. Необходимое условие локального экстремума непрерывно дифференцируемой функции. Достаточное условие локального экстремума дважды непрерывно дифференцируемой функции. Примеры для функции двух переменных.
ОЛ-3 гл. 8, § 17; ОЛ-5 гл.8 §16-18, ОЛ-12 гл. 6.
Лекция 21. Условный экстремум скалярной функции двух переменных. Функция Лагранжа. Необходимое и достаточное условия существования условного экстремума. Нахождение наибольшего и наименьшего значений функции двух переменных в замкнутой области. Обобщение теории условного экстремума на скалярные функции n переменных.
ОЛ-3 гл. 8, § 18; ОЛ-5 гл.8 §19 ОЛ-12 гл.7.
Лекция 22. Частные производные и дифференцируемость векторной функции, ее полный дифференциал и матрица Якоби. Дифференцируемость сложной векторной функции. Теорема о неявной функции для векторных функций многих переменных. Теорема о существовании и дифференцируемости обратной для векторной функции.
ОЛ-12 гл. 1, 2, 4.
Лекции 23-24. Определенные интегралы, зависящие от параметра. Дифференцирование и интегрирование интегралов по параметру. Равномерная сходимость несобственных интегралов. Признаки равномерной сходимости несобственных интегралов. Непрерывность и дифференцируемость несобственных интегралов по параметру. Интегрирование несобственных интегралов по параметру.
ОЛ-1 гл. 8.
Упражнения
Занятия 15-16.Область определения ФНП. Линии и поверхности уровня. Предел и непрерывность ФНП. Частные производные первого порядка.
Ауд. ОЛ-8 гл.7: 7.6 7.8 7.10 7.19 7.21 (в этих задачах также построить линии и поверхности уровня); 7.12 7.14 7.15 7.18 7.32 7.35 7.38 7.39 7.41 7.43 7.44 7.46 7.50 7.52; 7.55 7.57 7.61 7.63 (только производные 1-го порядка) или: ОЛ-10: 1792(в) 1793(г) 1795(а) 1796(в) 1797(б, в) 1799(в) 1803 1805 1807 1812
Дома. ОЛ-8 гл.7: 7.7 7.9 7.13 7.20 (в этих задачах также построить линии и поверхности уровня) 7.33 7.34 7.45 7.47 7.51; 7.56 7.58 7.60 7.62 7.64 (только производные 1-го порядка) или: ОЛ-10: 1792(е, и) 1793(б, в) 1794(г, ж) 1796(а, б) 1797(г, е) 1799(б) 1804 1806 1810 1813
Занятие 17.Частные производные высших порядков. Дифференциалы первого и второго порядков ФНП.
Ауд. ОЛ-8 гл.7: 7.65 7.66 7.70 7.87 7.89 7.91 7.103 7.105 или: ОЛ-10: 1892 1894 1897 1834 1838 1844 1917 1925
Дома. ОЛ-8 гл.7: 7.67 7.68 7.71 7.88 7.90 7.92 7.102 7.107 или: ОЛ-10: 1891 1893 1898 1838 1840 1845 1016 1925
Занятия 18-19.Восстановление функции по ее полному дифференциалу. Производная сложной и неявной функции.
Ауд. ОЛ-9 гл.9: 9.98 - 9.104 (четн.), ОЛ-8 гл. 7: 7.114 7.119 7.122 7.129 7.135 7.141 7.145 7.149 7.150 7.157 7.161 или: ОЛ-10: 1926 1928 1930 2803 2806 1856 1861 1864 1865 1870 1944 1946 1948 1950 1955
Дома. ОЛ-9 гл.9: 9.99 - 9.105 (неч.), ОЛ-8 гл. 7: 7.116 7.118 7.123 7.130 7.136 7.140 7.146 7.150 7.151 7.158 7.160 или:
ОЛ-10: 1927 1929 1931 2802 2804 1857 1862 1863 1871 1943 1947 1949
Занятия 20-21.Производная по направлению и градиент ФМП. Касательная плоскость и нормаль к поверхности. Экстремум ФМП.
Ауд. ОЛ-8 гл. 7: 7.229(а) 7.233(а) 7.232 7.234 7.239(а) 7.187-7.195 (неч.), ОЛ-9 гл.10: 10.31-10.43 (неч.) или: ОЛ-10: 1876 1878 1882(а) 1886 1889 1981(а) 1982 1985 1986 2008 2010 2012 2016 2016.1 (1999 2001 2003)
Дома. ОЛ-8 гл. 7: 7.229(б) 7.233(б, в) 7.235 7.239(б) 7.188-7.194(четн.) (7.179 7.183 7.184), ОЛ-9 гл. 10:10.32-10.44 (четн.) или: ОЛ-10: 1877 1879 1882(б) 1883 1888 1981(б) 1984 1987 1990 2009 2011 2014 2016.2 (1997 2002 2004)
Занятие 22.Условный экстремум ФМП.
Ауд. ОЛ-10: 2021-2024 2031 или
ОЛ-8 гл. 7: 7.201-7.205 7.214.
Дома. ОЛ-8 гл. 7: 7.206-7.209, 7.213.
Занятие 23-24.Интегралы с параметрами.
Ауд. ОЛ-1 гл. 8: 8.1 (а, б) 8.3 (а, б) 8.4 8.6 (а) 8.7
Дома. ОЛ-1 гл. 8: 8.1 (в) 8.3 (в) 8.5 8.6 (б) 8.8
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних заданий, подготовке к контрольным работам и рубежным контролям.