Структура диалога пользователя в системе STATISTICA

Структура диалога пользователя в каждом статистическом модуле имеет об­щие черты:

1) после выбора из переключателя модулей (рис. 7.3) открывается стартовая па­нель выбранного статистического модуля;

2) далее необходимо открыть файл данных и выбрать переменные для анализа из открытого файла;

3) затем выбираются метод анализа и конкретная вычислительная процедура с со­ответствующими параметрами расчета из меню в стартовой панели модуля;

4) далее запускается вычислительная процедура. Если процедура итерационная, то система дает возможность на каждом шаге просмотреть результаты в появив­шемся на экране окне и при необходимости добавить число итераций для увели­чения точности оценок;

5) используя графические возможности и специальные таблицы вывода с вычис­ленными разнообразными статистиками, можно осуществить всесторонний про­смотр и анализ результатов;

6) выбирается следующий шаг анализа.

В сложном проекте следует работать с различными модулями, последова­тельно переключаясь между ними.

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ...

Примеры использования системы STATISTICA

Расчет основных характеристик случайных величин

Запускаем систему STATISTICA и выбираем статистический модуль Basic Statistics/Tables (Основные статистики и таблицы). Создаем новый файл исход­ных данных, выбирая из меню пункт File/New data, и присваиваем ему произвольное имя, например exampM.sta.

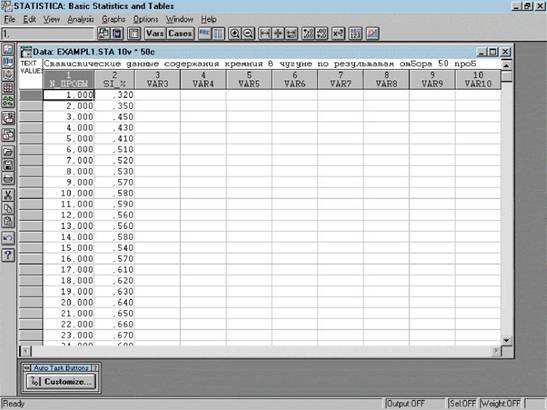Рис.7.4. В рабочем окне системы STATISTICA расположен файл с исходными данными содержания кремния в чугуне

Исходные данные для анализа возьмем из примера 3.8, в котором приведены результаты обработки 50 проб передельного чугуна на предмет содержания в них кремния (табл. 3.7). Заполним таблицу в системе STATISTICA с исходными данны­ми, как показано на рис. 7.4. Для этого создаем две переменные: первая содержит номер пробы чугуна (NJlPOBbl), вторая - процентное содержание кремния в чугуне для соответствующей пробы (Sl_%). Размер таблицы в системе по умолчанию при­нят 10 на 10 (10 переменных с именами VAR1, VAR2, ..., VAR10 и 10 случаев). Чтобы изменить имя переменной, необходимо выбрать пункт меню Edit/Variables/Current Specs или нажать комбинацию клавиш [Ctrl]+[F2], а затем в диалоге указать нужное имя.

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ...

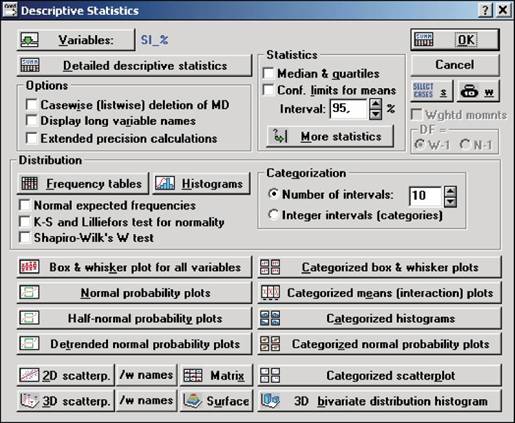Рис.7.5.Вид экрана меню Descriptive Statistics (Описательные статистики)

После того как подготовлен файл исходных данных, выбираем пункт меню Analysis/Descriptive Statistics (Описательная статистика). В появившемся диалого­вом окне, вид которого показан на рис. 7.5, следует выбрать переменную для анали­за нажатием кнопки Variables. Мы выбрали переменную, содержащую данные о про­центном содержании кремния в чугуне, имя выбранной переменной отражается ря­дом с кнопкой Variables. Диалог Описательная статистика позволяет: - вычислить разнообразные выборочные характеристики (Statistics): Median&quartiles - медиана и квартили, Conf. Limits for means - доверительные границы для среднего. В строке Alpha error можно задать требуемый уровень значимости. Напомним, что уровень значимости - это вероятность неправильного отвержения гипотезы, когда она верна (подробнее см. п. 3.3). Более расширен­ный набор статистик для расчета можно выбрать нажатием кнопки More statistics (рис. 7.6): Mean - среднее арифметическое, Sum - сумма, Median - медиана, Standard Deviation - стандартное отклонение, Variance - дисперсия, Minimum&maximum - минимум и максимум, Range - размах, т.е. разность между максимумом и минимумом, Skewness - коэффициент асимметрии, Kurtosis - ко­эффициент эксцесса:

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ…

ок

UU

Default

F Valid N |7 Mean Sum Median W Standard Deviation Variance Standard error of mean Э5Х confidence limits of mean W Minimum & maximum Lower & upper quartiles Range Qjjartile range Skewness Kurtosis Standard error of skewness Standard error of kurtosis Other descriptive statistics including mode, harmonic means, user-specified percentiles, etc. are available in the Descriptive Statistics option in the Nonparametrics module.

построить для выборки таблицу частот (Frequency Tables) и гистограмму частот (Histograms); отметив пункт Normal expected frequencies, можно нанести на гис­тограмму кривую нормального распределе­ния и визуально оценить соответствие ис-

Г 952 confidence limits of mean ХОДНЫХ ДЭННЫХ НОрМЭЛЬНОМу ЗЭКОНу рЭС-

W Minimum Ь maximum ПредеЛвНИЯ;

- проверить гипотезу о нормальности рас­пределения наблюдаемых случайных ве­личин с использованием критерия Колмо­горова-Смирнова, выбирая его в разделе Distribution.

Рис.7.6. Меню Статистики

Для визуализации результатов имеется возможность построения разнообразных гра­фиков, вызываемых нажатием соответствую­щей кнопки в нижней части экрана. Результаты статистического анализа выводятся в специальное окно. Для дан­ных из примера вид окна с результатами показан на рис. 7.7, из которых следует, что среднее арифметическое (математическое ожидание) содержания кремния в чугуне составляет 0,6504%; выборочная дисперсия 0,0185%; максимальное и минимальное значения равны соответственно 0,32 и 0,95%; действительное содержание кремния в чугуне с вероятностью 95% лежит в интервале от 0,6117 до 0,6891%. Заметим, что эти данные близки к результатам, полученным ранее в примере 3.8 с помощью паке­та Microsoft Excel, небольшие расхождения объясняются точностью представления результатов.

Рис.7.7. Вид окна с результатами расчета статистик из примера 3.8

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

Проверка нормальности распределения

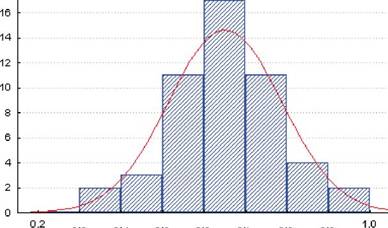
Проверим гипотезу о нормальности распределения данных из примера. Для этого в окне диалога Описательные статистики, показанного на рис. 7.5, отметим мышью пункт K-S test and Lilliefors test normality (Тест Колмогорова–Смирнова для проверки нормальности) и нажмем кнопку Histograms. В результате на экране поя­вится окно (рис. 7.8), на котором изображена гистограмма переменной Sl_% и до­полнительно нанесена линия нормального распределения. В верхней части гисто­граммы показан рассчитанный параметр теста Колмогорова - Смирнова - критерий D (см. п. 3.6).

X Graph!*: S\_%

П х

20 18

SM4

K-S d=,036

0.3 0.4 0.5 0,6 0,7 0,8 0,9

U р р е г В о и n d a ri es (х <= bounds ry)

Expected Normal

Puc.7.8. Гистограмма распределения содержания кремния в чугуне с результатами проверки гипотезы о нормальности распределения

Напомним, что критерий D называется критерием согласия, поскольку он про­веряет, в какой степени наблюдаемые значения случайной величины согласуются с функцией нормального распределения: чем меньше величина D, тем в меньшей степени эмпирическая функция распределения случайной величины отличается от нормальной функции распределения. В нашем случае критерий D=0,07934, следо­вательно, гипотеза о нормальности распределения данных о содержании кремния в

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

чугуне подтверждается. В противном случае система выдала бы соответствующее сообщение и выделила бы данный критерий отличительным цветом.

Регрессионный анализ

Применение системы STATISTICA для регрессионного анализа рассмотрим на примере исследования взаимосвязи среднемесячного удельного расхода кокса и со­ответствующей величины удельного выхода шлака по данным работы одной из до­менных печей ОАО "Магнитогорский металлургический комбинат" (ОАО ММК), кото­рые отражены в табл. 7.3. Напомним, что задача регрессионного анализа состоит в том, чтобы по наблюдениям входных (X) и выходных (Y) параметров:

- построить регрессионную модель (уравнение регрессии), т.е. оценить параметры модели (коэффициенты уравнения) наилучшим образом;

- построить доверительные интервалы для коэффициентов модели;

- проверить гипотезу о значимости регрессии;

- оценить степень адекватности модели и т.д.

Из теории доменного процесса известно, что величина расхода кокса зависит от выхода шлака, а не наоборот. Поэтому зависимой переменной Y будет являться величина удельного расхода кокса, а независимой переменной X - величина удель­ного выхода шлака. Регрессионный анализ будем проводить в несколько этапов.

Таблица 7.3

Фактические данные о расходе кокса (К) и выходе шлака (Ш) на одной из доменных печей ОАО ММК

№ п/п	к, кг/т чугуна	ш, кг/т чугуна	№ п/п	к, кг/т чугуна	ш, кг/т чугуна	№ п/п	к, кг/т чугуна	ш, кг/т чугуна

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

						Окончание табл. 7.3

1. Воспользуемся статистическим модулем Nonlinear estimation (Нелинейное оценивание), в котором создадим новый файл exampl2.sta и занесем в него данные из табл. 7.3. На рис. 7.9 показан файл с исходными данными. Переменные, содер­жащие данные об удельных расходе кокса и выходе шлака, обозначены соответст­венно KOKS и SLAG.

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

2. Последовательность регрессионного анализа в системе STATISTICA лучше

!& STATISTICA: В

Analysis Window

Рис. 7.9.Файл исходных данных для регрессионного анализа

всего начинать с визуальной оценки положения данных при помощи различных графических средств. Поскольку в нашем случае изучается зависимость типа Y=f(X), то для этой цели по­дойдет двумерный график Scatterplots из меню Graphs/Stats 2D Graphs. В появившемся диало­говом окне (рис. 7.10) выбираем переменные X и Y нажатием кнопки Variables. Имена выбран­ных переменных Var X (SLAG) и Var Y (KOKS) отображаются в окне диалога. В этом окне до­полнительно можно отметить тип графика (Graph Туре) - Regular, модель оценивания (FIT) - первоначально выберем Off, стиль графика (Style) - Normal, величину доверительного ин­тервала и т.д. После нажатия кнопки ОК на эк­ране в отдельном окне появляется построенный график.

3. Из анализа наблюдений положения данных на графике делаем вывод о пригодности для оценивания полиномиальной регрессионной модели. Отметим в диалоговом окне (рис. 7.10) модель оценивания Polynomial и нажмем кнопку ОК. В результате появится отдельное окно с графиком, в котором на точечные данные нанесена кривая, подобранная по методу наименьших квадратов и описываемая многочленом 5-го порядка (рис. 7.11). Уравнение много­члена представлено в заголовке графика и имеет следующий вид:

у = -73616,8 +1508,463 • х - 12,187 • х +0,049 • х -9,678-10 -х +7,619-10 -х .

Абсолютная величина каждого коэффициента в уравнении регрессии характе­ризует вклад соответствующей степенной составляющей на параметр отклика у.

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

2D Scatterplots

{Variables:

OK

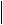
VarX: SLAG VarY: KOKS

Cancel

Options.

Graph Type:

FIT

Multiple Double Y ^j Frequency

Quantile \cf_ S

STYLE -Normal Polar Г Layered No of Freq: ff~\*

Logarithmic J_ Exponential Spline

I I___ *

v, Least Squares

^Neg Exp/Wght

ЙШ Custom Function

Custom: I none

rELLIPSE-f^Off С Normal Г Range	Coefficient:
I-95 Ш

.-CONFIDENCE BANDS
<* flff L I-

ГОп

Puc.7.10. Окно построения графиков для подгонки модели оценивания

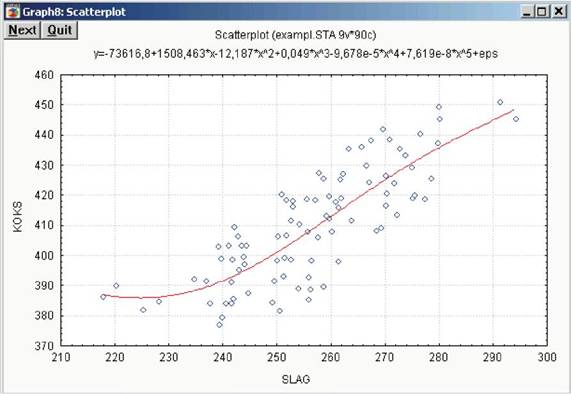
Рис.7.11.Полиномиальная кривая 5-го порядка, рассчи-танная по методу наименьших квадратов

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

4. Для того чтобы проанализировать регрессионную модель, из главного меню системы Analysis (Анализ) выбираем пункт User-specified regression (Определяемая пользователем регрессия). На экране появляется начальное диалоговое окно (рис. 7.12), в котором нажатием кнопки function to be estimated & loss function (функция оценивания и функция потерь) можно с помощью формул задать функцию, которую необходимо оценить, а также определить функцию потерь.

Рис. 7.12. Начальное окно диалога по оценке параметров определяемой пользователем регрессионной кривой

Рассмотрим в качестве примера в дальнейшем зависимость между удельным расходом кокса (KOKS) и удельным выходом шлака (SLAG) в виде полинома 3-й степени:

KOKS=bo+bi*SLAG+b2*SLAG²+ b3*SLAG³. Функция потерь по умолчанию задается в виде квадрата отклонения наблюдаемых от предсказанных с помощью регрессионной модели значений (OBS-PRED)².

5. Нажатие клавиши ОК приводит к появлению окна Model Estimation (Оцени-вание модели) для выбора метода и начальных установок для пользовательской регрессии (рис. 7.13). В качестве метода оценивания выберем квазиньютоновский. В методах нелинейного оценивания важно правильно подобрать начальные прибли­жения. Неизвестными параметрами модели являются коэффициенты bo, b-i, Ьг и Ьз. Нажав кнопку Start values (Начальные значения), в появившемся диалоговом окне введем начальные значения, предсказанные на основе предварительного графиче­ского анализа данных: bo=-73616, bi=1508, Ьг=-12 и Ьз=0,049. Нажатие клавиши ОК приводит к появлению окна оценок параметров модели на каждом шаге итерации. После того как оценивание завершится, внизу окна появится сообщение Parameter estimation process converged (Процесс оценивания параметров сошелся).

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

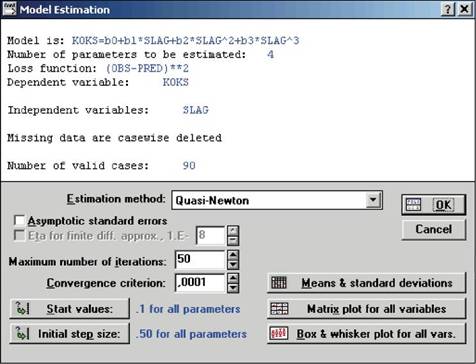
Рис. 7.13. Окно выбора метода и начальных установок для пользовательской регрессии

6. Далее нажимаем кнопку ОК, после чего открывается окно Results (Резуль­таты), показанное на рис. 7.14. Окно результатов имеет следующую структуру: верхняя часть окна - информационная, нижняя содержит функциональные кнопки, позволяющие всесторонне просмотреть результаты анализа.

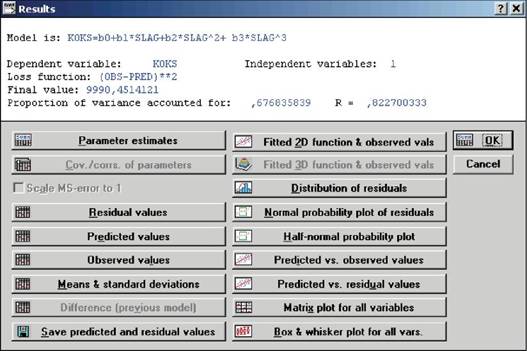
Рис. 7.14. Окно результатов оценивания параметров пользовательской регрессии

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

Информационная часть содержит краткую информацию о проведенном ана­лизе, а именно:

• Model is - вид модели оценивания. В нашем случае KOKS=bo+bi*SLAG+b2*SLAG²+ b3*SLAG³;

• Dependent variable - зависимая переменная. В нашем примере это удельный расход кокса (KOKS);

• Independent variables - количество независимых переменных. В примере не­зависимая переменная одна - удельный выход шлака;

• Loss function - вид функции потерь;

• Final value - последнее значение параметра, по которому система проводила подгонку модели.

Функциональные кнопки позволяют представить результаты в виде таблиц и графиков. Выберем кнопку Parameter estimates (Параметры оценивания), и на экра­не появится окно, в котором отражены численные значения коэффициентов модели (рис. 7.15). Нажатие кнопки Fitted 2D function & observed vals (Подогнанная функция и наблюдаемые значения) выводит на экран график результирующей кривой, нало­женной на наблюдаемые значения исходных данных (рис. 7.16). Таким образом, уравнение регрессионной модели окончательно примет вид

у = 4984,803-54,333-х +0,21035-х² -0,000265-х³.

Рис.7.15. Результаты расчета коэффициентов регрессионной модели

7. Далее следует оценить поведение остатков (residuals) модели, т.е. разно­стей между исходными (наблюдаемыми) значениями зависимой переменной и пред­сказанными с помощью модели. Исследуя остатки модели, можно оценить степень ее адекватности. С помощью функциональных кнопок в данном окне (см. рис. 7.14) можно проанализировать остатки как в графическом виде, так и в электронных таб­лицах.

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

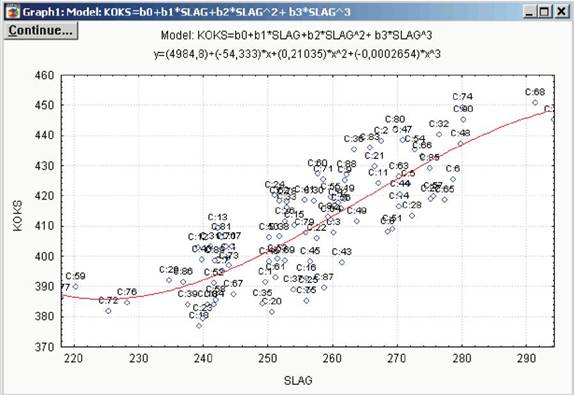
Рис.7.16. График результирующей регрессионной кривой, наложенной на наблюдаемые исходные данные

Сначала для оценки адекватности модели лучше всего использовать визу­альные методы и затем, если потребуется, перейти к статистическим. Нажмем кноп­ку Normal Probability plot of residuals (График остатков на нормальной вероятност-ной бумаге), и выбранная зависимость появится на экране в отдельном окне (рис. 7.17). Из графика остатков на нормальной вероятностной бумаге видно, что они дос­таточно хорошо ложатся на прямую, которая соответствует нормальному закону распределения. Поэтому гипотеза о нормальном распределении ошибок принимает­ся.

Далее нажмем кнопку Predicted vs. residual values (Распределение остатков), и на экране появится график следующего вида (рис. 7.18). Из этого графика видно, что остатки хаотично разбросаны на плоскости и в их поведении нет закономерно­стей. Нет основания говорить, что остатки коррелированы между собой. Следова­тельно, можно заключить, что регрессионная модель достаточно адекватно описы­вает данные.

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

Рис.7.17. График остатков на нормальной вероятностной бумаге

Рис.7.18. Распределение остатков на плоскости

7. КОМПЬЮТЕРНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ …

Контрольные вопросы

1. Какие преимущества дает экспериментатору использование средств вычисли­тельной техники?

2. Каковы возможности современных программ по обработке экспериментальных данных?

3. На каких принципах основана организация современных статистических пакетов?

4. Каким образом решается задача по оценке статистических характеристик с по­мощью пакета Microsoft Excel?

5. Как организовано взаимодействие пользователя с пакетом Statistica? Какие ос­новные модули он в себя включает?

6. Как определить коэффициенты уравнения регрессии, используя пакет Statistica?

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Белай Г.Е., Дембовский В.В., Саценко О.В. Организация металлургического эксперимента: Учеб. пособие для вузов / Под ред. В.В.Дембовского. - М.: Металлургия, 1993. - 256 с.

2. Теория и техника теплофизического эксперимента: Учеб. пособие для вузов / Ю.Ф.Гортышов, Ф.Н.Дресвянников, Н.С.Идиатуллин и др.; Под ред. В.КЩукина. - М.: Энергоатомиздат, 1985. - 360 с.

3. Кафаров В.В., Глебов М.Б. Математическое моделирование основных процессов химических производств: Учеб. для вузов. - М.: Высшая школа, 1991. - 400 с.

4. Львовский Е.Н. Статистические методы построения эмпирических формул: Учеб. пособие для вузов. - М.: Высшая школа, 1988. - 239 с.

5. Новицкий П.В., Зограф IA.A. Оценка погрешностей результатов измерений. -Л.: Энергоатомиздат, 1991. - 354 с.

6. Шинк X. Теория инженерного эксперимента: Пер. с англ. - М.: Мир, 1972. -381 с.

7. Налимов В.В, Голикова Т.Н. Логические основы планирования эксперимента. - М.: Металлургия, 1980. - 152 с.

8. Горский В.Г., Адлер ЮЛ. Планирование промышленных экспериментов. -М.: Металлургия, 1974. - 264 с.

9. Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. - М.: Машиностроение, 1985. -232 с.

10. Математическая статистика: Учеб. для вузов / В.Б.Горяинов, И.В.Павлов, ГМ.Цветкова, О.И.Тескин; Под ред. В.С.Зарубина, А.П.Крищенко. - М.: МГТУ им. Н.Э.Баумана, 2001. - 424 с.

11.Большее Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.

12. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере. -М.: ИНФРА-М, 1998. - 528 с.

13. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. - М.: Высшая школа, 2002 . - 479 с.

14.Гнеденко Б.В. Курс теории вероятностей. - М.: Наука, 1988. - 448 с.

15.Венцель Е.С., Овчаров Л Л. Теория вероятностей и ее инженерные

приложения. - М.: Наука, 1988. - 480 с. 16.Венцель Е.С. Теория вероятностей. - М.: Высшая школа, 1998. - 576 с. 17.Бендат Дж., Пирсол А. Прикладной анализ случайных данных. - М.: Мир,

1989. - 540 с. 18. Барский Л.А., Козин В.З. Системный анализ в обогащении полезных

ископаемых. - М.: Недра, 1978. - 486 с. 19.Кремер Н.Ш. Теория вероятностей и математическая статистика: Учеб. для

вузов. - М.:ЮНИТИ-ДАНА, 2000. - 541 с. 20.Гайдышев И. Анализ и обработка данных: Специальный справочник. - СПб.:

Питер, 2001. - 752 с. 21.Боровиков В.П. Популярное введение в программу STATISTICA. - М.:

КомпьютерПресс, 1998. - 267 с. 22.Боровиков В.П., Боровиков ИЛ. Statistica. Статистический анализ и

обработка данных в среде Windows. 2-е изд. - М.: Информационно-издательский дом ФИЛИНЪ. - 608 с. 23. Чекотовкий Э.В. Графический анализ статистических данных в Microsoft

Excel 2000. - М.; СПб; Киев: Диалектика, 2002. - 462 с. 24.Бородин А.Н. Элементарный курс теории вероятностей и математической

статистики: Учеб. для вузов. 3-е изд., испр. и доп. - СПб.: Издательство

"Лань”, 2002. - 356 с. 25. Боровков А.А. Математическая статистика. Оценка параметров, проверка

гипотез. - М.: Наука, 1984. - 312 с.

ПРИЛОЖЕНИЕ

Таблица П.1 Нормированная функция нормального распределения (функции Лапласа)

O(z)

V271

z

и²

j"e ² du

— ос

	Сотые доли Z
Z		0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0,5000	0,5040	0,5080	0,5120	0,5160	0,5199	0,5239	0,5279	0,5319	0,5359
0,1	0,5398	0,5438	0,5478	0,5517	0,5557	0,5596	0,5636	0,5675	0,5714	0,5753
0,2	0,5793	0,5832	0,5871	0,5910	0,5948	0,5987	0,6026	0,6064	0,6103	0,6141
0,3	0,6179	0,6217	0,6255	0,6293	0,6331	0,6368	0,6406	0,6443	0,6480	0,6517
0,4	0,6554	0,6591	0,6628	0,6664	0,6700	0,6736	0,6772	0,6808	0,6844	0,6879
0,5	0,6915	0,6950	0,6985	0,7019	0,7054	0,7088	0,7123	0,7157	0,7190	0,7224
0,6	0,7257	0,7291	0,7324	0,7357	0,7389	0,7422	0,7454	0,7486	0,7517	0,7549
0,7	0,7580	0,7611	0,7642	0,7673	0,7704	0,7734	0,7764	0,7794	0,7823	0,7852
0,8	0,7881	0,7910	0,7939	0,7967	0,7995	0,8023	0,8051	0,8078	0,8106	0,8133
0,9	0,8159	0,8186	0,8212	0,8238	0,8264	0,8289	0,8315	0,8340	0,8365	0,8389
1,0	0,8413	0,8438	0,8461	0,8485	0,8508	0,8531	0,8554	0,8577	0,8599	0,8621
1,1	0,8643	0,8665	0,8686	0,8708	0,8729	0,8749	0,8770	0,8790	0,8810	0,8830
1,2	0,8849	0,8869	0,8888	0,8907	0,8925	0,8944	0,8962	0,8980	0,8997	0,9015
1,3	0,9032	0,9049	0,9066	0,9082	0,9099	0,9115	0,9131	0,9147	0,9162	0,9177
1,4	0,9192	0,9207	0,9222	0,9236	0,9251	0,9265	0,9279	0,9292	0,9306	0,9319
1,5	0,9332	0,9345	0,9357	0,9370	0,9382	0,9394	0,9406	0,9418	0,9429	0,9441
1,6	0,9452	0,9463	0,9474	0,9484	0,9495	0,9505	0,9515	0,9525	0,9535	0,9545
1,7	0,9554	0,9564	0,9573	0,9582	0,9591	0,9599	0,9608	0,9616	0,9625	0,9633
1,8	0,9641	0,9649	0,9656	0,9664	0,9671	0,9678	0,9686	0,9693	0,9699	0,9706
1,9	0,9713	0,9719	0,9726	0,9732	0,9738	0,9744	0,9750	0,9756	0,9761	0,9767
2,0	0,9772	0,9778	0,9783	0,9788	0,9793	0,9798	0,9803	0,9808	0,9812	0,9817
2,1	0,9821	0,9826	0,9830	0,9834	0,9838	0,9842	0,9846	0,9850	0,9854	0,9857
2,2	0,9861	0,9864	0,9868	0,9871	0,9875	0,9878	0,9881	0,9884	0,9887	0,9890
2,3	0,9893	0,9896	0,9898	0,9901	0,9904	0,9906	0,9909	0,9911	0,9913	0,9916
2,4	0,9918	0,9920	0,9922	0,9925	0,9927	0,9929	0,9931	0,9932	0,9934	0,9936
2,5	0,9938	0,9940	0,9941	0,9943	0,9945	0,9946	0,9948	0,9949	0,9951	0,9952
2,6	0,9953	0,9955	0,9956	0,9957	0,9959	0,9960	0,9961	0,9962	0,9963	0,9964
2,7	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972	0,9973	0,9974
2,8	0,9974	0,9975	0,9976	0,9977	0,9977	0,9978	0,9979	0,9979	0,9980	0,9981
2,9	0,9981	0,9982	0,9982	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986	0,9986
3,0	0,9987	0,9987	0,9987	0,9988	0,9988	0,9989	0,9989	0,9989	0,9990	0,9990

Примечание. Ф(-2)=1-Ф(г)

Таблица П.2 Квантили нормированного нормального распределения z_p порядка Р

и2

z

V271

fe ² du = P

— ос

P	Тысячные доли Р
0,50	0,000	0,003	0,005	0,008	0,010	0,013	0,015	0,018	0,020	0,023
0,51	0,025	0,028	0,030	0,033	0,035	0,038	0,040	0,043	0,045	0,048
0,52	0,050	0,053	0,055	0,058	0,060	0,063	0,065	0,068	0,070	0,073
0,53	0,075	0,078	0,080	0,083	0,085	0,088	0,090	0,093	0,095	0,098
0,54	0,100	0,103	0,105	0,108	0,111	0,113	0,116	0,118	0,121	0,123
0,55	0,126	0,128	0,131	0,133	0,136	0,138	0,141	0,143	0,146	0,148
0,56	0,151	0,154	0,156	0,159	0,161	0,164	0,166	0,169	0,171	0,174
0,57	0,176	0,179	0,181	0,184	0,187	0,189	0,192	0,194	0,197	0,199
0,58	0,202	0,204	0,207	0,210	0,212	0,215	0,217	0,220	0,222	0,225
0,59	0,228	0,230	0,233	0,235	0,238	0,240	0,243	0,246	0,248	0,251
0,60	0,253	0,256	0,259	0,261	0,264	0,266	0,269	0,272	0,274	0,277
0,61	0,279	0,282	0,285	0,287	0,290	0,292	0,295	0,298	0,300	0,303
0,62	0,305	0,308	0,311	0,313	0,316	0,319	0,321	0,324	0,327	0,329
0,63	0,332	0,335	0,337	0,340	0,342	0,345	0,348	0,350	0,353	0,356
0,64	0,358	0,361	0,364	0,366	0,369	0,372	0,375	0,377	0,380	0,383
0,65	0,385	0,388	0,391	0,393	0,396	0,399	0,402	0,404	0,407	0,410
0,66	0,412	0,415	0,418	0,421	0,423	0,426	0,429	0,432	0,434	0,437
0,67	0,440	0,443	0,445	0,448	0,451	0,454	0,457	0,459	0,462	0,465
0,68	0,468	0,470	0,473	0,476	0,479	0,482	0,485	0,487	0,490	0,493
0,69	0,496	0,499	0,502	0,504	0,507	0,510	0,513	0,516	0,519	0,522
0,70	0,524	0,527	0,530	0,533	0,536	0,539	0,542	0,545	0,548	0,550
0,71	0,553	0,556	0,559	0,562	0,565	0,568	0,571	0,574	0,577	0,580
0,72	0,583	0,586	0,589	0,592	0,595	0,598	0,601	0,604	0,607	0,610
0,73	0,613	0,616	0,619	0,622	0,625	0,628	0,631	0,634	0,637	0,640
0,74	0,643	0,646	0,650	0,653	0,656	0,659	0,662	0,665	0,668	0,671
0,75	0,674	0,678	0,681	0,684	0,687	0,690	0,693	0,697	0,700	0,703
0,76	0,706	0,710	0,713	0,716	0,719	0,722	0,726	0,729	0,732	0,736
0,77	0,739	0,742	0,745	0,749	0,752	0,755	0,759	0,762	0,765	0,769
0,78	0,772	0,776	0,779	0,782	0,786	0,789	0,793	0,796	0,800	0,803
0,79	0,806	0,810	0,813	0,817	0,820	0,824	0,827	0,831	0,834	0,838

Окончание табл. П.2

0,80	0,842	0,845	0,849	0,852	0,856	0,860	0,863	0,867	0,871	0,874
0,81	0,878	0,882	0,885	0,889	0,893	0,896	0,900	0,904	0,908	0,912
0,82	0,915	0,919	0,923	0,927	0,931	0,935	0,938	0,942	0,946	0,950
0,83	0,954	0,958	0,962	0,966	0,970	0,974	0,978	0,982	0,986	0,990
0,84	0,994	0,999	1,003	1,007	1,011	1,015	1,019	1,024	1,028	1,032
0,85	1,036	1,041	1,045	1,049	1,054	1,058	1,063	1,067	1,071