Метод покоординатной оптимизации

Процесс поиска оптимума методом покоординатной оптимизации в гра­фическом виде для двумерного случая представлен на рис.6.6. По этому мето­ду выбирается произвольная точка М₀ и определяются ее координаты. Поиск оптимума осуществляется поочередным варьированием каждого их факторов. При этом сначала изменяют один фактор (xi) при фиксированных остальных (x₂=const) до тех пор, пока не прекращается прирост функции отклика (точка

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

МО. В дальнейшем изменяется другой фактор (х₂) при фиксированных осталь­ных (xi=const), и далее процедура повторяется.

Вз В4 В5

Вб Вб>В5>В4

Данный метод весьма
прост, однако при большом чис­
ле факторов требуется значи­
тельное число опытов, чтобы
достичь координат оптимума.
Более того, при некото-

Рис.6.6. К методу покоординатной оптимизации

рых зависимостях y=f(xi,...,x_k) этот метод может привести к ложному результату. На рис.6.6 показан один из таких частных случаев, когда поочередное из­менение каждого из факторов в любую сторону вдоль коорди-

натных осей xi и х₂ вызывает уменьшение у. В результате решения находится ложный экстремум, находящийся в точке А' с координатами 5q;x 2 , в то время

как действительное значение максимума у_тах находится в точке А с координа­тами Xi* и х₂*.

В дальнейшем рассмотрим более совершенные методы.

Метод крутого восхождения

Известно, что кратчайший, наиболее короткий путь — это движение по градиенту, т.е. перпендикулярно линиям равного уровня, на которых функция отклика принимает постоянные значения y(xi, х₂, ..., х_к)=В. В связи с этим при оптимизации процесса рабочее движение целесообразно совершать в направ­лении наиболее быстрого возрастания функции отклика, т.е. в направлении градиента функции у.

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

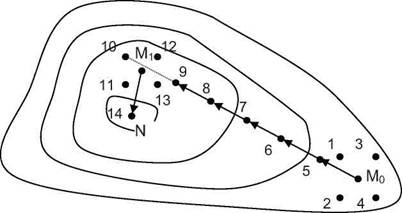
Существуют различные модификации градиентного метода, одним из них является метод крутого восхождения. Сущность этого метода также рассмот­рим на примере двухфакторной задачи (рис.6.7).

¹---------------------------------------------------------------------------------------------------------------- ►

X]

Рис. 6.7. Процедура оптимизации методом крутого восхождения

В этом случае шаговое движение осуществляется в направлении наиско­рейшего возрастания функции отклика, т.е. grad y(xi,x₂). Однако направление корректируют не после каждого следующего шага, а при достижении в некото­рой точке на данном направлении частного экстремума функции отклика.

Пусть в окрестности точки М₀ как центра плана поставлен ПФЭ 2². Коор­динаты отдельных опытов соответствуют точкам 1-4. По результатам ПФЭ можно рассчитать коэффициенты линейного уравнения регрессии.

y = bo+b 1 x 1+b 2 x 2 .

Градиент функции отклика в этой точке определяется как

ду г ду -г
grad у =-1+•], (6.37)

дх\ дх2

где i, j — единичные векторы в направлении координатных осей.

Следовательно, для движения по градиенту необходимо изменять фак­торы пропорционально их коэффициентам регрессии и в сторону, соответст­вующую знаку коэффициента. В процессе поиска двигаются в этом направле-

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

нии до тех пор, пока не будет обнаружен локальный максимум (точка М_: на рис. 6.7). В точке последнего находят новое направление градиента (направление М-iN), осуществляя опять же ПФЭ, и далее процедура повторяется. Стрелками на рис. 6.7 показана траектория движения к оптимуму.

Практически алгоритм сводится к следующей последовательности опе­раций.

1. Планирование и постановка ПФЭ (или ДФЭ) в окрестности точки на­чального состояния хю. Расчет коэффициентов bi линейной математической модели с целью определения направления градиента.

2. Расчет произведений ЬДх, где Ах — интервалы варьирования факто­ров при ПФЭ (ДФЭ).

3. Выбор базового фактора х=х₀, у которого Ъ[Ах[ = а = max.

4. Выбор шага крутого восхождения для базового фактора h_a.

Этот выбор производится на основании имеющейся априорной инфор­мации или с учетом опыта исследователя, технологических соображений или других критериев. Относительно выбора шага заметим, что слишком малый шаг потребует значительного числа опытов при движении к оптимуму, а большой шаг создает опасность проскакивания области оптимума.

5. Расчет шагов изменения других факторов по формуле

h i = (t>iAx i ) h a /а. (6.38)

Это соотношение между величинами шагов изменения отдельных факто­ров обеспечивает движение по градиенту в факторном пространстве.

6. Составление плана движения по градиенту. Для этого в соответствии с
определенными значениями шагов изменения факторов и их последователь­
ным алгебраическим суммированием с основным уровнем в точке

x ik ⁼ x i0 + kh{, k = 1,2,...

находят координаты опытов 5, 6, 7, 8, 9, 10 (см.рис.6.7). Часть этих опытов по­лагают "мысленными". "Мысленный" опыт заключается в получении предска­занных (расчетных) значений функции отклика по линейному уравнению рег-

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

рессии, что позволяет сократить объем реальных опытов, т.е. увеличить ско­рость продвижения к экстремуму. При "мысленном эксперименте" перевод ко­ординат в кодированную форму и подстановка их в уравнение модели объекта должна подтвердить действительное возрастание у. Обычно реальные опыты в начале движения из базовой точки вдоль направления градиента ставятся че­рез 2-4 мысленных опыта. Другие опыты реализуют на практике, определяя по­следовательность значений у в направлении градиента. Из опытных данных находят положение локального экстремума (точка Mi на рис.6.7).

7. В окрестности локального экстремума ставят новую серию опытов (ПФЭ или ДФЭ) для определения новых значений коэффициентов уравнения регрессии и нового направления градиента (направление М-iN на рис.6.7). В дальнейшем процедура повторяется до достижения следующего локального экстремума и так далее вплоть до определения окрестности координат макси­мума функции отклика, которая носит название почти стационарной области.

Признаком достижения этой области является статистическая незначи­мость коэффициентов Ь. В почти стационарной области становятся значимы эффекты взаимодействия и квадратичные эффекты. Здесь требуется перехо­дить от ДФЭ (если он использовался ранее) к ПФЭ, а если и этого окажется не­достаточно, перейти от планов эксперимента первого порядка к планам второго порядка.

Очевидно, что в задачах, где требуется определить координаты не мак­симума, а минимума функции отклика, знаки коэффициентов Ь\ следует поме­нять на обратные. В этом случае движение в факторном пространстве осуще­ствляется по направлению, противоположному вектору градиента.

6.5.3. Симплексный метод планирования

Метод симплексного планирования позволяет без предварительного изу­чения влияния факторов найти область оптимума. В этом методе не требуется вычисления градиента функции отклика, поэтому он относится к безградиент­ным методам поиска оптимума. Для этого используется специальный план экс­перимента в виде симплекса.

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

Симплекс — это простейший выпуклый многогранник, образованный к+1 вершинами в k-мерном пространстве, которые соединены между собой прямы­ми линиями. При этом координаты вершин симплекса являются значениями факторов в отдельных опытах. Так, например, в двухфакторном пространстве (на плоскости) к=2 симплекс — любой треугольник, в трехфакторном (трехмер­ном) к=3 пространстве — тетраэдр и т.д.

Симплекс называется правильным или регулярным, если все расстояния между образующими его вершинами равны (равносторонний треугольник, пра­вильный тетраэдр и др.).

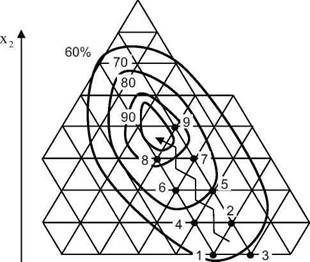
После построения исходного симплекса и проведения опытов при значе­ниях факторов, соответствующих координатам его вершин, анализируют ре­зультаты и выбирают вершину симплекса, в которой получено наименьшее (наихудшее) значение функции отклика. Для движения к оптимуму необходимо поставить опыт в новой точке, являющейся зеркальным отображением точки с наихудшим (минимальным) результатом относительно противоположной грани симплекса. На рис.6.8 представлено геометрическое изображение симплекс-метода для двумерного случая к=2.

¹---------------------------------------------------------------------- ►

X,

Рис. 6.8. Схема движения к оптимальной области симплексным методом

По итогам проведения опытов 1, 2 и 3 худшим оказался опыт 3. Следую­щий опыт ставится в точке 4, которая образует с точками 1 и 2 новый правиль-

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

ный симплекс. Далее сопоставляются результаты опытов 1, 2 и 4. Наихудший результат получен в точке 1, поэтому она в новом симплексе заменяется зер­кальным отображением (точкой 5) и т.д., пока не будет достигнута почти ста­ционарная область. Следует заметить, что хотя этот путь и зигзагообразен, общее число опытов, необходимых для достижения области оптимума, может быть небольшим за счет того, что проводить к+1 опыт приходится лишь в нача­ле, а в дальнейшем каждый шаг сопровождается проведением только одного дополнительного опыта, условия которого выбираются на основе предшест­вующих результатов.

После изложения основных идей симплексного метода планирования оп­тимальных экспериментов остановимся на некоторых его деталях. Выбор раз­меров симплекса и его начального положения в известной степени произволен. Для построения начального симплекса значения в каждом опыте исходного симплекса определяются по формуле

x ii ⁼ x i0 + QiAx i , (6.39)

где хо — координаты центра начального симплекса; Ах — интервал варьирова­ния i-ro фактора; Су — кодированное значение i-ro фактора для j-ro опыта, вы­бираемые из числовой матрицы для симплексного планирования, приведенные в табл. 6.18.

Таблица 6.18
___________ Коэффициенты Сд для выбора координат симплекса *

Номер опыта (1 \)	Факторы (-> i)
Х1	X2	Хз		Хк-1	Хк
1 2 3 4 кк+1	ki	кг	кз		Кк-1	Кк
-Ri					Кк
	-Рч2				Кк
		-R3			Кк
					Кк
				R k-i	Кк
					Rk

), 1 /+1 1 „ /
К=------ л----- ⁼J----------- ' ^i⁼i------------ ' i = 1,2,...,к,

/ +1 V2/ \ 2i(i +1) \ 2(/ +1)

где к - число факторов

Если, например, необходимо составить симплекс-план для двух факто­ров, то вначале ставят три опыта со следующими координатами:

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

1-Й ОПЫТ

xn = xio + ki^Axi;

^х21=^х20+^к2^Ах2'

2-й опыт

x 12=x 10-R 1Ax 1 ; ^х22=^х20+^к2^Ах2'

3-й опыт

^х13 ^{= х}10 ⁺ О'

x 23=x 20"R 2^Ax 2'

Симплекс, рассчитанный по этим формулам, представлен на рис.6.9.

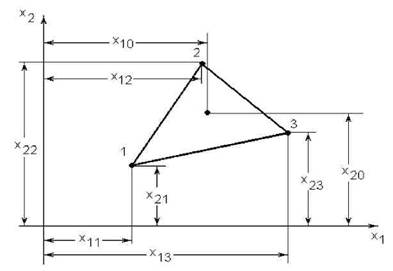
Рис. 6.9. Схема построения начального симплекса

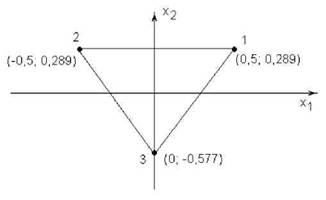
Так, если x₁₀=0 и x₂0=0, a Ax1=Ax₂=1, то координаты опытов будут равны (см. рис.6.10): опыт 1 (0,5;0,289), опыт 2 (-0,5; 0,289) и опыт 3 (0;-0,577), что со-ответствует координатам вершин равностороннего треугольника с длиной сто-роны, равной 1. Начало координат в этом случае находится в точке пересече­ния медиан (биссектрис).

Для определения условий проведения опыта в отраженной точке (коор-динат новой вершины симплекса) используется формула

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

2Й
^хы = Zj^xu ~^хь' i*^l3> (6.40)

где x_iн — координата новой точки (новой вершины) симплекса для i-й перемен­ной; x_iз — координата заменяемой точки (координата вершины симплекса с

1 ^

наихудшим откликом перед ее отбрасыванием); 2_,х_1} — среднее значение из

координат всех вершин симплекса, кроме заменяемой.

Известны следующие критерии окончания процесса последовательного отражения наихудших вершин и постановки очередных опытов в новых верши­нах:

1. Разность значений
функции отклика в вершинах
симплекса становится меньше
ранее заданной величины. Это
означает либо выход в "почти
стационарную" область вблизи
оптимума, либо достижение
участка поверхности

Рис.6.10. Координаты вершин симплекса y = f(x₁;...;x_k) = const в виде "пла-

при x_i0=0, Аx_i=1 и n=2

то". В этом случае дополни­тельными опытами в стороне от симплекса следует удостовериться в отсутст-вии других участков с более существенной кривизной поверхности y = f(x_l;...;x_k) и принять величину с экстремальным значением функции откли­ка за точку оптимума.

2. Отражение любой из вершин симплекса после однократного качания приводит к его возврату в прежнее положение. При этом есть основания утвер-ждать "накрытие" симплексом точки оптимума.

3. Циклическое движение симплекса вокруг одной из его вершин на про­тяжении более чем нескольких шагов. Подобная ситуация имеет место, когда искомый оптимум располагается внутри области, охватываемой циркулирую­щим симплексом.

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

В случаях 2 и 3 рекомендуется уменьшить размеры симплекса, т.е. рас­стояния между вершинами, и продолжить поиск до желаемого уточнения коор­динат искомого оптимума.

Изложенный алгоритм симплексного метода сравнительно прост, он дос­таточно эффективен, однако работает недостаточно быстро. Существует его модификация, известная под названием "метод деформируемого симплекса", которая ускоряет процесс поиска оптимума за счет использования на данном шаге информации, накопленной на предыдущих шагах.

к+\

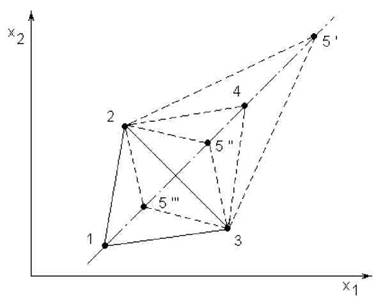
Сущность метода поиска по деформированному симплексу заключается в том, что при отражении наихудшей вершины относительно центра тяжести противоположной грани размер симплекса не остается постоянным, а осущест­вляется его деформация (растяжение или сжатие). Для пояснения существа метода введем координату центра тяжести х[ остальных (за исключением наи­худшей) вершин симплекса:

х_{ = V х.. /к; ]ф /₃. Тогда формула (6.40) может быть преобразована к виду

x iH=2x i"x i3

или xj_H = х{ + а(х{ - х^₃)•

При а=1 получим выражение (6.40) и 5q_H =xj_H.

Введем обозначения:

Уз — наихудший (минимальный) отклик в симплексе;

Утах — наилучший (максимальный) отклик;

Уз’ — отклик, следующий за наихудшим.

Следовательно у₃ < у_тах < Уз'.

В зависимости от значения функции отклика в точке нормального отра­жения у_н при а=1 возможны следующие варианты:

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

1) если уз < у_н < Утах, т.е. х_н будет нехудшей и нелучшей точкой в новом наборе точек, то x_i3 следует заменить на x_iH с а=1. В этом случае осуществляет­ся нормальное отражение;

2) если у_н > y_max, то x_iH оказывается новой лучшей точкой в новом наборе точек. В этом случае направление растяжения признается “весьма удачным” и симплекс растягивается в нормальном направлении. Для этого случая 1<а<2 и а называется коэффициентом растяжения;

3) если у₃ < у_н < Уз’, то направление отражения признается правильным, но симплекс слишком велик и его следует сжать выбором коэффициента сжа­тия а из диапазона 0<а<1;

4) если у_н < Уз, то даже направление отражения выбрано неверно и сле­дует осуществить отрицательное сжатие выбором отрицательного значения ко­эффициента а (-1<а<0).

Таким образом, на каждом шаге следует вна­чале нормально отразить наихудшую вершину сим­плекса (а=1), поставить в этой точке опыт, опреде­лить у_н, а затем поставить следующий опыт в точке факторного пространства х_н, координаты которой определяются по формуле

(6.40) с учетом рассмот-

Рис.6.11. К методу деформированного симплекса ренных вариантов 1-4.

На рис.6.11 показаны точка 4 очередного опыта при нормальном отраже­нии (а=1) наихудшей вершины 1, точки 5’, 5", 5’" последующих опытов для слу­чаев соответственно растяжения (а=2), сжатия (а=0,5) и отрицательного сжатия (а=-0,5) симплекса.

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

Таким образом, метод поиска по деформированному симплексу обладает повышенной гибкостью, позволяющей учитывать особенности поверхности от­клика.

Пример 6.1[18]. Пусть объект обладает свойствами, соответствующими уравнению

у = 4 + 12xj -х² +30х₂ -3x2.

Найдем экстремум функции симплекс-методом. Выберем основной уро­вень факторов. Предположим, что по некоторым данным экстремум находится вблизи значений xi ₀=3 и х₂ о= -1, которые и принимаем за основной уровень. Интервал варьирования примем равным Axi=1 и Ах₂=1,5. Найдем

0,5;

1 „ 0,5; к

ki =

--------- 7------- \ — ^U?^J5 ^гч-1 — _л -------- 7------- \

2 • 1 • (1 +1) \ 2 • (1 +1)

2 —7---- г = 0,577. 2 • (2 +1)

К =

1 _п __ЛЛ _,

2-2-(2 + l)⁼ \

Находим координаты первых трех опытов, так как т+1=2+1=3.

Вершина 1: х-и = 3+0,5-1=3,5; х₂1 = -1+0,289-1,5= -0,565;

Вершина 2: xi₂ = 3-0,5-1=2,5; х₂₂ = -1+0,289-1,5= -0,565;

Вершина 3: х-|з = 3+0=3; х₂з = -1-0,577-1,5= -1,865.

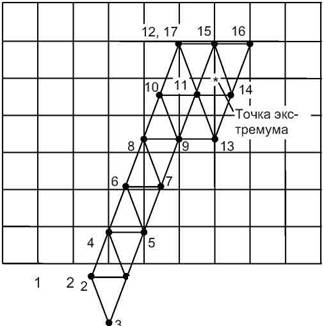
Подставляя найденные координаты вершин в уравнение, получили сле­дующие результаты опыта: у₁=15,84; у₂=9,78; у₃= -35,5. Самый худший резуль­тат у₃= -35,5. Следовательно, условия опыта 3 следует заменить. Геометриче­ская траектория движения показана на рис. 6.12.

Вычисляем координаты вершины 4.

2(3,5 + 2,5) „ 2(-0,565-0,565) г,

х₁₄ =----------- -3 = 3; х₂₄=----------------------- + 1,865 = 0,735. Результат - у4=52,1.

2 2

Сравнивая результаты y-i, у₂ и у₄, видим, что худший результат у₂. Вы­числяем координаты вершины 5:

x-i5 = 4; х₂5 = 0,735; ys= 57,1.

Вычисляем координаты вершины 6, заменяя вершину 1:

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

х-|б= 3,5; х₂б= 2,035;

Уб= 82,6.

Далее получим вершины 7 с координатами (4,5;2,035); 8 (4;3,3); 9 (5;3,3); 10 (4,5;4,8); 11 (5,5;4,8) и результаты последних трех опытов:

уэ= 105; ую= 113; уц = 112,32.

Находим координаты вершины 12:

2(4,5 +5,5)

5 =5; х

2(4,6 +4,б)

3,3 =5,9;

У12 = 111-

Как видно, координаты вершины 12 соответствуют худшим результатам, чем 10 и 11. Поэтому возвращаемся к предыдущему симплексу с вершинами 9,10, 11 и выбираем худший результат, не обращая внимания на опыт 9. Следовательно, заменить необходимо вершину 10:

1 4 5 6 7 8 xi

Х2 6

5 4 3 2

Рис. 6.12.К решению примера 6.1

^хш =

2(5 +5,5)

-4,5 =6; х

2(5,3 -4,6)

-4,6 =3,3;

у-1з= 106.

В новом симплексе 9 (5;3,3); 10 (5,5;4,6) и 13 (6;3,3) худший результат у опыта 9. Заменим вершину 9:

2(5,5 + б)

-5 =6,5; х

2(4,6 +3,3)

-3,3 = 4,6; у-и= 114,21.

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

Результаты опытов 11, 13 и 14 следующие: уц = 112,32, yi3 = 106 и Уи=114,21. Заменим вершину 13:

2(5,5 +6,5) ^ 2(4,6 +4,6)
х₁₁₅ =------------- -6 =6; х₂₁₅ =------------------3,3 =5,9;у-|5 = 112.

2 2

Получен худший результат, чем в опытах 11 и 14. Поэтому заменяем опыт 11:

2(б,5 + б)2(4,6 +5,9)
х₁₁₆ =------------5,5 =7; х₂₁₆ —^--------------4,6 =5,9; у16 = 111.

2 2

Это также худший результат, поэтому в симплексе 11, 14 и 15 заменяем опыт 14:

2(5,5 +б)2(4,6 +5,9)

х₁₁₇ =------------ -6,5 =5; х₂₁₇ =-------------- -4,6 =5,9.

2 2

Вершины 17 и 12 совпадают, у₁₇ = yi₂ = 111. Получен снова худший ре­зультат. Следовательно, экстремум находится внутри этого симплекса (см. рис. 6.12). Далее можно уменьшить интервал варьирования и от любой вершины двигаться вновь. Если же с точностью до шага варьирования результаты уст­раивают, можно считать задачу решенной.

Следовательно, координаты экстремума

xi«6,5 и х₂«4,6; у=114,21.

Истинные координаты экстремума

xi=6 и х₂=5; у=115.

Контрольные вопросы

1. Из каких этапов состоит последовательность проведения активного экспе­римента?

2. С какой целью используют теорию планирования эксперимента?

3. Из каких соображений выбирают основные факторы, их уровни, а также ин­тервалы варьирования факторов при проведении ПФЭ и ДФЭ?

4. В чем заключается основная идея ДФЭ?

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

5. В чем заключаются причины неадекватности математической модели? Как производится оценка адекватности?

6. Каковы принципы ротатабельного планирования эксперимента?

7. С какой целью композиционные планы приводят к ортогональному виду?

8. В чем заключается сущность планирования экспериментов при поиске опти­мальных условий? Какие методы при этом используют?

9. На чем основан метод покоординатной оптимизации?

10. Из каких этапов состоит алгоритм оптимизации методом крутого восхожде-ния?

11. В чем заключаются основная идея метода симплексного планирования?