Разработка математической модели гидравлического режима методической печи

В качестве примера рассмотрим разработку математической модели гидравлического режима четырехзонной методической печи с использованием теории планирования эксперимента. При планировании опытов используем ме­тодику проведения дробного факторного эксперимента (ДФЭ) первого порядка с двухуровневым варьированием факторов.

Перед разработкой плана эксперимента на основе априорной информа­ции были выявлены факторы, влияющие на величину давления в томильной зоне печи. К числу таких факторов относятся расходы топлива на каждую зону нагрева и угол поворота дымового клапана. Расходы воздуха на каждую зону в

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

качестве факторов не фигурировали, поскольку схема управления горением то­плива автоматически меняет расход воздуха при изменении расхода газа.

Обозначим факторы: X, — расход газа в томильной зоне, м³/ч; Х₂ — рас­ход газа во второй сварочной зоне, м³/ч; Х₃ — расход газа в первой сварочной зоне, м³/ч; Хд — расход газа в нижней сварочной зоне, м³/ч; Х₅ — положение дымового клапана, % хода исполнительного механизма (рис.6.2).

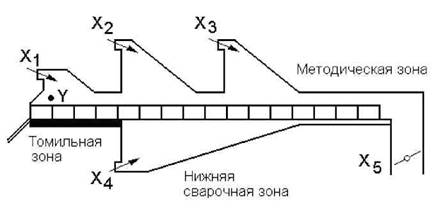
Рис.6.2. Положение факторов (Х_ь ..., Х₅) и отклика (Y) при проведении исследования на методической печи

Реализация ПФЭ в этом случае при варьировании всех факторов на двух уровнях потребовала бы постановки 2⁵=32 опытов.

Будем предполагать, что эффекты взаимодействия факторов в иссле­дуемом объекте маловероятны и пренебрежимо малы. Воспользуемся 1/4 реп­ликой ПФЭ, т.е. ДФЭ типа 2⁵"², где формально 2 фактора заменены соответст­вующими произведениями остальных факторов (X4=xi х₂, x₅=xi х₂ Хз). Это позво­лит сократить число опытов до 2³=8. Уровни варьирования факторов представ­лены в табл. 6.6.

Таблица 6.6 Уровни варьирования факторов

Уровни факторов	Факторы
X-i, м3/ч	х2, м3/ч	Хз, м3/ч	Хд, м3/ч	Хб, % хода ИМ
Основной (нулевой)
Нижний
Верхний
Интервал варьирования

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

В табл. 6.7 приведены матрица планирования ДФЭ 2⁵"² и результаты экс­перимента — значения выходной переменной (давления в томильной зоне ме­тодической печи).

Для обработки результатов эксперимента используем методику, изло­женную ранее в параграфе 4.5.

1. Расчет построчных средних:

y jl+y j 2+- + y j m*

У i =------------------------------------------------- j

J m*

где m* — число повторных опытов (m*=2). Например,

(-2,6) + (-2,5)

-2,55.

Результаты расчета представлены в табл. 6.7.

Таблица 6.7 Матрица ДФЭ 2⁵-² с двумя параллельными опытами

	Переменная состояния (отклик), кПа	Построчная дисперсия щ
	Опы т 1	Опы т 2	Сред­нее	Мо­дель
Хо	Xi	х2	Хз	Хд	Хб	У1	Y2	у.	Уi
						-2,5	-2,6	-2,55	-2,41	0,005
	-1			-1	-1	2,2	2,3	2,25	2,26	0,005
		-1		-1	-1	5,1	4,7	4,90	4,74	0,080
	-1	-1				-1,1	0,5	-0,30	0,08	1,280
			-1		-1	2,1	2,3	2,20	2,26	0,020
	-1		-1	-1		-2,0	-2,4	-2,20	-2,41	0,080
		-1	-1	-1		0,0	0,8	0,40	0,08	0,320
	-1	-1	-1		-1	4,2	5,1	4,65	4,74	0,405

2. Определение построчных (выборочных) дисперсий:

s2 =

т* -\

', S₁

(-2,5 - (-2,55))² + (-2,6 - (-2,55))" 2-1

0,005.

Аналогично S₂²=0,005; Бз²=0,08; S4²=1,28; Ss²=0,02; S6²=0,08; S7²=0,32; S₈²=0,405. Сумма построчных (выборочных) дисперсий:

Se²=0,005+0,005+0,08+1,28+0,02+0,08+0,32+0,405=2,195.

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

3. Определение однородности дисперсий по критерию Кохрена:

_Symax 1,28

и_жсй =^ =---------------- =0,5831.

Sj.2,195

Далее по табл. П.9 находим G_a;m;n. Для a=0,05, m=m*-1=2-1 и n=8 значе­ние G0,05;1;8=0,6798. Поскольку G_3KCn< G_Teo_P, то дисперсии однородны.

4. Определение коэффициентов в уравнении регрессии:

п __

y=i -2,55 +2,25 +4,9 -0,3 +2,2 -2,2 +0,4 +4,65

о₀ =------------------- =----------------------------------------------------------------------------- =1,169;

п 8

у \ у • х_х.

1 ы ^J -2,55-2,25 +4,9 +0,3 +2,2 +2,2 +0,4-4,65

Ь_х--------------------- =------------------------------------------------------------------------------ =0,069;

п 8

п __

/,у, ■ х₂

2,55 +2,25 -4,9 +0,3 +2,2 -2,2 -0,4 -4,65

Ь₂---------------------- =------------------------------------------------------------------------------ =-1,244;

п 8

п __

Z

V ■ ' X, ,

1 /=i-2,55 +2,25 +4,9-0,3-2,2 +2,2-0,4-4,65

о₃ =------------------ =---------------------------------------------------------------------------- =-0,094;

п 8

п __

2_,у j' x₄j

1=1 -2,55-2,25-4,9-0,3 +2,2 +2,2-0,4 +4,65

b₄ =------------------ =---------------------------------------------------------------------------- =-0,169;

п 8

п __

У^_у. •x_5j

, ;=\ -2,55-2,25-4,9-0,3-2,2-2,2 + 0,4-4,65

о₅ =----------- =-------------------------------------------------- = -2,331.

п 8

5. Проверка значимости коэффициентов регрессии. Предварительно оп­ределим дисперсию воспроизводимости (дисперсию отклика):

о2 i=i ^s2,195 Ь --------- = =----------- =0,2744.

Z

C2 j 1

n п 8

Дисперсия коэффициентов уравнения регрессии

2 SBn(,n 0,2744 £7Г Sb =-------- =--------- = 0,01715; Sb = JSb = 0,131.

2 во

n-m* 8-2

Находим значение доверительного интервала для коэффициентов рег-рессии:

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

^Ab j⁼ta;m-S b-

Здесь m=n(m*-1)=8(2-1)=8, тогда теоретическое значение критерия Стью-дента t₀,05;8=2,31 (можно рассчитать, используя функцию электронных таблиц Microsoft Excel СТЬЮДРАСПОБР(0,05;8)=2,31), откуда ЛЬр2,310,131=0,303. Из сопоставления доверительного интервала Abj с абсолютными значениями ко­эффициентов модели следует, что I bi | =0,069<0,303; | Ьз I =0,094<0,303 и I Ь>41 =0,1690,303. Эти коэффициенты оказались незначимы, а остальные зна­чимы. Таким образом, окончательное уравнение регрессии запишется в виде

у =1,169-1,244Х₂-2,331Х₅.

Результаты расчета выходных параметров по уравнению полученной модели у[ занесены в табл. 6.7.

6. Проверка адекватности полученной модели. Предварительно опреде­лим дисперсию адекватности:

I I

= ад

si

п-1 В нашем случае т*=2; /7=8; 1=3, и в результате имеем

5ад =---- 1(—2,55 + 2,41)² + (2,25 - 2,66)² + (4,9 - 4,74)² + (-0,3 - 0,08)

8-3

+ (2,2-2,26)² +(-2,2 + 2,41)² +(0,4-0,08)² +(4,65-4,74)²] = 0,1386.

С учетом ранее найденной выборочной дисперсии Sz²=2,195 определяем дис­персию воспроизводимости:

г.2 S_y 2,195

S_B0Cn = — =-------------- = 0,274.

n 8

Экспериментальное значение критерия Фишера следующее:

,_, S 0,1386

F_3KCII = =------------- = 0,505.

^вош 0,2744

Теоретическое значение критерия Фишера F_am1m2 при а=0,05 можно опреде­лить по справочнику [11], табл. П.4 или с помощью встроенной функции элек-

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

тронных таблиц Microsoft Excel FPACnOBP. Для m₁=(n-l)=(8-3)=5 и m₂=n(m*-1)=8(2-1)=8 значение Fo,o5;5;8=3,69 (FPACnOBP(0,05;5;8)=3,69). Поскольку F_3Kcn< F_Teop, то полученная модель адекватна.

Планы второго порядка

Описание поверхности отклика полиномами первого порядка часто ока­зывается недостаточным. Во многих случаях удовлетворительная аппроксима­ция может быть достигнута, если воспользоваться полиномом второго порядка (6.7).

В этом случае требуется, чтобы каждый фактор варьировался не менее чем на трех уровнях. В этом случае полный факторный эксперимент содержит слишком большое количество опытов, равное З^к. Так, при к=3 их 27, а число ко­эффициентов b - 10, при к=5 число опытов 243, а коэффициентов 21. В связи с этим осуществление ПФЭ для планов второго порядка не только сложно, но и нецелесообразно.

Сократить число опытов можно, воспользовавшись так называемым ком­позиционным или последовательным планом, разработанным Боксом и Уилсо-ном. Так, при двух факторах модель функции отклика у = f(xi,x₂) второго поряд­ка представляет собой поверхность в виде цилиндра, конуса, эллипса и т.д., описываемую в общем виде уравнением

У - Ь₀ + Ь₁Х₁ + Ь₂Х₂ +Ь₁₁ JC₁ +Ь₂₂Х₂ +h₁₂^X₁^X2 .

Для определения такой поверхности необходимо располагать координа­тами не менее трех ее точек, т.е. факторы x-i и х₂ должны варьироваться не ме­нее чем на трех уровнях. Поэтому план эксперимента в плоскости факторов xi и х₂ на рис.6.3, а не может состоять лишь из опытов 1, 2, 3, 4 ПФЭ 2², распола­гающихся в вершинах квадрата, как это было для модели первого порядка. К ним должны быть добавлены опыты (звездные точки) 5, 6, 7, 8, расположенные на осях xi и х₂ с координатами (±а;0), (0;±а) и обязательно опыт 9 в центре квадрата, чтобы по любому направлению (5-9-6), (1-9-4) и т.д. располагалось три точки, определяющие кривизну поверхности в этом направлении.

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

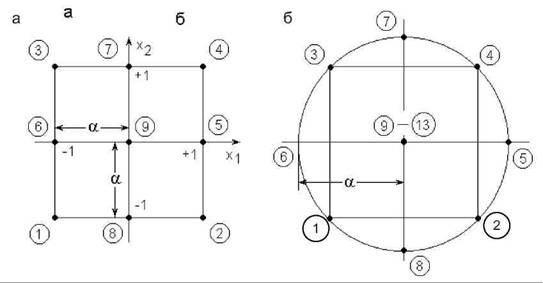Рис. 6.3. Планы второго порядка при k=2: а — ортогональный; б — ротатабельный

Таким образом, в общем случае ядро композиционного плана составляет при к<5 ПФЭ 2^к, а при к>5 — дробную реплику от него. Если линейное уравне­ние регрессии оказалось неадекватным, необходимо:

1) добавить 2к звездных точек, расположенных на координатных осях факторного пространства (±а,0,0,...,0), (0,±а,0,...,0), ..., (0,0,...,±а), где а — звездное плечо, или расстояние до звездной точки;

2) провести п₀ опытов при значениях факторов в центре плана.

При к факторах общее число опытов в матрице композиционного плана составит

n=2^k + 2k +По при к<5,

п=2^к"¹ + 2к +По при к>5.

При этом величина звездного плеча а и число опытов в центре плана п₀ зависит от выбранного вида композиционного плана.

Композиционный план для к=2 и п₀=1 представлен в табл.6.8.

Таблица 6.8

Композиционный план второго порядка

Номер

Факторы

Результат

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

опыта	Хо	Х1	х2	XiX2	х-i2	х22	У\
Ядро 2 плана 3	+1 +1 +1 +1 +1	-1 +1 -1 +1 +а	-1 -1 + 1 +1 0	+1 -1 -1 +1 0	+1 +1 +1 +1 а2	+1 +1 +1 +1 0	У1 У2 Уз У4 у5
Звезд- 6 ные 7 точки 8	+1 +1 +1	-а 0 0	+а -а	0 0 0	а2	а2 а2	Уб У7 У8
Центр 9 плана	+1						у9

Аналогичным образом составляются планы и для большего числа фак-

торов.

6.4.1.Ортогональные планы второго порядка

В общем виде план, представленный в табл.6.8, неортогонален, так как

пп

^х₀₁х~² ф 0; ^х²х_и² ф0, [Фи. (6.26)

/=1

у=1

Приведем его к ортогональному виду, для чего введем новые перемен­ные (преобразования для квадратичных эффектов):

X_tJ = X_;j

/\

2 7-1

п

2

i j

2 2

При этом ^Xq-Xj- ='^₁(х_!] -Xi ) = ^S^_Jx_i] -HXi = 0.

7=1 j-\j-\

Тогда уравнение регрессии будет записано как

Композиционные планы легко привести к ортогональным, выбирая звезд­ное плечо а. В табл. 6.9 приведено значение а для различного числа факторов к и числа опытов в центре плана п₀.

Таблица 6.9

Значения звездных плеч в ортогональных планах второго порядка

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

Число опытов в центре плана По	Звездное плечо а при различном числе факторов к
к=2	к=3	к=4	к=5 *
	1,000	1,215	1,414	1,546
	1,077	1,285	1,471	1,606
	1,148	1,353	1,546	1,664
	1,214	1,414	1,606	1,718
	1,267	1,471	1,664	1,772
	1,320	1,525	1,718	1,819
	1,369	1,575	1,772	1,868
	1,414	1,623	1,819	1,913
	1,454	1,668	1,868	1,957
	1,498	1,711	1,913	2,000

** В ядре полуреплики

В частности, ортогональный план второго порядка для к=2 и п₀=1 пред­ставлен в табл. 6.10, а его геометрическая интерпретация - на рис. 6.3, а.

Представленный на рис.6.3, айв табл. 6.10 прямоугольный (квадратный) план эксперимента для модели второго порядка работоспособен, хотя и не­сколько избыточен (9 опытов для определения 6 коэффициентов). Благодаря трем избыточным опытам, он позволяет усреднить случайные погрешности и оценить их характер.

Таблица 6.10 Ортогональный план второго порядка

Номер опыта	Факторы	Резуль­тату
Хо	Х1	х2	XiX2	Xi	х2’
1 Ядро 2 плана 3	+1 +1 +1 +1	-1 +1 -1 +1	-1 -1 +1 +1	+1 -1 -1 +1	+1/3 +1/3 +1/3 +1/3	+1/3 +1/3 +1/3 +1/3	У1 У2 Уз У4
5 Звезд- 6 Ные 7 точки 8	+1 +1 +1 +1	а=+1 а=-1	0 а=+1 а=-1	0 0 0 0	+1/3 +1/3 -2/3 -2/3	-2/3 -2/3 +1/3 +1/3	У5 Уб У7 У8
Центр 9 плана	+1				-2/3	-2/3	Уэ

В этой таблице х\. = х_;/

у-1

9

= х

2

В силу ортогональности матрицы планирования все коэффициенты

I] J IJ UJ J /=1 /=1 ill п

7 /=1 о. — ' п

Z(v,.)2

7=1

7 I /=1 7

i in 22

; о..---------------; о

и

Z*1./

X

7=1

у=1

(6.27)

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

уравнения регрессии b определяются независимо один от другого по формулам

Здесь i - номер столбца в матрице планирования; j - номер строки; суммы в знаменателях различны для линейных, квадратичных эффектов и взаимодей­ствий.

Дисперсии коэффициентов уравнения регрессии следующие:

S_bl² =S²Bocn/^ x_IJ²; S 'b^S^ocn/^V^²; S_biu² =S²Bocn/^ (x_;j.x_UJ.)². (6.28)

Следует особо отметить, что коэффициенты уравнения регрессии, полу­чаемые с помощью ортогональных планов второго порядка, определяются с разной точностью (см. уравнение (6.28)), в то время как ортогональные планы первого порядка обеспечивают одинаковую точность коэффициентов, т.е. план, представленный в табл. 6.10, являющийся ортогональным и обеспечивающий независимость определения коэффициентов Ь, не является ротатабельным.

В результате расчетов по матрице с преобразованными столбцами для квадратичных эффектов получим уравнение регрессии в виде

У = V+X^"x<" ⁺ Х^<"и^хЛ + Х^»'(^х<"² ~^х'²)- (6.29)

(=1 /,м=1 г-\

Для преобразования к обычной форме записи следует перейти от коэф­фициента bo’ к коэффициенту Ь₀, используя выражение

Ь₀ =/>₀'-^/>',.,-х,-². (6.30)

(=1

При этом дисперсия этого коэффициента рассчитывается по следующе­му соотношению:

Sb0 =Svo+2^^Хг 'Sb'u •(6.31)

(=1

В дальнейшем, зная дисперсию воспроизводимости, проверяют значи­мость коэффициентов и адекватность уравнения:

y =b₀+ Y__ib_;x_i +^ b_!ux_;x_u + ^Ь_их². (6.32)

(=1 i„u=\i-\

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

Значимость коэффициентов проверяется по критерию Стьюдента t. =z>. \/s_bi . Коэффициент значим, если ц >t_am, где m - число степеней сво­боды дисперсии воспроизводимости.

Адекватность уравнения проверяется по критерию Фишера

F ^{= s}aA/SBocn- Уравнение адекватно, если составленное таким образом F-

отношение меньше теоретического: F<F_a;mi;m2, где m-i=/7-/ - число степеней

свободы дисперсии адекватности; т₂ - число степеней свободы дисперсии воспроизводимости; / - число коэффициентов в уравнении регрессии второго порядка, равное числу сочетаний из к+2 по 2, т.е.

(к +2)(к +1)
/ =----------------. (6.32а)

6.4.2. Ротатабельные планы второго порядка

Как мы установили, план второго порядка, представленный в табл.6.10, не обладает свойством ротатабельности. Ротатабельным называют планиро­вание, для которого дисперсия отклика (выходного параметра) у , предсказан­ного уравнением регрессии, постоянна для всех точек, находящихся на равном расстоянии от центра эксперимента. Экспериментатору заранее не известно, где находится та часть поверхности отклика, которая представляет для него особый интерес, поэтому следует стремиться к тому, чтобы количество инфор­мации, содержащееся в уравнении регрессии, было одинаково для всех равно­отстоящих от центра эксперимента точек. Действительно, удаление от центра точек 5,6,7,8 в V2 =1,414 раза меньше, чем удаление точек 1, 2, 3, 4 (см. рис. 6.3, а), и, следовательно коэффициенты уравнения регрессии определяются с различной дисперсией. Бокс и Хантер предложили ротатабельные планы 2-го порядка. Для того чтобы композиционный план был ротатабельным, величину звездного плеча а выбирают из условия

к

к-\

а = 2⁴ при к<5 и а = 2⁴ при к>5 (6.326)

или в общем случае

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

k-p

а =2 ⁴ ,

где к - число факторов; р - дробность реплики (для ПФЭ р=0, для полуреплики р=1, для четвертьреплики р=2 и т.д.).

Число точек в центре плана п₀ увеличивают. В табл. 6.11 приведены зна­чения а и По для различного числа независимых факторов.

Таблица 6.11 Значения звездных плеч и числа точек в центре ротатабельных планов

Параметр плана	Значения параметров при числе независимых факторов
Ядро плана	22	23	24	2Ь	г\Ь-"\	26	/рб-1	2'	г\('-1
Звездное плечо	1,414	1,682	2,00	2,378	2,00	2,828	2,378	3,333	2,828
Число точек в центре плана п0

Поясним идею выбора значения звездного плеча а на примере матрицы ротатабельного планирования второго порядка для к=2, представленной в табл. 6.12.

Размещение точек этого плана показано на рис. 6.3,6. Для обеспечения ротатабельности точек 5, 6, 7, 8 необходимо удалить их от центра плана на

расстояние а в V2 =1,414 раз большее, чем удаление точек 1, 2, 3, 4 от осей х₂ и х-i. В результате этого все точки плана (табл. 6.12) оказываются лежащими на окружности. Учитывая существенно большее влияние на функцию отклика слу­чайной ошибки в точке 9, рекомендуется ставить в этой точке плана не один, а несколько дублирующих опытов (в данном случае опыты с 9 до 13) для усред­нения полученных результатов и для осуществления статистического анализа результатов всего эксперимента в целом.

Таблица 6.12 Ротатабельный план второго порядка

Номер опыта	Факторы	Результат У
Хо	Х1	х2	XiX2	х-i2	х22
1 Ядро 2 плана 3	+1 +1 +1 +1	-1 +1 -1 +1	-1 -1 +1 +1	+ 1 -1 -1 +1	+1 +1 +1 +1	+1 + 1 + 1 +1	У1 У2 Уз У4
Звезд- 5	+1	+1,414					У5

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

ные		+1	-1,414					Уб
точки		+1		+1,414				у7
		+1		-1,414				Ув
		+1						Уэ
Центр		+1						Ую
плана		+1						Ун
		+1						У12
		+1						У13

Учитывая специфический характер ротатабельного плана в общем виде, можно также получить формулы для расчета коэффициентов уравнения рег­рессии и их дисперсий:

A

24(k + 2K-k]:

Ь0

2A,²(k + 2)(oy)-2Xc ^(iiy)

1=1

п

A

bj=(c/n)(iy);

b;;

n

c²[(k + 2)X-k](iiy) + c²(l-X)X(iiy)-2Xc(oy)

1-1

1 c² ( \

b_;„ =(iuy);

₂ 2АЯ²(к + 2) ₂

S =-------------------- S

°Ь₀ '-'восп'

n

2 A[(k + l)A-(k-l)c² Д

----- i-------------------- i--------- /----- i

S2 ■ ВОСП ?

n

S_b

2 ^C o2

=s

b '-'восп'

(oyblXy,

(iuy) = ix,

где

yf;

x„,y,;

j=i

J=l

&y)=5>

«Ур

(Н_У)=£х_у²_У];

J-l

n

с

j=l

A

(I)

(II)

(III)

(IV)

(V)

(VI)

(VII)

(VIII)

(IX) (X)

J-l

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

пк к(п, +п„)

Х=-7-------- Г--- = / s ■ (XI)

(k + 2jnj (к + 2)гц

Здесь По- число опытов в центре плана; г\-\ - число остальных опытов. Матрица ротатабельного планирования, оказывается неортогональной,

так как

Xx0j'xu,²^0; Х^хц²'^хч²^0; i^u- (6.33)

Следовательно, если какой-либо из квадратичных эффектов оказался незначимым, то после его исключения коэффициенты уравнения регрессии не­обходимо пересчитать заново.

При использовании ротатабельных планов второго порядка дисперсию воспроизводимости можно определить по опытам в центре плана. В связи с этим при проверке адекватности уравнения регрессии, полученного по ротата-бельному плану второго порядка, поступают следующим образом.

Находят остаточную сумму квадратов

S² = ^(у,- -уj)² (6.34)

с числом степеней свободы

{к + 2)(к +1)

т_х - п — 1 - п

2 По опытам в центре плана определяют сумму квадратов воспроизводи-

мости

$2 =Х(Уо; ~Уо;)² (6.35)

с числом степеней свободы т₂ = п₀ -1.

Далее находят сумму квадратов, характеризующих неадекватность

S3² = S1² - S₂² , число степеней свободы которой

(к +2)(к + \)
т₃ =т_х-т₂ = п-------------------- (п₀ -1).

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

Проверяют адекватность по F-критерию:

So/тз
F = —^----- . (6.36)

Уравнение адекватно, если F<F_a;_m3;m2-

Если модель второго порядка оказалась неадекватной, следует повто­рить эксперименты на меньшем интервале варьирования факторов или пере­нести центр плана в другую точку факторного пространства. В тех случаях, ко­гда адекватность модели по-прежнему не достигается, рекомендуется перейти к планам третьего порядка.

6.4.3. Исследование причин образования расслоений в горячекатаных листах

В качестве примера планирования эксперимента второго порядка рас­смотрим задачу исследования причин образования расслоений в горячеката­ных листах (за основу числового материала взяты данные из книги¹ \

Известно, что при прокатке листов толщиной более 12 мм появление брака связано большей частью с дефектами, унаследованными от слитка. Наи­более серьезными дефектами толстого листа являются расслоения, трещины и рванины.

Существует достаточно тесная связь между некоторыми параметрами выплавки стали и пораженностью листов расслоениями. По результатам ульт­развуковой дефектоскопии было установлено, что на пораженность листов рас­слоениями (которая количественно может быть выражена в относительных единицах по площади расслоений, отнесенной к площади всего раската - Y, %) наиболее существенно влияют такие два фактора, как скорость выгорания уг­лерода в период рудного кипения -х-i, %/ч, и время разливки стали -х₂, мин.

Уровни варьирования факторов представлены в табл. 6.13.

Таблица 6.13

¹ Паршин В.А, Зудов Е.Г., Колмогоров В.Л. Деформируемость и качество. - М.Металлургия, 1979.

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

Уровни варьирования факторов

Уровни факторов	Факторы
X-i, %/ч	х2, мин
Основной (нулевой)	0,35	5,5
Нижний	0,20	3,5
Верхний	0,50	7,5
Интервал варьирования	0,15	2,0

Для проведения эксперимента использовался ортогональный план второ­го порядка с тремя опытами в центре плана. По табл. 6.9 при числе факторов к=2 и п₀ = 3 величина звездного плеча составляет а = 1,148«1,15, поэтому мат­рица планирования выглядит (табл.6.14) следующим образом:

Таблица 6.14

Ортогональный план второго порядка для двух факторов и с тремя опытами в центре плана

	Факторы (кодированные значения)	Факторы (натуральные значения)	Отклик
Х1	х2	X-i, %/ч	х2, мин	у, %
1 Ядро 2 плана 3	-1	-1	0,20	3,5	0,36
+1	-1	0,50	3,5	0,51
-1	+1	0,20	7,5	1,33
+1	+1	0,50	7,5	1,51
5 Звезд- 6 ные 7 точки 8	а = +1,15		0,52	5,5	0,50
а = -1,15		0,18	5,5	0,31
	а = +1,15	0,35	7,8	1,59
	а = -1,15	0,35	3,2	0,45
Центр 9 плана 10			0,35	5,5	0,30
		0,35	5,5	0,29
		0,35	5,5	0,31

Для обработки результатов эксперимента используем методику, изло­женную ранее в параграфе 6.4.1.

Начнем с того, что к кодированным значениям xi и х₂ в исходную таблицу плана (см.табл.6.14) добавим фиктивный столбец х₀=1, а также дополнитель­ные СТОЛбЦЫ Xi₂=XiX₂.

х₁ = х₁

у

/ \ Х1■

2 7-1

И

х₂ = х₂

/

/ \ х2.

2 7-1

2

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

Поскольку

11 11

2jxi7 ⁼ Sx27 ⁼ (~1)² + (+1)² + (~1)² + (+1)² + (+1Д5)² + (—1Д5)² + (О)² +... + (О)² = 6,636,

7-1 j -1

то х_Х] = х_Х]

6,636 11

2727

х_Х! - 0,6, аналогично х₂.. « х₂, -0,6.

В итоге матрица плана эксперимента с фактическими результатами экс­перимента у, полученными в ходе проведения опытов, выглядит следующим образом (табл.6.15):

Таблица 6.15 Матрица ортогонального плана второго порядка в кодированных значениях

Номер опыта	Факторы	Результат
Хо	Xi	х2	Х-|2	х-Г	х2'	У у,
1 Ядро 2 плана 3	+1 +1 +1 +1	-1 +1 -1 +1	-1 -1 +1 +1	+1 -1 -1 +1	+0,4 +0,4 +0,4 +0,4	+0,4 +0,4 +0,4 +0,4	0,36 0,366 0,51 0,526 1,33 1,346 1,51 1,506
5 Звезд- 6 ные 7 точки 8	+1 +1 +1 +1	+1,15 -1,15	0 +1,15 -1,15	0 0 0 0	+0,7225 +0,7225 -0,6 -0,6	-0,6 -0,6 +0,7225 +0,7225	0,50 0,507 0,31 0,323 1,59 1,587 0,45 0,46
Центр 9 плана 10	+1 +1 +1	0 0 0	0 0 0	0 0 0	-0,6 -0,6 -0,6	-0,6 -0,6 -0,6	0,30 0,296 0,29 0,296 0,31 0,296

В табл. 6.15 также приведены значения оценок отклика у., найденные по модели, построенной после обработки экспериментальных данных. Для оценки коэффициентов в уравнение регрессии

у = Ь₀ *+Ь_хх_х + Ь₂х₂ + Ъ_Х2х_Х2 + Ъ\_хх_хх + Ъ\₂х₂₂

по зависимостям (6.27) сформируем еще две дополнительные таблицы (табл. 6.16, 6.17), в которых представим результаты всех необходимых проме­жуточных расчетов.

Таблица 6.16

Таблица произведений кодированных значений факторов на значения отклика

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

Номер опыта	Произведения факторов на отклик
ХоУ	ХгУ	х2у	х-|2-у	x-i'y	х2'у
	0,36	-0,36	-0,36	0,36	0,144	0,144
	0,51	0,51	-0,51	-0,51	0,204	0,204
	1,33	-1,33	1,33	-1,33	0,532	0,532
	1,51	1,51	1,51	1,51	0,604	0,604
	0,5	0,575			0,36125	-0,3
	0,31	-0,3565			0,223975	-0,186
	1,59		1,8285		-0,954	1,148775
	0,45		-0,5175		-0,27	0,325125
	0,3				-0,18	-0,18
	0,29				-0,174	-0,174
	0,31				-0,186	-0,186
1-сумма	7,46	0,5485	3,281	0,03	0,305225	1,9319

Таблица 6.17 Величина квадратов кодированных значений факторов

Номер опыта	Квадраты факторов
(хо)2	(х-i)2	(х2)2	(Х12)2	(х-Г)2	(х2')2
					0,16	0,16
					0,16	0,16
					0,16	0,16
					0,16	0,16
		1,3225			0,522006	0,36
		1,3225			0,522006	0,36
			1,3225		0,36	0,522006
			1,3225		0,36	0,522006
					0,36	0,36
					0,36	0,36
					0,36	0,36
1-сумма		6,645	6,645		3,484013	3,484013

Используя значения из строк «Z-сумма» в этих двух таблицах, находим оценки коэффициентов регрессии:

Ь₀'=7,46/11 =0,678182 ;

bj =0,5485/6,645 =0,082543 ;

b₂ =3,281/6,645 =0,493755 ;

b₁₂ =0,03/4 =0,0075;

b_n'=0,305225/3,484013 =0,087607 ;

6. МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ. ЛОГИЧЕСКИЕ ОСНОВЫ

Ь₂₂'= 1,9319/3,484013 = 0,554504 .

Значимость коэффициентов проверяем по критерию Стьюдента t. = b_; |/S_b!, для чего находим дисперсию воспроизводимости S²_B0Cn по трем па­раллельным опытам в центральной точке плана:

Vi-1 /

V (у_п. - у_п) Г , ,

S_BOcn=--------------- = 2^Уо;- 2^Уо;

3-1 3-1 ~г з

((0,30)² +(0,29)² +(0,31)²)—(0,30 + 0,29 + 0,31)

0,0001

и рассчитываем по (6.28) дисперсии и средние квадратичные отклонения по каждому из коэффициентов:

S?, = 0,0001/11 = 9,09091 -10⁶; S_K, = л/9,09091-10⁶ =0,003015;

S? = S? = 0,0001/6,645 = 1,5-10"⁵; S_h =S_h = Jl,5 -10⁵ =0,003879;

S? = 0,0001/4 = 2,5-10"⁵; S. = л/2,5-10"⁵ =0,005;

S? , = S? , = 0,0001/3,484013 = 2,87-10"⁵; S_h , =S_h , = л/2,87-10~⁵ =0,005357.

11 22 "ll "22 *

Тогда критерий Стьюдента по каждому из коэффициентов составит:

t_b, = 0,678182/0,003015 = 224,9;

t_b =0,082543/0,003879 = 21,2; t_b =0,493755/0,003879 = 127,3; t, =0,0075/0,005 = 1,5;

t, , =0,087607/0,005357 = 16,3; t, ,=0,554504/0,005357 = 103,5.

Поскольку критическое значение t₀,₀5;3-i=4,30 (СТЬЮДРАСПОБР(0,05;2)= =4,302655725), то все коэффициенты в уравнении регрессии можно считать значимыми, кроме bi₂.

6. МЕТОДЫ ПЛАНИРОВАН