Определение тесноты связи между случайными величинами

Определив уравнение теоретической линии регрессии, необходимо дать количественную оценку тесноты связи между двумя рядами наблюдений. Линии регрессии, проведенные на рис. 4.1, б, в, одинаковы, однако на рис. 4.1, б точки значительно ближе (теснее) расположены к линии регрессии, чем на рис. 4.1, в.

При корреляционном анализе предполагается, что факторы и отклики носят случайный характер и подчиняются нормальному закону распределения.

Тесноту связи между случайными величинами характеризуют корреляци­онным отношением р_ху. Остановимся подробнее на физическом смысле данно­го показателя. Для этого введем новые понятия.

Остаточная дисперсия 5^_ост характеризует разброс экспериментально

наблюдаемых точек относительно линии регрессии и представляет собой пока­затель ошибки предсказания параметра у по уравнению регрессии (рис. 4.6):

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА...

s2 =f[y.-yT

у ост -, / X г i\

п -1

п-\-к

^[_у. - f {х₁,Ъ_й,Ъ₁,...,Ъ_к)\^г,

(-1

(4.9)

где /=/с+1 - число коэффициентов уравнения модели.

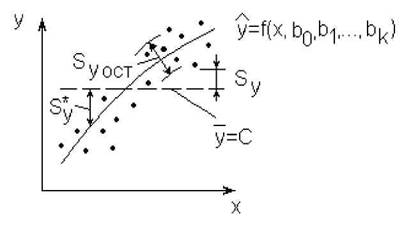Рис.4.6.К определению дисперсий

Общая дисперсия (дисперсия выходного параметра) S y характеризует

разброс экспериментально наблюдаемых точек относительно среднего значе­ния у, т.е. линии С (см. рис. 4.6):

₂ 1

!S —--------

^у п-1

2>, -у]

1=1

(4.10)

где у = !>;.

Шi-i

Средний квадрат отклонения линии регрессии от среднего значения ли­нии у = С (см. рис. 4.6):

1 а

1 а

П-1

i=l

11 /Л 11 Г)

XLy i~yJ =----- Zlj(xbbo,bi,...,b k )-yj .

i=l

П-1

(4.11)

Очевидно, что общая дисперсия S²_y (сумма квадратов относительно среднего значения у) равна остаточной дисперсии S y_0CT (сумме квадратов от­носительно линии регрессии) плюс средний квадрат отклонения линии регрес­сии S_y*² (сумма квадратов, обусловленная регрессией).

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА...

У ~ у ОСТ +^у ■

(4.11а)

Разброс экспериментально наблюдаемых точек относительно линии рег­рессии характеризуется безразмерной величиной - выборочным корреляцион­ным отношением, которое определяет долю, которую привносит величина X в общую изменчивость случайной величины Y.

* Рху

у ~ ^йу ост

'У

=

>У

Т

=

Оу S y

(4.12)

Проанализируем свойства этого показателя.

1. В том случае, когда связь является не стохастической, а функциональ­ной, корреляционное отношение равно 1, так как все точки корреляционного

поля оказываются на линии регрессии, остаточная дисперсия равна S

у ост

О,

a S y = S y (рис. 4.7, а).

2. Равенство нулю корреляционного отношения указывает на отсутствие какой-либо тесноты связи между величинами х и у для данного уравнения рег­рессии, поскольку разброс экспериментальных точек относительно среднего

значения и линии регрессии одинаков, т.е. S y =S y_0CT (рис. 4.7, б).

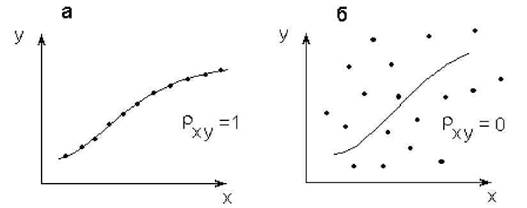
Рис. 4.7. Значения выборочного корреляционного отношения р_ху:

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА...

а - функциональная связь; б - отсутствие связи

3. Чем ближе расположены экспериментальные данные к линии регрес­сии, тем теснее связь, тем меньше остаточная дисперсия и тем больше корре­ляционное отношение.

Следовательно, корреляционное отношение может изменяться в преде­лах от 0 до 1.

Учитывая, что для компьютеров имеются пакеты программ для статисти­ческой обработки результатов исследований, рассмотрим методологию этого подхода на примере простейших линейных и одномерных задач (см. уравнение (4.5)). Идеология решения более сложных задач принципиально не отличается. Более того, как мы увидим в дальнейшем, многие нелинейные зависимости можно свести к линейным.