Интегрирование иррациональных выражений

Если подинтегральная функция рационально зависит от иррациональных выражений, то рекомендуется с помощью подстановки избавиться от них.

Примеры:

1.

Решение: применим подстановку, которая подинтегральное иррациональное выражение преобразует в выражение рациональное.

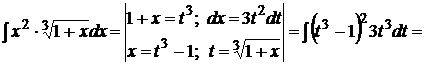
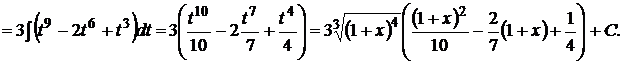
2. .

Решение:замена 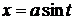позволяет выполнить преобразования, освободиться от квадратного корня и получить табличный интеграл.

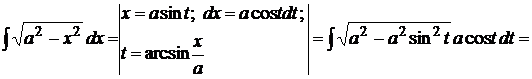
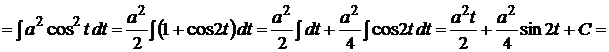
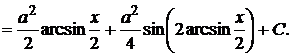
Так как

,

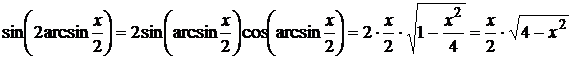получим

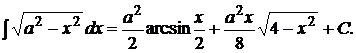
3. .

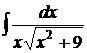Решение:

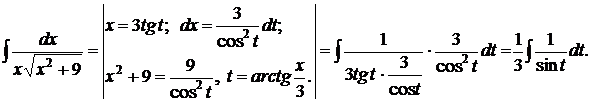
Полученный интеграл вычислим с помощью универсальной тригонометрической подстановки.

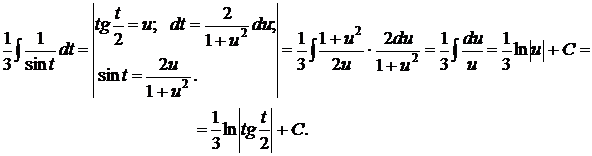
Вернувшись к переменной х, получим:

.

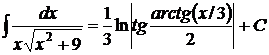Задания для самостоятельной работы

1. Вычислить интегралы от рациональных функций:

1.1. 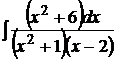; 1.2. 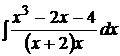; 1.3. ;

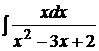1.4. 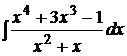; 1.5. .

2. Вычислить интегралы с помощью подстановок:

2.1. 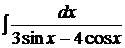; 2.2. 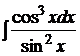; 2.3. 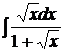; 2.4. ;

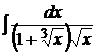2.5 .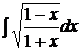

Вопросы для самоподготовки

1. Определение первообразной функции.

2. Определение неопределенного интеграла.

3. Свойства неопределенного интеграла.

4. таблица интегралов от элементарных функций.

5. Интегрирование подстановкой.

6. метод интегрирования по частям.

7. Интегрирование рациональных функций.

8. Интегрирование тригонометрических функций.

9. Интегрирование иррациональных функций.

Определённый интеграл

Интегральная сумма и определённый интеграл

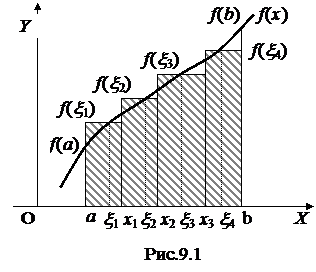Определение:Пусть функция f(x) определена и ограничена на отрезке [a;b]. Этот отрезок произвольно разобьём на n частей точками (рис.9.1)

а = х₀ < х₁ < х₂, <…< х_i <…<х_n-1 < х_n = b.

На каждом из частичных отрезков произвольно выберем точку x_I, вычислим значение f(x_i) и cоставим сумму

I = f(x₁)(х₁–a) + f(x₂)(х₂–х₁)+…+ f(x_i)(х_i–х_i-1)+…+ f(x_n)(b–х_n-1) = = 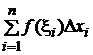, (Dх_i = х_i–х_i-1),

которая называется интегральной суммой функции f(х) на отрезке [a;b].

Определение: Предел интегральной суммы при условии, что число частичных отрезков неограниченно увеличивается, а длина наибольшего из них стремится к нулю, называется определённым интегралом функции f(x) в пределах от х = а до х = b и обозначается

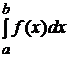= . (9.1)

Числа a и b называют нижним и верхним пределами интегрирования соответственно.

Если функция f(х) непрерывна на отрезке [a;b], то она интегрируема на этом отрезке, то есть предел (9.1) существует и не зависит от способа разбиения промежутка интегрирования [a;b] на частичные отрезки и от выбора точек x_i при каждом таком разбиении.

Геометрический и физический смысл определённого интеграла

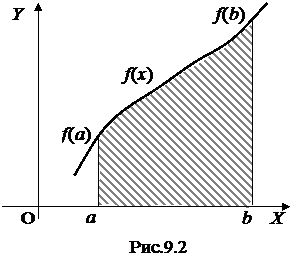
Если задана непрерывная на отрезке [a,b] функция у = f(x) (f(x)≥0), то определённый интеграл (9.1) представляет собой площадь криволинейной трапеции, ограниченной линиями: у = f(x), х = а, х = b и у = 0 (рис.9.2). Если f(x) < 0, то площадь берётся со знаком минус.

Пусть материальная точка движется в одном направлении со скоростью, изменяющейся по закону v = v(t). Тогда путь s, пройденный точкой за отрезок времени t₂ – t₁, вычисляется по формуле .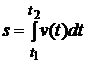

Если сила F, действующая на материальную точку, сохраняет направление движения, но величина её меняется в зависимости от пути s, то есть F = F(s), то работа находится по формуле

.
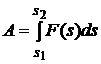