Отыскание исходного опорного решения.

Решение системы ограничений (1), (2) транспортной задачи будем записывать в транспортную таблицу следующим образом: значение неизвестной x_ij в клетку ij. Если в каждую клетку транспортной таблицы занесено некоторое число, то эта совокупность будет решением системы ограничений (1), (2), если все эти числа «≥0» и сумма чисел в каждой i-й строке равна запасу a_i, а сумма чисел в каждом j-м столбце равна потребности b_j, ввиду того, что ранг системы ограничений равен (m+n-1), опорное решение должно иметь более (m+n-1) отличных от нуля переменных. Клетки таблицы, в которой находятся отличные от нуля числа называются занятыми, остальные – свободными.

Рассмотрим построение исходного опорного решения системы (1), (2) методом северо-западного угла.

bj ai	b1	b2	…	bn
a1	x11
a2
…
am

Будем заполнять таблицу, начиная с клетки 11. Запишем в клетку 11 число, равное наименьшему из двух чисел a₁ и b₁ :

1) a₁<b₁

x₁₁=a₁

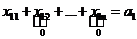
Поэтому остальные клетки первой строки закрыты для заполнения.

Первому потребителю нужно ещё (b₁-a₁) единиц груза. Будем удовлетворять оставшиеся потребности первого потребителя за счет запасов второго поставщика. От второго поставщика перевезём к первому потребителю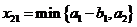

2) a₁>b₁, x₁₁=b₁ и остальные клетки первого столбца закрыты для заполнения.

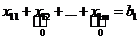
(a₁-b₁) – у первого поставщика останется такое количество груза. Этими запасами первого поставщика будет максимально удовлетворён второй потребитель.

В клетку 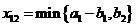. Заполнив клетку 12 или клетку 21, двигаемся из неё в соседнюю клетку либо вправо по строке, если окажется закрыт соответствующий столбец, ибо вниз по столбцу, если окажется закрытой соответствующая строка.

3) a₁=b₁, x₁₁=a₁=b₁. И закрываем либо первый столбец, либо первую строчку для дальнейшего заполнения. Процесс продолжается до тех пор, пока не будут удовлетворены все запросы b_j и не исчерпаются все запасы a_i.

Последняя заполняется клетка mn.

Замечание 1:

Может оказаться, что после занесения очередного числа x_ik закроется одновременно i-я строка и k-й столбец, тогда занесём в соседнюю строчке или столбцу клетку, ту из них, которой соответствует наименьший тариф перевозки, запишем в ней «0». Такие нули, в отличие от нулей свободных клеток, будем называть базисными нулями.

Замечание 2:

Совокупность чисел x_ik, найденных методом СЗУ, есть решение системы ограничений транспортной задачи, т.к. при заполнении таблицы выполнялись равенства по строчкам и столбцам, соответствующие уравнениям системы (1), (2).

Пример:

Составить исходное опорное решение.

bj ai

m=4

n=5

m+n-1=8

Теорема:

Решение, построенное методом СЗУ является опорным.

Доказательство:

Для этого достаточно доказать, что совокупность заполненных клеток образует совокупность базисных клеток.

1) Доказать: заполненных клеток m+n-1.

2) Доказать: вектор-столбцы коэффициентов при неизвестных с номерами заполненных клеток линейно независимы.

1. На каждом этапе, кроме последнего, занесением очередного значения x_ik в транспортную таблицу закрывается только один столбец или только одна строка. И только в последней клетке таблицы mn одновременно закрываются n-я строка и m-й столбец. Следовательно, всего будет занесено в таблицу чисел x_ik на единицу меньше, чем имеется строк и столбцов в таблице.

2. Методом математической индукции по числу: k=2, (m=1, n=1)

b a	b1
a1	x11

Будет заполнена только одна клетка x₁₁ и вектор b₁₁ при неизв. Образует линейно независимую систему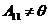

Предположение индукции:

Пусть утверждение (2) выполняется при k=m+n-1. Докажем, что будет выполняться и при k=m+n. Будем заполнять транспортную таблицу методом СЗУ и пусть для опред. x₁₁=a₁₁

Первая строчка закрыта, пусть будут заполнены (1,1), (2,1),…,(i,j),…,(m,n).

Выпишем вектор-столбцы, соответствующие клеткам с этими номерами.

bj ai	b1	b2	…	bj	…	bn
a1	x11
a2	x21
… ai … am

(*)

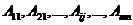
Докажем, что эти векторы линейно независимы.

Линейная комбинация:

(1)

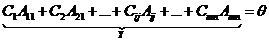
Первая координата у вектора Y: у всех векторов системы (*), кроме вектора А₁₁ первые координаты равны нулю, т.к. у них первый индекс больше единицы.

С₁=0

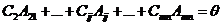(2)

Из исходной таблицы вычеркнем первую строчку и изменим потребности первого потребителя на b₁-a₁. Получим новую транспортную задачу, у которой число поставщиков равняется m-1, число потребителей n.

Тогда k=m+n-1.

Выпишем вектор-столбцы при неизвестных с номерами заполненных клеток.

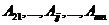
По предположению индукции эти векторы линейно независимы.

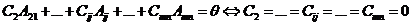
Тогда в (1) получаем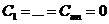

Из доказанного в (1) и (2) следует, что решение, построенное методом СЗУ является опорным.

Циклы и их взаимосвязь с линейной зависимостью векторов условий задач.

При построении опорного решения и для перехода от одного опорного решения к другому используют понятие цикла.

Цикл – такая последовательность клеток транспортной таблицы, в которой две и только две соседние клетки расположены в одной строке или столбце, причем первая и последняя клетки также находятся в одной строке или одном столбце.

Цикл изображается в транспортной таблице в виде замкнутой ломаной линии. В цикле любая вершина является угловой, в которой происходит оборот на .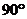

Теорема:

Допустимое решение является опорным, если никакая часть занятых им клеток не образует цикла.

Без доказательства.

Теорема используется для того, чтобы проверить, что допустимое решение является опорным.

На этой теореме основан метод вычёркивания:

базисный нуль

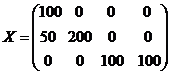
Вычеркнем все строчки таблицы, содержащие по одной занятой клетке. В оставшейся части таблицы вычеркнем все столбцы, содержащие по одной занятой клетке. Затем снова возвращаемся к строчкам и вычеркиваем в оставшейся части таблицы все строчки, содержащие по одной занятой клетке.

Если в результате вычёркивания все строчки и столбцы будут вычеркнуты, значит, из занятых клеток таблицы нельзя выделить часть, образующую цикл, и система соответствующих векторов-условий линейно независима, а решение является опорным.

Если же после вычёркиваний остаётся часть клеток, то эти клетки образуют цикл, система соответствующих векторов-условий является линейно зависимой, а решение не является опорным.

Пример невычёркиваемого плана:

	*

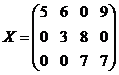
Решение не является вычёркиваемым.

Достаточное условие оптимальности решения транспортной задачи.

Пусть исходное опорное решение записано в транспортной таблице, тогда в базисных клетках будут стоять неотрицательные числа, а свободные клетки не заполнены (соответствующие им неизвестные равны нулю).

Сопоставим каждому поставщику a_i некоторое неизвестное число 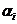, а каждому потребителю b_j -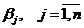

Найдём эти неизвестные числа из условия, что для каждой базисной клетки ij выполняется условие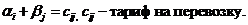

(*)

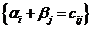m+n-1 – уравнений

поставщиков – m+n.

Известно, что линейная система алгебраических уравнений, в которой неизвестных больше, чем уравнений, является неопределённой.

Для (*), чтобы найти какое-то решение, надо задать какое-то одно неизвестное, а все остальные находить из системы. Всякое решение системы (*) называется потенциалами данного опорного решения.

Пример:

Построить опорное решение и найти его потенциал.

bj ai	b1=30	b2=25	b3=35	b4=20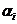
a1=50
a2=40
a3=20

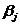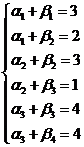
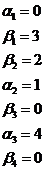
Теорема:

Пусть Х₀ – опорное решение системы ограничений (1), (2).

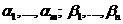- потенциалы этого опорного решения.

Если для каждой свободной клетки выполняется условие: 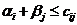, то решение Х₀ является оптимальным.

Доказательство:

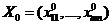, пусть для допуст. реш.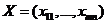

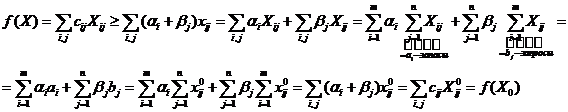
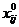[ - для любого решения выполняется условие (1) и(2)]

Для базисных клеток транспортной таблицы 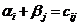, а если клетка – свободная, то 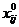=0.

Если имеется хотя бы одна свободная клетка, для которой не выполняется условие 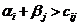, то опорное решение не является оптимальным, и необходимо перейти к новому опорному решению, на котором значение целевой функции будет меньше. Переход от одного опорного решения к другому осуществляется при помощи цикла. Определяется клетка транспортной таблицы, которой соответствует 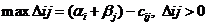, строится цикла пересчёта, начиная с выбранной клетки ij, а остальные вершины цикла – в клетках, занятых опорным решением (не обязательно вершины цикла пересчёта занимают все базисные клетки). Обойдём цикл пересчёта, начиная с клетки ij, против часовой стрелки, и расставим в вершинах цикла поочерёдно «+» и «-», причём «+» в кл. ij. Увеличим все значения неизвестных в положительных вершинах цикла и уменьшим все значения неизвестных в отрицательных вершинах цикла на число ρ, равное наименьшему из чисел, расположенных в клетках – вершинах цикла, обозначенных знаком «-». Клетка со знаком «-», в которой достигается минимальное значение, остаётся пустой. Если min достигается в нескольких клетках, то одна остаётся пустой, а в остальных – базисные нули с тем, чтобы число занятых клеток оставалось m+n-1.