ОДР n-мерной задачи линейного программирования.

При анализе систем линейных уравнений с n неизвестными широко используется понятие n-мерных векторов или точек n-мерного пространства.

Введём n-мерное векторное (линейное) пространство Rⁿ. Элементами этого пространства являются возможные наборы из n действительных чисел, взятых в определённом порядке.

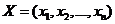- вектор или точка пространства Rⁿ.

x₁,x₂,…,x_n – координаты вектора или точки.

В Rⁿ определяются операции сложения элементов и умножения элементов на число.

I. X+Y=(x₁+y₁,x₂+y₂,…,x_n+y_n)

II.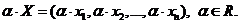

Вводится вектор-нуль

1) θ=(0,0,…,0)

2) вектор, противоположный X (-X): X+(-X)=θ.

Операции I и II обладают следующими свойствами:

1) Коммутативность X+Y=Y+X.

2) Ассоциативность сложения X+(Y+Z)=(X+Y)+Z.

3) Ассоциативность умножения 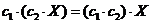, с₁,c₂ – действительные числа.

4) Дистрибутивность

А) векторная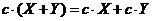

Б) скалярная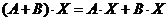

По аналогии с двух- и трёхмерными векторами в Rⁿ можно ввести понятие скалярного произведения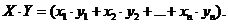

Наличие скалярного произведения в Rⁿ позволяет ввести понятие длины вектора и расстояния между элементами Rⁿ. Длиной вектора (его модулем) наз. « 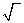» из скалярного квадрата.

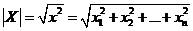
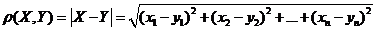
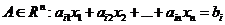
A(x₁,x₂,…,x_n) – каждый из которых является решением линейного уравнения относительно n переменных, называется гиперплоскостью.

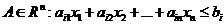
A(x₁,x₂,…,x_n) – называется полупространством, расположенным по одну сторону от граничной гиперплоскости.

R³

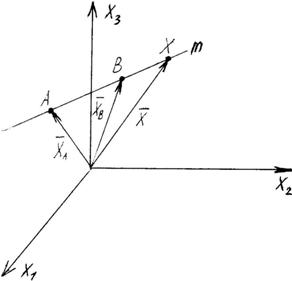
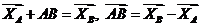
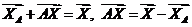
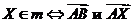- коллинеарные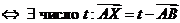

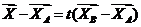
Выведем уравнение отрезка, расположенного на прямой.

Параметрическое уравнение прямой m - (*)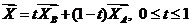

Если 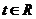, то (*) определяет прямую линию m.

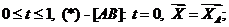
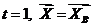
0<t<1 – внутренние точки отрезка [AB]

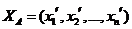- радиус-вектор точки А из Rⁿ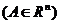

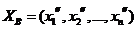- радиус-вектор точки B из Rⁿ .

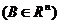Определение. Отрезком 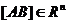, соединяющим точки A и B, называется множество точек этого пространства, радиус-векторы которых определяются уравнением (*).

Определение. Множество M называется выпуклым, если вместе с любыми своими двумя точками A и B она содержит и все точки отрезка AB, их соединяющего.

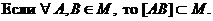
Пример:

1. На плоскости

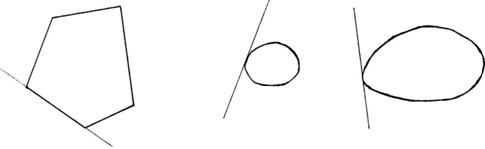2. Невыпуклые множества

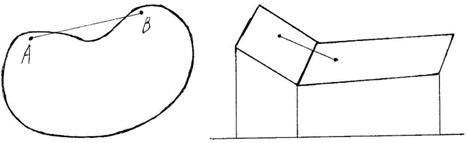Теорема 1.

Пусть M₁ и M₂ – выпуклые множества и их пересечение – непустое множество 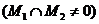, тогда 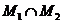- выпуклое множество.

Доказательство:

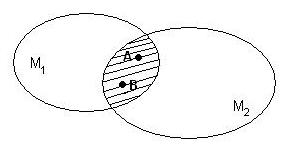
Возьмём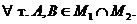

Доказать: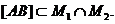

Т.к.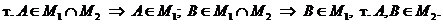

Т.к. множества M₁ и M₂ – выпуклые, то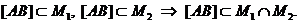

Следствие:

Пересечение конечного числа выпуклых множеств – выпуклое множество.

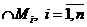- выпуклое множество.

M₁, M₂,..., M_n.

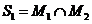
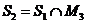- выпуклое

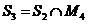
Теорема 2.

Область решений системы линейных уравнений и неравенств есть выпуклое множество.

1) Докажем, что ОР одного уравнения с n неизвестными, которое определяет гиперплоскость в Rⁿ – есть выпуклое множество.

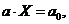(1)

Где 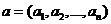- вектор из неизвестных.

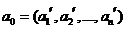
Пусть 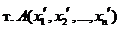и 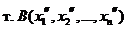- решение (1).

Т.е. т. А и т. В – точки, принадлежащие ОР уравнения (1).

Возьмём любую точку С внутри [AB]. Её координаты определяются из равенства 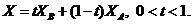Проверим, что эта т. С также является решением уравнения (*).

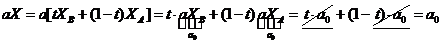
Т. С является решением уравнения (1). Вместе с двумя точками А и В ОР уравнения (1) содержит все точки отрезка [AB]. ОР уравнения (1) – выпуклое множество.

Докажем, что ОР одного линейного неравенства с n переменными, т.е. полупространство n-мерного пространства также есть выпуклое множество.

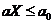2) (2)

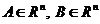- решение (2)

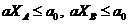
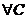внутри [AB] и проверяем, что эта точка также является решением (2)

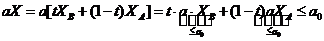
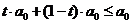
т. С является решением (2) и все точки отрезка [AB] принадлежат полупространству, которое определяется неравенством (2).

Теорема 3.

Область решений системы из линейных уравнений и неравенств есть выпуклое множество. Эта область есть пересечение конечного числа гиперплоскостей и полупространств, и по теореме 2 – есть также выпуклое множество.

Следствие.

ОДР ЗЛП – есть выпуклое множество.

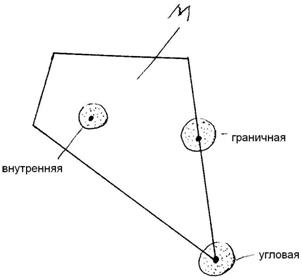
Во всяком выпуклом множестве можно выделить внутренние, граничные и угловые точки.

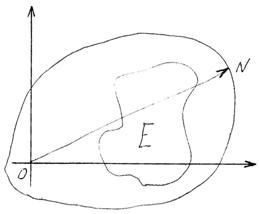
Т. А называется внутренней точкой множества М, если существует окрестность этой точки, которая принадлежит множеству М.

Т. А – внутренняя точка множества М, если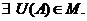

А – граничная точка множества М, если 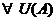имеются как точки множества М, так и точки, не принадлежащие этому множеству М.

Т. А – угловая точка выпуклого множества М, если она не является внутренней ни для какого отрезка, соединяющего две другие точки множества.

Множество, содержащее все свои граничные точки, называется замкнутым.

Множество М, называется ограниченным, если , что для каждой точки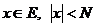

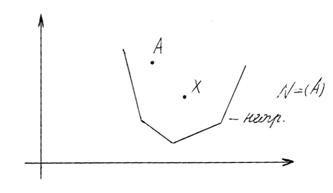
Множество может быть замкнутым, но неограниченным и наоборот. Например: гиперплоскость - замкнутое неограниченное множество.

Определение.

Выпуклое множество, являющееся пересечением конечного числа полупространств, называется выпуклым многогранником.

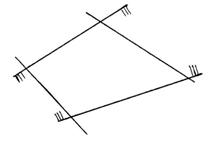- не является выпуклым множеством, т.к. является пересечением бесконечного числа граней.

- выпуклый многогранник

Т.к. полупространство определяется линейными неравенствами, то можно сказать, что выпуклый многогранник – это множество, которое определяет конечная система линейных равенств. Т.о., ограничение ЗЛП в виде (1) и (2) определяют n-мерный выпуклый многогранник.

(1)

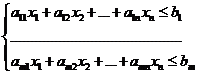
(2)

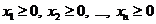
Т.к. все неравенства систем (1) и (2) – нестрогие, то эти неравенства содержат точки, лежащие на граничных гиперплоскостях, т.е. являются замкнутыми.

При решении n-мерной ЗЛП удобно использовать каноническую форму записи. Т.к. систему линейных неравенств (1) можно заменить эквивалентной ей системой линейных уравнений, то мы приходим к выводу, что областью допустимых решений n-мерной ЗЛП является n-мерный выпуклый многогранник, поэтому геометрически ЗЛП – есть задача отыскания максимума (минимума) линейной функции на выпуклом многограннике.

Теорема 1 (о существовании опорного решения).

Если система линейных уравнений (1) имеет хотя бы одно допустимое решение, то среди этих решений есть хотя бы одно опорное.

Доказательство:

Систему линейных уравнений (1) запишем в векторной форме

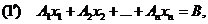
Где А₁ – вектор-столбец из коэффициентов при неизвестных … .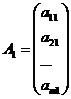

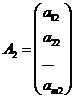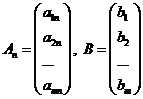Пусть ранг векторов системы .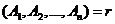

Для определённости будем считать, что первые n векторов этой системы образуют базис. Это означает, что существует общее решение системы (1), где 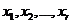- базисные, 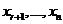- свободные; сущ. базисн. реш. 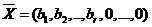. (2)

Последние n-r координат вектора 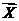равны нулю.

Если первые координаты вектора 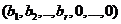неотрицательны, то это базисное решение является ещё и опорным решением системы (1). Докажем, что система (1) имеет опорное решение указанного вида (2).

По условию теоремы 1 существует хотя бы одно допустимое решение системы (1).

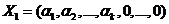
Возможны следующие два случая:

1) 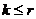, 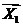- опорное. Т.к. n-r последних координат X₁ равны нулю 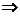X₁ – базисное решение. Кроме того, первые r координат неотрицательны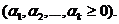

2) 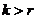. В этом случае X₁ – допустимое решение, но не базисное, т.к. число последних нулевых координат меньше, чем k-r.

Т.к. X₁ – решение, поэтому 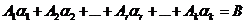(а)

Отметим, что система векторов 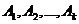линейно зависима, т.к. в этой системе число векторов k>r - ранг системы векторов 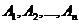, значит, существует нетривиальная линейная комбинация.

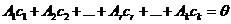(б)

есть нулевой вектор.

Утверждение: хотя бы одно из этих чисел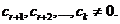

Противное:

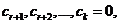тогда существует неравный нулю коэффициент: среди чисел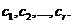 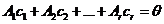, комбинация – нетривиальная.

Противоречие.

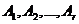- образуют базис, и только тривиальная комбинация линейных векторов даёт нуль-вектор.

Из уравнения (а) вычтем уравнение (б), умноженное на λ.

(а)-λ (б)

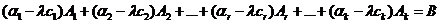
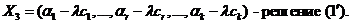
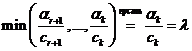
k-я координата вектора X₃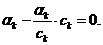

Все остальные координаты вектора X₃ «≥0».

В результате решений X₃ число нулевых свободных переменных увеличилось хотя бы на единицу. Если это останется меньше, чем (n-r), то процедуру надо повторить до тех пор, пока не придём к вектору, у которого число последних нулевых координат равно (n-r), то есть тем самым найдём опорное решение.

Теорема 2.

Допустимое решение ЗЛП является угловой точкой ОДР тогда и только тогда, когда это решение – опорное.

Пусть дана ЗЛП и пусть системы ограничений (1) и (2) определяют выпуклый многогранник М.

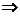Пусть 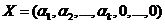- угловая точка М

все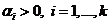

1. 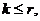тогда из теоремы 1 мы получаем, что это решение является опорным.

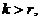
2. 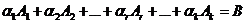(а)

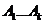- лин. завис.

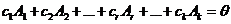(б)

Уравнение (а) ± уравнение (б) 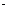t, t – число, большее нуля.

(с)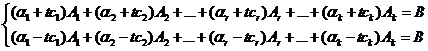

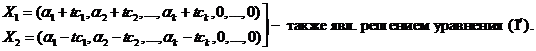
Подберём число t так, чтобы все координаты векторов X₁ и X₂ были неотрицательными.

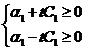
1. с₁>0

Из первого неравенства системы получаем, что .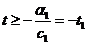

Из второго неравенства системы получаем, что .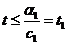

2. с₁<0

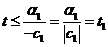
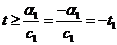
Если 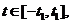то первые координаты будут неотрицательными.

Решив систему , (*)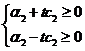

найдём отрезок [-t₂,t₂], для каждой точки которого выполняется неравенство (*).

Выполним этот процесс для всех ненулевых координат векторов X₁ и X₂.

Найдём k чисел t₁,t₂,…,t_k.

Среди этих чисел возьмём наим. 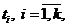тогда на [-t_i,t_i] все координаты X₁ и X₂ будут неотрицательными, это означает, что X₁ и X₂ принадлежат ОДР, т.е. это две точки многогранника М.

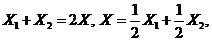это означает, что точка X – середина отрезка, концами которого являются т. X₁ и т. X₂, т.е. т. X не является угловой точкой по определению угловой точки.

Получим противоречие, т.к. т. X – угловая по определению.

Необходимость:

Докажем, что опорн. реш. явл. углов. т. многогранника М.

Пусть 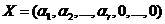- угловая точка М.

Противное:

Х не является угловой точкой, это означает, что существует отрезок в многограннике, для которого Х – внутренняя точка.

Пусть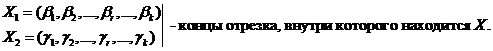

Т.к. Х – внутренняя точка отрезка Х₁Х₂, то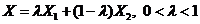

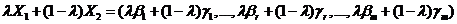
Поскольку у вектора Х последние (n-r) координаты – нулевые, значит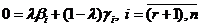

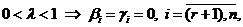т.о. каждое из допустимых решений Х₁Х₂ содержит нулевые значения для тех же свободных переменных, что и решение Х.

Т.к. значения свободных переменных однозначно определяют решение системы, то Х=Х₁=Х₂, т.е. мы доказали, что т. Х может быть только концом отрезка. Получили противоречие с предположением о том, что Х - внутренняя точка 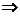опорное решение Х есть угловая точка.

Выпуклая линейная комбинация системы векторов.

Определение. Пусть X₁,X₂,…,X_s – система n-мерных векторов.

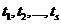- числа:

1)

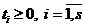
2)

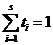
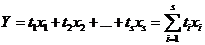- выпуклая линейная комбинация системы векторов Х₁,…,X_s.

Примеры:

1. 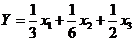- выпуклая линейная комбинация.

2. 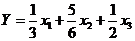- не выпуклая линейная комбинация.

3. 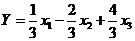- не выпуклая линейная комбинация.

Теорема 3.

Множество точек ограниченного выпуклого n-мерного многогранника совпадает с множеством выпуклых линейных комбинаций его угловых точек.

Без доказательства.

Теорема содержит два утверждения:

Если х₁,х₂,…,х_s – угловые точки многогранника М, то любая точка х из многогранника М.

1. .

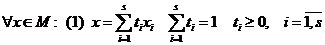2. Любая точка х, определяемая равенством (1) при условии, что х₁,х₂,…,х_s – угловые точки многоугольника М

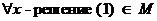
Например, отрезок – многогранник, порождённый двумя точками (своими концами) и т.д.

Существенно то, что многогранник – ограниченный, для неогран. теорема не выполняется.