Общая формулировка задач линейного программирования.

Общая формулировка задач линейного программирования.

Найти вектор X=(x₁,x₂,…,x_n), который удовлетворяет системе линейных ограничений и обеспечивает экстремальное (минимальное или максимальное) значение целевой функции. Ограничения могут быть сформулированы в виде равенств или неравенств. В зависимости от этого различают различные формы записи задач линейного программирования.

1. Общая форма записи ЗЛП.

Дано: система линейных ограничений, в которой S равенств и (m-S) неравенств

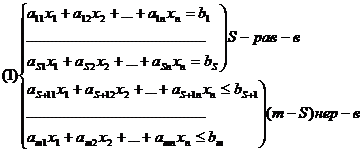
(2)

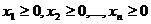
(3)

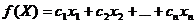
Требуется найти такое решение системы (1) X=(x₁,x₂,…,x_n), которое удовлетворяет условию (2), и на котором целевая функция достигает экстремума (максимума или минимума).

1. Симметричная форма.

В ней ограничение (1) содержит только неравенства

(3)

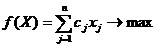
(1) 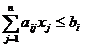i=1,2,…,m

(2)

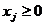
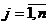
(3)

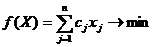
(1) 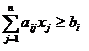i=1,2,…,m

(2)

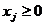
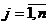
1. Каноническая форма.

Ограничение (1) содержит только равенства

(3)

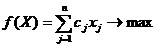
(1) 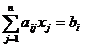i=1,2,…,m

(2)

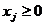
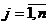
Определение. Вектор X=(x₁,x₂,…,x_n), координаты которого являются решением ограничений (1) и (2), называется допустимым решением ЗЛП. Множество всех допустимых решений задачи называется областью допустимых решений (ОДР). Допустимое решение X, на котором целевая функция достигает максимума или минимума, называется оптимальным решением задачи.

Переход от одной формы записи ЗЛП к другой.

Теорема. Пусть дано линейное неравенство с n переменными 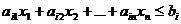(4)

и переменная 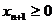(5)

такая, что 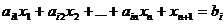, (6)

тогда .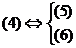

Доказательство: (достаточность)→:

Пусть X=(α₁, α ₂,…, α _n) – решение (4), т.е. 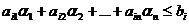(4’)

Введём α_n+1 =b_i- 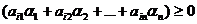, (5’)

при этом 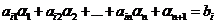. (6’)

Пусть выполняется (5’) и (6’). Отбросив в левой части уравнения (6’) 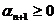, получим неравенство (4’).

Теорема позволяет от неравенств в системе ограничений перейти к уравнениям и, наоборот, от уравнения перейти к неравенству.

Симплексный метод.

Пример.

Найти max функции при усл.

(1)

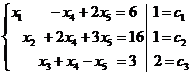
(2)

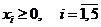
(3)

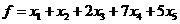
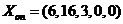
(4)

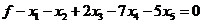
Умножим соответствующие уравнения системы (1) на соответствующие числа (коэф.) и сложим с равенством (4).

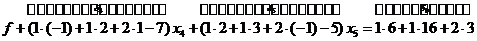
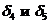- числа, оценки свободных переменных

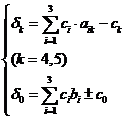
(5) 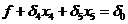х₄=х₅=0 f(Х_оп)=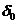

(5) - приведённое выражение для линейной функции.

Т.к. для опорн. реш. значения всех свободных переменных равны нулю, то, положив в равенстве (5) значения свободных переменных равными нулю, мы сразу находим значение линейной функции на данном опорном решении.

Определение. Говорят, что ЗЛП приведена к симплексной форме, если сис. ограничительных уравнений разрешена относительно базисных неизвестных, свободные члены уравнений «≥0», а линейная функция выражена через свободные неизвестные. ← Отыскав исходн. опорн. реш., и получив приведённое выражение лин. функции, мы привели ЗЛП к симплексной форме.

Перепишем сист. лин. уравнений (2) в виде таблицы, добавив к ней в качестве последней строки строчку с коэффициентами значения (5), считая что уравнение разрешено относительно базисной переменной f.

ci	Баз. неиз.				-2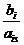
bi	x1	x2	x3	x4	x5
	x1 x2 x3					-1	-1
	f					-4	-2

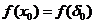
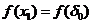
Теорема.

Пусть ЗЛП записана в симплексной форме, тогда:

1⁰. 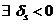и в каждом столбце с такой оценкой имеем хотя бы один положительный элемент, тогда решение можно улучшить, т.е. перейти к опорному решению Х₁, в котором значение линейной функции будет больше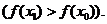

2⁰. Существует отрицательная оценка свободных переменных такая, что столбец которой не содержит положительных элементов, то ЗЛП 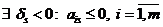не имеет решения ввиду неограниченности целевой функции в ОДР.

3⁰. Все оценки свободных переменных «≥0». В этом случае соответствующее опорное решение будет оптимальным.

Все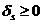

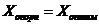
Доказательство:

П.1. Найдём в симплексной таблице элемент 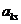из следующих условий:

1) s-й столбец: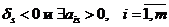

2) k-я строка: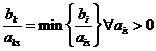

С разрешающим элементом a_ks выполним преобразование однократного замещения.

x_s→базисн., x_k-своб.неизв.

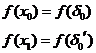
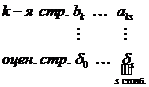
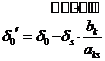
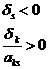
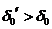
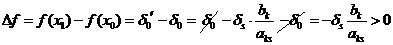
П.2. Пусть ЗЛП приведена к симплексной форме, и система ограничительных уравнений разрешена относительно базисн. неизв., и все свободные члены неотрицательны.

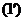
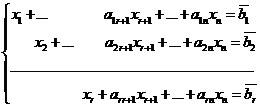
Построим какое-либо неотрицательное решение Х системы .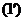

Возьмём для своб. перем. следующие неотрицательные значения.

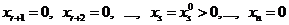
Из системы 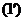найдём значения базисн. неизв.

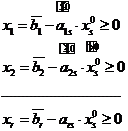
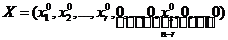
Получим неотриц. реш. системы 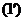. Теперь, используя приведённое выражение для линейной функции, мы получим значение линейной функции на построенном решении.

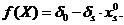
Из этого равенства видно, что если переменной x_s придать сколь угодно большие значения, то значение лин. функции можно сделать сколь угодно большим положительным числом, т.о. линейная функция не ограничена сверху в ОДР.

П.3. Все оценки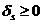

Пусть Х₀ – соответствующее опорное решение. Требуется доказать, что для любого другого опорного решения Х₁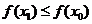

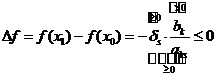
Признак существования множества оптимальный решений.

Если все оценки свободн. перем. 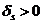, то введение любой переменной в базис приведёт к уменьшению функции f, т.к. 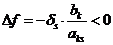и, следовательно, существует только одно оптимальное решение.

Если же какая-то оценка свободной переменной окажется равной нулю 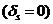, то введение переменной х_s в базис не изменит значение линейной функции f, т.к. 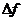будет «=0», и поэтому можно перейти к новому опорному решению, для которого 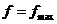, т.о. признаком существования множества решений является наличие хотя бы одной нулевой оценки свободных переменных при неотрицательности всех остальных оценок.

Если нулевых оценок окажется несколько, то введением в базис кажд. из соотв. своб. перем. можно найти несколько оптимальных решений.

Транспортная задача

Формулировка задачи.

В m 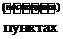сосредоточен однородный груз в количествах 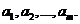Этот груз нужно перевезти n потребителям в количествах 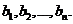Известны числа 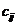- стоимость перевозки единицы груза от i-го поставщика j-му потребителю (тариф перевозки).

Будем считать, что потребности в грузе равны его запасам: 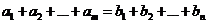(задача с правильным балансом).

Обозначим 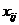- объём груза, перевозимого от i-го поставщика j-му потребителю.

Условия транспортной задачи будем записывать в виде транспортной таблицы.

bj ai	b1	b2	…	bn
a1	c11	c12	…	c1n
a2	c21	c22	…	c2n
…
am	cm1	cm2	…	cmn

Введём вектор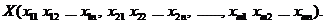

Х – план перевозок.

План перевозок должен удовлетворять следующим условиям

1.

(1)

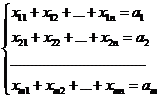
Условие (1) – требование того, чтобы грузы от каждого поставщика были вывезены полностью.

2.

(2)

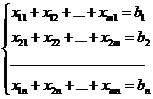
Условие (2) – требование того, чтобы запросы каждого потребителя были полностью удовлетворены.

(3)

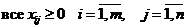
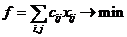
Математическая формулировка транспортной задачи:

Найти такой план Х, удовлетворяющий системам ограничений (1) и (2), условиям неотрицательности (3) и обеспечивающий минимум целевой функции f.

Симплекс-процесс:

1. Определение исходного опорного решения.

2. Оценка этого решения.

3. Переход к лучшему решению путём однократного замещения одной базисной переменной на свободную.

Однако специфичность системы ограничений (1) , (2) позволяет систематизировать для её решения более простой вычислительный алгоритм, чем симплексный метод.

Особенности системы ограничений (1), (2):

1. Коэффициенты при неизвестных (1), (2) равны единице.

2. Каждая неизвестная встречается в двух и только двух уравнениях, причем одно из уравнений входит систему (1), а другое – в (2).

Общая формулировка задач линейного программирования.

Найти вектор X=(x₁,x₂,…,x_n), который удовлетворяет системе линейных ограничений и обеспечивает экстремальное (минимальное или максимальное) значение целевой функции. Ограничения могут быть сформулированы в виде равенств или неравенств. В зависимости от этого различают различные формы записи задач линейного программирования.

1. Общая форма записи ЗЛП.

Дано: система линейных ограничений, в которой S равенств и (m-S) неравенств

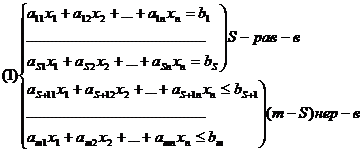
(2)

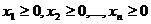
(3)

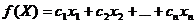
Требуется найти такое решение системы (1) X=(x₁,x₂,…,x_n), которое удовлетворяет условию (2), и на котором целевая функция достигает экстремума (максимума или минимума).

1. Симметричная форма.

В ней ограничение (1) содержит только неравенства

(3)

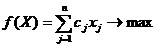
(1) 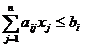i=1,2,…,m

(2)

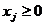
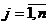
(3)

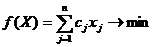
(1) 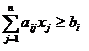i=1,2,…,m

(2)

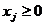
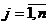
1. Каноническая форма.

Ограничение (1) содержит только равенства

(3)

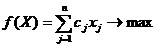
(1) 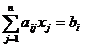i=1,2,…,m

(2)

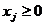
Определение. Вектор X=(x₁,x₂,…,x_n), координаты которого являются решением ограничений (1) и (2), называется допустимым решением ЗЛП. Множество всех допустимых решений задачи называется областью допустимых решений (ОДР). Допустимое решение X, на котором целевая функция достигает максимума или минимума, называется оптимальным решением задачи.