Понятие о внутренней геометрии поверхности

Рассмотрение двух поверхностей, полученных изгибанием, показывает, что многие их свойства одни и те же, хотя формы у поверхностей разные. Поэтому целесообразно изучать такие понятия и факты теории поверхностей, которые не меняются при изгибании.

Определение. Внутренней геометрией поверхности называется совокупность таких её свойств, которые определяются только коэффициентами первой квадратичной формы, то есть не меняются при изгибании.

К внутренней геометрии относятся:

– длины кривых на поверхности;

– углы между кривыми;

– площади областей поверхности;

– гауссова кривизна: K =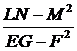

LN – M² = +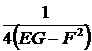

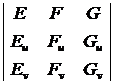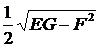
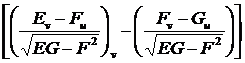
Гауссову кривизну можно найти, используя только коэффициенты первой квадратичной формы, таким образом, две поверхности с одинаковой гауссовой кривизной изометричны.

– тип точек на поверхности и др.

Геодезическая кривизна кривой на поверхности

Пусть Ф – регулярная поверхность, g Ì Ф – регулярная кривая, 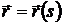– её естественная параметризация, М Î g – некоторая точка.

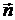– единичный вектор нормали к поверхности.

Определение. Число k_g = ( 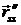, , 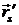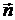) называется геодезической кривизной кривой g в точке М.

Геометрический смысл геодезической кривизны: k 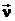– вектор кривизны кривой g в точке М, геодезическая кривизна кривой – это длина проекции вектора кривизны k 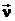на касательную плоскость (с точностью до знака).

Геодезическая кривизна в произвольной параметризации

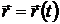– параметризация кривой g;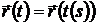

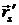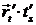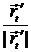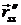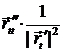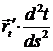= = ; = + => k_g =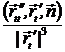

Пример. Найти геодезическую кривизну винтовой линии u = u₀, лежащей на прямом геликоиде x = u cos v, y = sin v, z = bv.

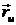(cos v; sin v; 0), 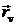(–u₀ sin v; u₀ cos v; b)

( ; – ; )

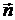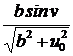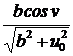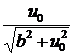Пусть t = v => 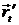= 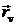, 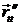= (–u₀ cos v; –u₀ sin v; 0), | | =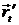

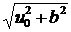
k_g = = –

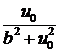
Геодезические линии

Определение. Линия на поверхности называется геодезической, если в каждой её точке геодезическая кривизна равна нулю.

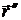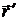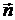( , , ) = 0 (в любой параметризации)

Свойства геодезической линии

1. Кривая g является геодезической тогда и только тогда, когда в каждой её точке, где кривизна k ¹ 0, имеет место соотношение 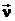|| 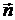(вектор кривизны коллинеарен нормали).

2. Пусть g – линия касания двух поверхностей Ф₁ и Ф₂. g – геодезическая линия для Ф₁ тогда и только тогда, когда g – геодезическая линия для Ф₂.

3. Через каждую точку регулярной поверхности в любом направлении можно провести, причем единственную геодезическую линию.

4. Геодезическими линиями на сфере являются большие окружности и только они.

Пример. Найти геодезические линии на прямом круговом цилиндре:

х = R cos u, y = R sin u, z = v (0 £ u < 2p, –¥ < v < ¥)

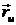(–R sin u, R cos u, 0), 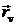(0; 0; 1); 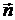(cos u; sin u; 0)

Пусть 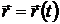– параметризация линии, лежащей на цилиндре, то есть u = u(t),

v = v(t).

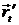(–R sin u · u_t'; R cos u · u_t'; v_t');

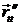(–R cos u (u_t')² – R sin u · 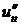; –R sin u · (u_t')² + R cos u · ; )

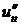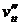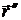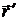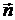( , , ) = 0 => u_t' 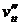– 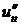v_t' = 0

Решением этого дифференциального уравнения являются: u = at + b, v = ct + d.

Тогда на цилиндре геодезическими линиями будут:

x = R cos(at + b), y = R sin(at + b), z = ct + d – винтовые линии

Теорема (основное свойство геодезической линии). Если точки P и Q геодезической линии на поверхности Ф достаточно близки, дуга М₁М₂ этой линии является кратчайшей среди дуг всевозможных кривых на Ф с концами P и Q.

Замечание. Требование близости точек P и Q на геодезической линии существенно. Достаточно рассмотреть две дуги большой окружности на сфере с общими концами P и Q, не являющимися диаметрально противоположными точками. Одна из этих дуг является кратчайшей, а другая – нет.