Прямолинейное движение с постоянным ускорением. Определение положения свободной поверхности при движении сосуда.

ГИДРОСТАТИКА-3

Вопросы к лекции:

Относительный покой жидкости .Прямолинейное движение с постоянным ускорением. Определение давления в любой точке.

Прямолинейное движение с постоянным ускорением. Определение положения свободной поверхности при движении сосуда.

Вращение сосуда с постоянной угловой скоростью. Определение положения свободной поверхности при равномерном вращении сосуда с жидкостью.

Вращение сосуда с постоянной угловой скоростью. Определение давления в любой точке.

Вращение сосуда с постоянной угловой скоростью. Определение силы давления жидкости на дно, крышку, стенку.

Вращение сосуда с постоянной угловой скоростью. Свойства параболоида.

Вращение сосуда с постоянной большой угловой скоростью.

Относительный покой жидкости.

Прямолинейное равноускоренное движениесосуда с жидкостью.

При прямолинейном движении цистерны с жидкостьюна частицы жидкости, кроме сил тяжести действуют силы инерции, при этомповерхность жидкости принимает новое положение равновесия - положение относительного покоя.

Определение давления в любой точке.

Проекции единичных массовых сил на оси (рис.4.1б)

Ox: X =- jCosα=-aCosα, (4.9)

Oz :Z =-( jSinα+g)=-(αSina+g), (4.10)

Оу: Y = 0. (4.11)

При подстановке этих проекций в дифференциал давления, получим

dp = ρ [– (aCosα)dx -(aSinα+g)dz]= –ρ[ (aCosα)dx+(aSinα + g)dz]. (4.12)

Проинтегрировав этот дифференциал, получим выражение для давления

Р = -ρ[aCosα*x+(aSinα + g)*z] + С. (4.13)!!!

При начальных условиях: х₀, z₀,Po, (рис.4.1а) получим

C = P₀+ρ[aCosα*x_o+(aSinα + g)*z₀],(4.14)

подставляемСв (4.13).

Давление в любой точке жидкости, находящейся в относительном покое при прямолинейном равноускоренном движении.

Р = P₀+ρ[(aCosα)*(x₀-х)+(aSinα + g)*(z₀ – z)]. (4.15)

Определение силы давления жидкости на стенку, дно или крышку

Оси координат выбираем наиболее удобным образом на рис.4.10 ось Z- ось вращения, ось r - по поверхности крышки.

Для определения силы давления жидкости на дно или крышку выражаем силу, действующую на элементарную кольцевую площадкуdS =2πrdr радиусом r и ширинойdr. Давление в любой точке ось rвыбрана по верхней крышке:

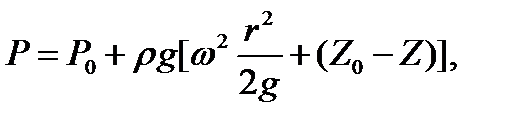
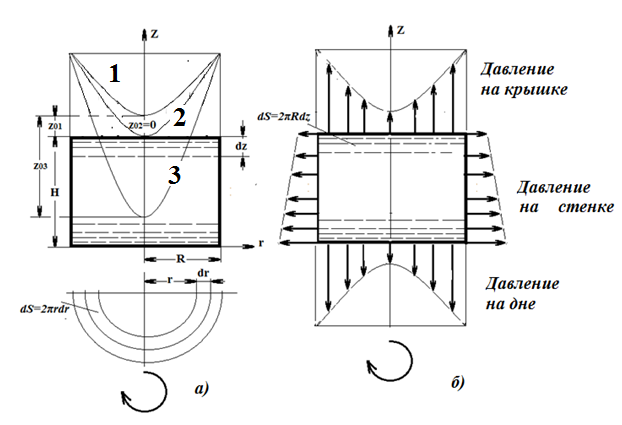Рис.4.10.Определение сил на крышку и дно сосуда(а).Эпюры давлений на крышку, стенку и дно сосуда(б). 1,2,3 – возможное расположение свободной поверхности параболоида относительно крышки.

При определении сил давленияна крышку Z=0, возможны следующие варианты расположения параболоида

1) Z₀₁> 0: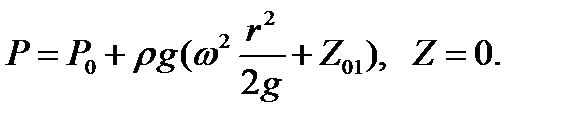

2)Z₀₂=0: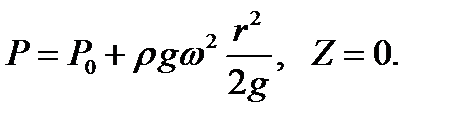

3) Z₀₃< 0: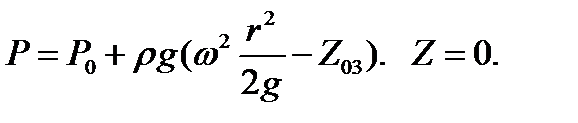

Для первого варианта. Выражение для силы dF, действующей на элементарную кольцевую площадку 2πrdr

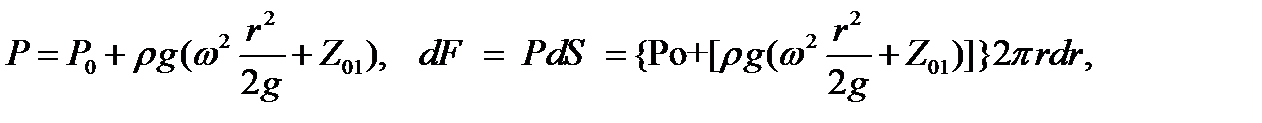
а затем выполняем интегрирование в требуемых пределах.

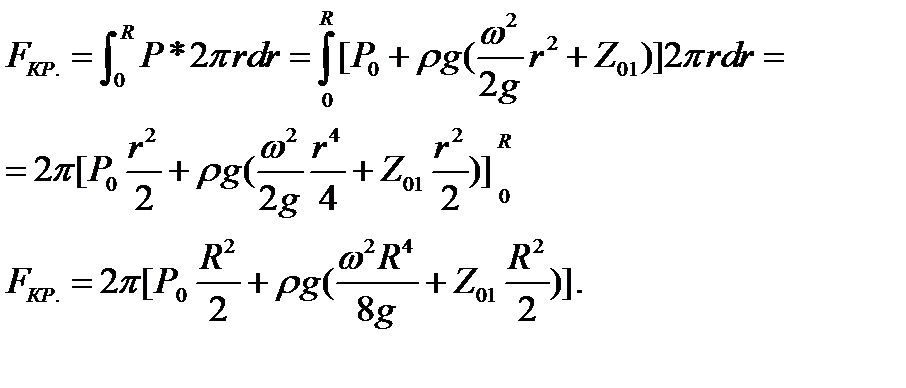
Также выполняется интегрирование во втором и третьем случае.

Определение сил давления жидкости на вертикальную стенку, сначала находим элементарную силу давления на кольцо, меняется высота, радиус остается неизменным

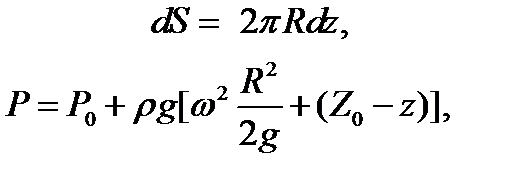
Сила, действующая на всю стенку равна

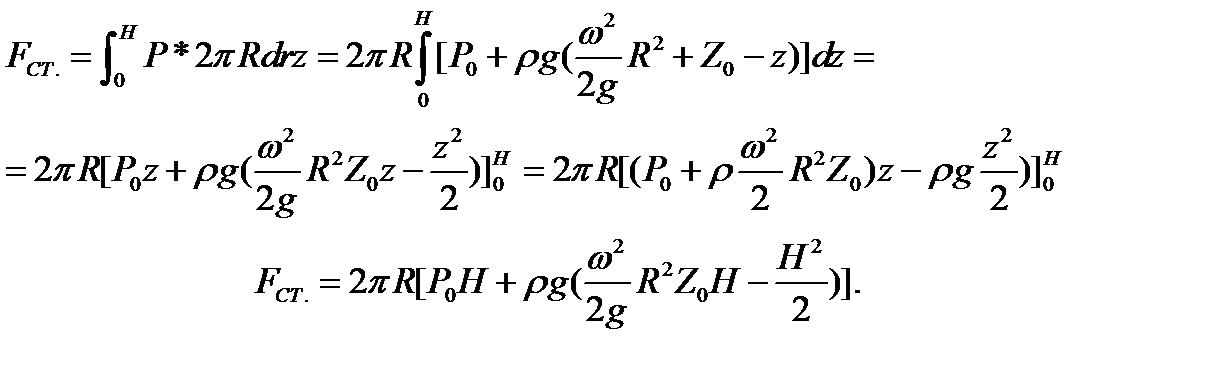
ГИДРОСТАТИКА-3

Вопросы к лекции:

Относительный покой жидкости .Прямолинейное движение с постоянным ускорением. Определение давления в любой точке.

Прямолинейное движение с постоянным ускорением. Определение положения свободной поверхности при движении сосуда.