Некоторые замечательные пределы

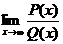, где P(x) = a₀xⁿ + a₁x^n-1 +…+a_n,

Q(x) = b₀x^m + b₁x_m-1 +…+b_m - многочлены.

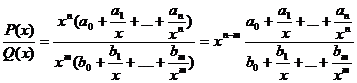
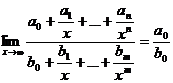
Итого: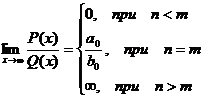

Первый замечательный предел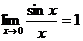

Второй замечательный предел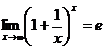

Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.

Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:

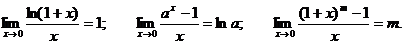
Пример. Найти предел.

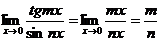
Пример. Найти предел.

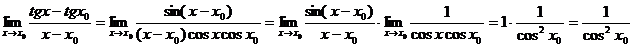
Пример. Найти предел.

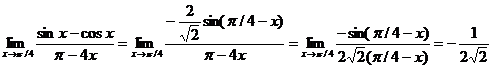
Пример. Найти предел.

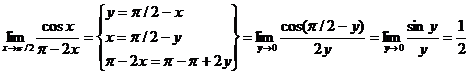
Пример. Найти предел.

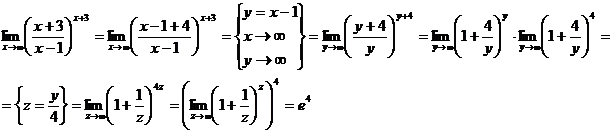
Пример. Найти предел .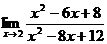

Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.

x² – 6x + 8 = 0; x² – 8x + 12 = 0;

D = 36 – 32 = 4; D = 64 – 48 = 16;

x₁ = (6 + 2)/2 = 4; x₁ = (8 + 4)/2 = 6;

x₂ = (6 – 2)/2 = 2 ; x₂ = (8 – 4)/2 = 2;

Тогда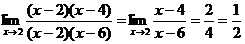

Пример. Найти предел.

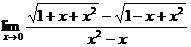домножим числитель и знаменатель дроби на сопряженное выражение: =

= .

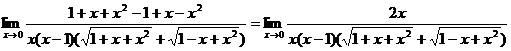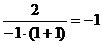Пример. Найти предел.

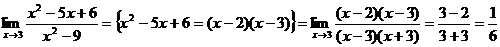
Пример. Найти предел .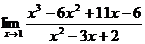

Разложим числитель и знаменатель на множители.

x² – 3x + 2 = (x – 1)(x – 2)

x³ – 6x² + 11x – 6 = (x – 1)(x – 2)(x – 3), т.к.

x³ – 6x² + 11x – 6 x - 1

x³ – x² x² – 5x + 6

- 5x² + 11x

- 5x² + 5x

6x - 6

6x - 6 0

x² – 5x + 6 = (x – 2)(x – 3)

Тогда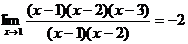

Пример. Найти предел.

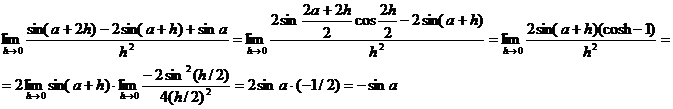
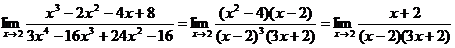- не определен, т.к. при стремлении х к 2 имеют место различные односторонние пределы -∞ и +∞.

Комплексные числа

Определение. Комплексным числом zназывается выражение 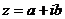, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:

При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).

Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.

Определение. Числа 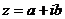и 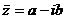называются комплексно – сопряженными.

Определение. Два комплексных числа 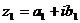и 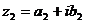называются равными, если соответственно равны их действительные и мнимые части:

Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.

Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.

Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.

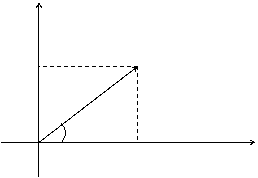у

A(a, b)

r b

j

0 a x

Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые.

С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.