Математические модели объектов диагноза.

Формализация методов построения алгоритмов диагноза некоторого объекта предполагает наличие формального описания объекта и его поведения в исправном и неисправных состояниях. Такое формальное описание (в аналитической, табличной, векторной, графической или другой форме) будем называть математической моделью объекта диагноза. Математическая модель объекта диагноза может быть задана в явном или неявном виде.

Явнаямодель объекта диагноза представляет собой совокупность формальных описаний исправного объекта и всех (точнее, каждой из рассматриваемых) его неисправных модификаций. Для удобства обработки все указанные описания желательно иметь в одной и той же форме. Неявнаямодель объекта диагноза содержит какое-либо одно формальное описание объекта, математические модели его физических неисправностей и правила получения по этим данным всех других интересующих нас описаний. Чаще всего заданной является математическая модель исправного объекта, по которой можно построить модели его неисправных модификаций.

Общие требования к моделям исправного объекта и его неисправных модификаций, а также к моделям неисправностей состоят в том, что они должны с требуемой точностью описывать представляемые ими объекты и их неисправности. В неявных моделях объектов диагноза модели неисправностей, кроме того, должны удовлетворять требованию удобства их «сопряжения» с имеющимся описанием объекта и тем самым обеспечить достаточно простые правила получения других описаний объекта.

Исправный или неисправный объект может быть представлен как динамическая система, состояниекоторой в каждый момент времени tопределяется значениями входных, внутренних и выходных координат (параметров). Частным является случай, когда состояние объекта не зависит от времени.

Обратим внимание на то, что термин «состояние объекта» (как динамической системы), обозначающий совокупность значений параметров объекта в определенный момент времени, не следует смешивать с термином «техническое состояние объекта», обозначающим наличие или отсутствие неисправности в объекте.

Объекты диагноза разделим на классы. Объекты, все координаты которых могут принимать значения из континуальных множеств значений, отнесем к классу непрерывных объектов. К классу дискретных объектовпричислим объекты диагноза, значения всех координат которых задаются на конечных множествах, а время отсчитывается дискретно. Если значения части координат объекта заданы на континуальных, а значения других - на конечных множествах, то объект является гибридным

Объекты будем называть комбинационными,или объектами без памяти, если значения их выходных координат однозначно определяются только значениями их входных координат. Последовательностными, или объектами с памятью, являются объекты, у которых наблюдается зависимость значений их выходных координат не только от значений входных координат, но и от времени.

Приведем примеры простых объектов разных классов: резистивная электрическая сеть - непрерывный объект без памяти, аналоговая система регулирования с обратными связями - непрерывный объект с памятью, диодный дешифратор двоичных сигналов - дискретный комбинационный объект, двоичный счетчик - дискретный объект с памятью, аналого-цифровой преобразователь - гибридный объект.

Часто входные и внутренние координаты объекта называют входнымии соответственно внутренними переменными, а выходные координаты - выходными функциями. Мы также будем пользоваться этими названиями. Заметим, что входные переменные и выходные функции могут быть сопоставлены как основным, так и дополнительным входам и соответственно выводам объекта.

Обозначим символом Xn-мерный вектор, компонентами которого являются значения пвходных переменных x₁, x₂, …, x_n.Аналогично Yявляется m-мерным вектором значений mвнутренних переменных у₁, у₂, ..., у_т, aZ-k-мерным вектором значений kвыходных функций z₁, z₂, …, z_k. Запись

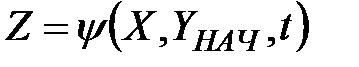(2.1.)

будем рассматривать как некоторую аналитическую, векторную, графическую, табличную или другую формы представления системы передаточных функций исправного объекта диагноза, отражающих зависимость реализуемых объектом выходных функций Zот его входных переменных X, начального значения Y_нач внутренних переменных и от времени t. Система (2.1) является математической моделью исправного объекта.

Выделим для рассмотрения конечное множество возможных неисправностей объекта. Принято различать одиночные и кратные неисправности. Под одиночнойпонимается неисправность, принимаемая в качестве элементарной, т.е. такой, которая не может быть представлена (или не подлежит представлению) совокупностью нескольких других, более «мелких» неисправностей.Кратнаянеисправность является совокупностью одновременно существующих двух или большего числа одиночных неисправностей. Символом Sбудем обозначать множество всех рассматриваемых (не обязательно всех возможных) одиночных и кратных неисправностей объекта, а символомО - множество его одиночных неисправностей. Очевидно, 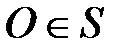. 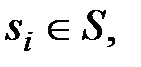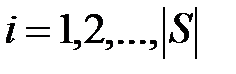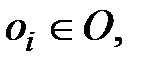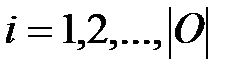Будем говорить, что при наличии в объекте неисправности или он находится в i-неисправном состоянии или является i-неисправным.

Объект диагноза, находящийся в i-неисправном состоянии, реализует систему передаточных функций

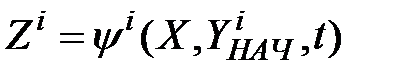(2.2.)

представленных в той же форме, что и передаточные функции (2.1). Заметим, что начальное значение Y_нач внутренних переменных i-неисправного объекта может не совпадать с их начальным значением Y_нач в исправном объекте. Система (2.2) для фиксированного iявляется математической моделью i-неисправного объекта.

Система (2.1)и совокупность систем (2.2)для всех 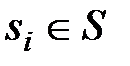образуют явную модель объекта диагноза. Будем такую модель обозначать записью .

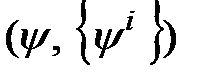Часто, как отмечалось выше, в явном виде задается только модель исправного объекта, т.е. зависимость (2.1), а поведение объекта в i-неисправных состояниях представляется косвенно через множество S возможных неисправностей. В этом случае неявную модель объекта диагноза образуют: зависимость (2.1), множество S возможных неисправностей объекта (представленных их математическими моделями) и, наконец, способ вычисления зависимостей (2.2) по зависимости (2.1) для любой неисправности s_i. Такую неявную модель объекта диагноза будем обозначать записью .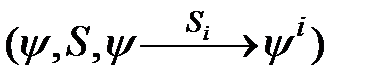

Если математические модели неисправностей известны для всех 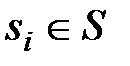, то преобразованием 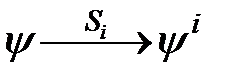можно получить все зависимости (2.2) и тем самым от модели 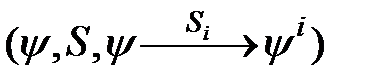перейти к явной модели 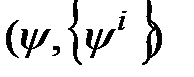. Если же математические модели некоторых или даже всех неисправностей из множества S неизвестны, то зависимости (2.2) могут быть получены в результате физического эксперимента непосредственно над объектом диагноза при наличиив нем соответствующих неисправностей. Модификацией этого подхода является использование при эксперименте не самого объекта, а некоторой его физической модели.

Основным понятием, используемым при решении задач построения и реализации алгоритмов диагноза, является элементарная проверка объекта. Рассмотрим вопросы задания моделей объектов диагноза в терминах элементарных проверок объекта и их результатов.

Обозначим символом П множество всех допустимых элементарных проверок 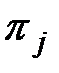, 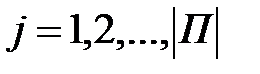объекта, т.е. таких его проверок, которые физически осуществимы в конкретных условиях проведения процесса диагноза. Каждая элементарная проверка, по определению, характеризуется значением воздействия, подаваемого (поступающего) на объект при реализации элементарной проверки, и ответом объекта на это воздействие. Значение 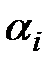воздействия в элементарной проверке 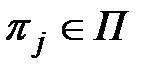определяется составом входных переменных и последовательностью во времени tих значений X_j, а также начальным значением Y_iнач внутренних переменных. Ответ объекта в элементарной проверке 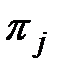характеризуется составом 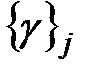контрольных точек и значением (результатом элементарной проверки) 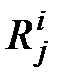, зависящим от технического состояния объекта (отсутствие индекса iсоответствует исправному объекту).

Таким образом, результат 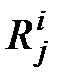элементарной проверки представляется в общем случае последовательностью 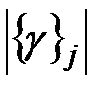- мерных векторов и является функцией значения 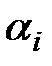воздействия:

.

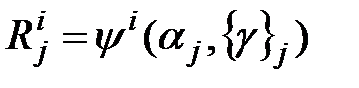Вместо этой записи условимся применять более короткую:

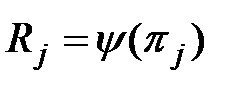- для исправного объекта (2.3)

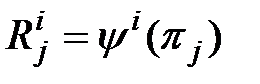- для i-неисправных объектов. (2.4)

Описанию фактического поведения объекта соответствует запись

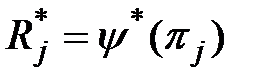(2.5)

Связь между моделями типа (2.1),(2.2) и типа (2.3),(2.4)заключается в том, что последние могут быть получены путем подстановки в правые части (2.1) и (2.2)значений X_j,, Y_{нач ё}, t(для каждой элементарной проверки 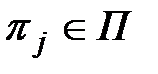) и последующего вычисления значений тех компонент векторов ZиZⁱ, которые сопоставлены контрольным точкам из множеств .

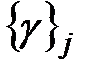Явную модель объекта диагноза, когда зависимости (2.1 - 2.5) заданы для всех 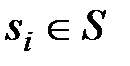, будем обозначать, как и прежде, записью 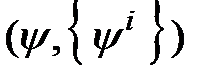. Неявная модель объекта диагноза в данном случае предполагает заданными модель 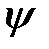исправного объекта, множество S неисправностей, а также множество П допустимых элементарных проверок и поэтому представляется записью