Лекция 14. «Системы массового обслуживания с восстановлением»

План лекции:

Система с восстановлением без резервирования

Однократное общее нагруженное резервирование с восстановлением

Система с восстановлением без резервирования

В тех случаях, когда после отказа устройство не выбрасывается, а ремонтируется, СМО относят к группе систем с восстановлением.

Обозначим через интенсивность отказов устройства, через – интенсивность восстановления. Величина , по-существу, представляет собой среднее время ремонта (восстановления) устройства.

Система с восстановлением без резервирования может находиться в двух состояниях (рис. 14.1):

– устройство исправно, работает, ремонтная бригада свободна, отдыхает,

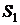– устройство отказало, неисправно, бригада ремонтирует отказавшее устройство. По окончании ремонта система перейдёт в состояние с интенсивностью, определяемой интенсивностью восстановления.

Вероятность нахождения системы в состоянии есть вероятность безотказной работы системы в целом, то есть _. Вероятность нахождения системы в состоянии 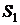представляет собой вероятность отказа всей системы, иначе .

Рис. 14.1. Граф состояний системы без резервирования с восстановлением

Система уравнений, описывающая данный граф состояний, включает в себя два уравнения:

Преобразуем оба уравнения по Лапласу

Решая совместно, выразим изображения вероятностей состояний друг через друга. Из второго уравнения в системе (14.2) получаем

Подставляя в первое уравнение, имеем выражение

Отсюда

Используя обратное преобразование Лапласа, получаем выражения

и

Следовательно, надёжность системы без резервирования с восстановлением, уменьшаясь от единицы при , стремится с увеличением времени к постоянной величине – рис. 14.2.

Рис. 14.2. Зависимости надёжности и вероятности отказа от нормированного времени системы без резервирования с восста­новлением

Характерной особенностью СМО, в которых возможен переход из любого состояния в любое другое, является наличие установившегося режима, когда при достаточно большом времени вероятности всех состояний становятся постоянными. В установившемся режиме дифференциальные уравнения академика Колмогорова превращаются в алгебраические, так как . Поэтому в тех случаях, когда интерес представляют только установившиеся значения вероятностей состояний, составляют систему алгебраических уравнений, решение которой проще, чем системы дифференциальных уравнений.

Для системы без резервирования с восстановлением уравнения (14.1) в установившемся режиме преобразуются в

решение которых позволяет сразу найти формулы

к которым стремятся выражения (14.5), так как экспоненциальные множители в них стремятся к нулю с увеличением времени.

Полученные результаты можно трактовать либо как то, что через достаточно большой промежуток времени после начала работы вероятность безотказной работы описывает величину среднего относительного времени нахождения системы в исправном состоянии, либо как то, что для множества систем их отно­сительное количество будет в среднем исправно.

Чтобы повысить надёжность работы системы, надо или уменьшать интенсивность отказов, или увеличивать интенсивность восстановления, то есть уменьшать среднюю продолжительность ремонта, или делать и то и другое одновременно. Это вполне согласуется "со здравым смыслом".