С общим двукратным ненагруженным резервированием

Обозначения состояний системы	Вероятность нахождения в данном состояний	Состояния
системы в целом	основного устройства	первого резервного устройства	второго резервного устройства
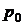		Исправна	Исправно, работает	Исправно, выключено	Исправно, выключено
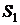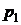		Исправна	Неисправно	Исправно, работает	Исправно, выключено
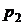		Исправна	Неисправно	Неисправно	Исправно, работает
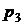		Неисправна	Неисправно	Неисправно	Неисправно

Поэтому вероятность безотказной работы системы с двукратным общим ненагруженным резервированием без восстановления есть сумма вероятностей нахождения системы в любом из состояний , 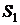и , то есть

.

Составим уравнения академика Колмогорова для этой системы:

Уравнение совпадает с уравнением . Поэтому в операторной форме имеем выражение (11.16)

а решение этого уравнения совпадает с формулой (11.17):

Получим изображение уравнения :

Учитывая, что , получаем выражение аналогичное (11.18)

Возможны два варианта организации резервирования: а) основное и резервное устройства разные по надёжности и б) они одинаковые.

Пусть имеет место вариант "а)", при котором выполняется условие . Это соответствует случаю простых корней: . Поэтому решение уравнения (12.2 b) будет иметь вид

что совпадает с формулой (11.19).

Если основное и резервное устройства одинаковые, то выполняется равенство (вариант"б)") и формула (12.6) примет вид

Обратное преобразование Лапласа позволяет найти вероятность , выражение которой совпадает с формулой (11.22):

Преобразуя уравнение по Лапласу и приводя подобные члены с учётом того, что , получим

Если выполняются условия , то, используя формулу (12. 6), получим

Это случай простых корней. Поэтому

Отсюда после алгебраических преобразований получаем формулу вероятности безотказной работы системы при двукратном ненагруженном резервировании без восстановления для случая, когда основное и резервные устройства разные, то есть выполняются условия :

Если выполняются условия , то используя формулу (12. 8), получим

Это случай кратных корней: – кратность 2, – кратность 1. Поэтому

Поэтому искомая вероятность безотказной работы системы (12.1) путём сложения величин (12.4), (12.9) и (12.15) можно рассчитать по формуле

Если выполняются условия , то

Обратное преобразование Лапласа позволяет получить выражение

Поэтому искомая вероятность и окончательно

Если выполняются условия , то имеет место один корень с кратностью 3:

Поэтому решением будет формула

Для этого случая имеем выражение и конкретно

На рис. 12.2 приведены зависимости вероятности безотказной работы и выигрыша по надёжности системы с общим двукратным ненагруженным резервированием от нормированного времени .

Рис. 12.2. Вероятность безотказной работы (а) и выигрыш по надёжности (б) для системы с общим двукратным ненагруженным резервированием

Из рисунка следует, что с ростом интенсивности отказов резервных элементов выигрыш по надёжности уменьшается медленно. Однако на уровне 0,9 при интенсивностях отказов, связанных соотношениями , выигрыш по времени составляет 5,5 раза, в то время как при соотношениях он превышает 10.