Учёт надёжности переключающих элементов
Рассмотрим влияние переключающих устройств на надёжность системы с однократным общим нагруженным резервированием.
Обозначим вероятность безотказной работы основного устройства через 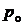 , резервного – через
, резервного – через 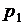 . Согласно формуле (6.4) вероятность безотказной работы такого резервирования определяется выражением
. Согласно формуле (6.4) вероятность безотказной работы такого резервирования определяется выражением
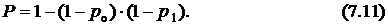
Устройство коммутации должно содержать блок определения неисправности основного канала (БОН). При обнаружении несоответствия параметров сигнала требуемым значениям блок должен переключить каналы и подключить на выход системы резервное устройство.
В простейшем случае использования электромагнитного реле для коммутации в каждый канал будет включено по контактной паре с одинаковой надёжностью 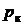 для основного и резервного каналов.
для основного и резервного каналов.
Блок определения неисправности основного канала и обмотку реле следует считать включёнными в общий канал, так как отказ в работе любого из них приводит к отказу в работе всей системы (рис. 7.3).

Рис. 7.3. Схема однократного общего нагруженного резервирования с учётом переключающих устройств
Следовательно, для расчёта вероятности безотказной работы системы с учётом переключающих устройств можно использовать формулу (7.10) расчёта надёжности системы со смешанным резервированием. Конкретно получаем
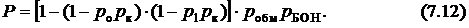
Как и следовало ожидать, надёжность уменьшилась, так как увеличилось число элементов в системе.
Резервирование целесообразно применять, если увеличение надёжности превышает её уменьшение из-за введения блока определения неисправности и коммутирующего устройства.
Лекция 8. «Оптимизация резервирования»
План лекции:
Метод множителей Лагранжа
Оптимизация резервирования
Метод множителей Лагранжа
При резервировании возникает задача обеспечения требуемой вероятности безотказной работы системы при минимальных затратах, то есть задача оптимизации, которую удобно решать методом множителей Лагранжа.
Метод множителей Лагранжа применяют для нахождения экстремума функции нескольких переменных, заданной аналитически при наличии ограничений в форме равенств.
Математически задача формулируется следующим образом.
Дано уравнение целевой функции  переменных
переменных 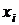
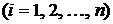

и  уравнений-ограничений (уравнений связи) в виде равенств
уравнений-ограничений (уравнений связи) в виде равенств
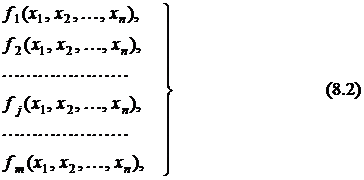
причём 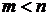 .
.
Требуется найти такие значения переменных 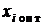 , которые бы обеспечивали получение экстремума целевой функции.
, которые бы обеспечивали получение экстремума целевой функции.
Классический подход к решению предусматривает выбор 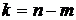 переменных в качестве независимых и использование уравнений связи для выражения остальных
переменных в качестве независимых и использование уравнений связи для выражения остальных  переменных через
переменных через 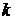 независимых. Далее следует заменить
независимых. Далее следует заменить  зависимых переменных в уравнении целевой функции через независимые и искать экстремум целевой функции теперь уже как функции
зависимых переменных в уравнении целевой функции через независимые и искать экстремум целевой функции теперь уже как функции 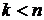 переменных.
переменных.
Однако этот путь решения является трудоёмким и неэффективным, так как имеется только одно уравнение с 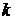 неизвестными.
неизвестными.
Лагранж (французский математик XVIII века) предложил ввести ещё  новых переменных
новых переменных 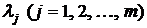 и, используя их в качестве неопределённых множителей, сформировать функцию вида
и, используя их в качестве неопределённых множителей, сформировать функцию вида
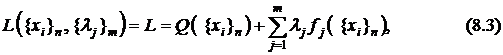
впоследствии названную функцией Лагранжа.
Фигурные скобки обозначают краткую запись множества переменных, мощность которого указана внешним индексом.
Известно, что в точке экстремума полный дифференциал функции обращается в нуль, то есть

где 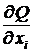 – частная производная.
– частная производная.
Дифференцируя уравнения связи (8.2), получим в той же точке  равенств
равенств
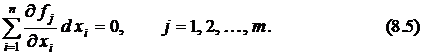
Введём новые переменные 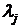 , умножим уравнения (8.5) на эти пока неопределённые множители и сложим их почленно с уравнением (8.4)
, умножим уравнения (8.5) на эти пока неопределённые множители и сложим их почленно с уравнением (8.4)
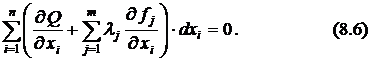
Определим  множителей
множителей 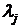 из условия, чтобы коэффициенты при
из условия, чтобы коэффициенты при  дифференциалах
дифференциалах 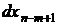 ,
, 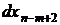 ,
, 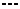 зависимых переменных были равны нулю, то есть определим
зависимых переменных были равны нулю, то есть определим 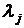 из
из  равенств
равенств
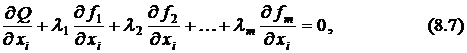
где  .
.
Поэтому в левой части уравнения (8.6) останутся только члены, содержащие дифференциалы независимых переменных, то есть
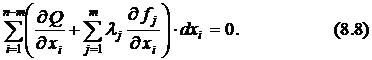
Так как дифференциалы независимых переменных есть произвольные величины, то из этого определения и последнего уравнения вытекает, что все коэффициенты в (8.8) должны быть равны нулю. Таким образом, получаем в точке экстремума систему  уравнений вида
уравнений вида
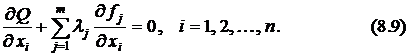
Вместе с системой уравнений связи (8.2) имеем систему 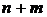 уравнений для нахождения
уравнений для нахождения 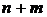 переменных (
переменных (  переменных вида
переменных вида 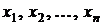 и
и  переменных вида
переменных вида 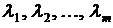 ).
).
Решение системы 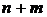 уравнений оказывается проще, чем решение уравнения (8.1) после замены зависимых переменных.
уравнений оказывается проще, чем решение уравнения (8.1) после замены зависимых переменных.
Таким образом, в соответствии с методом множителей Лагранжа алгоритм поиска экстремума функции нескольких переменных при наличии ограничений можно представить в виде:
1) формирование функции Лагранжа
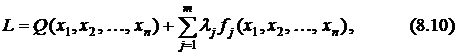
2) взятие первых частных производных по всем переменным 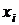 и приравнивание их нулю:
и приравнивание их нулю:
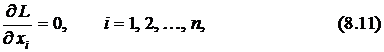
что совпадает с уравнениями (8.9),
3) дополнение полученных  уравнений системой из
уравнений системой из  уравнений связи (8.2),
уравнений связи (8.2),
4) решение систем уравнений (8.2) и (8.11) как единой системы из 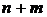 уравнений. Найденные в результате решения значения переменных
уравнений. Найденные в результате решения значения переменных 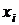 соответствуют точкам экстремумов,
соответствуют точкам экстремумов,
5) выбор глобального экстремума в точке 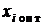 .
.
Оптимизация резервирования
Рассмотрим применение метода множителей Лагранжа для оптимизации радиоэлектронного устройства путём раздельного нагруженного резервирования.
Задачу формулируют следующим образом. Разработанная конструкция РЭУ, состоящая из  блоков (или элементов), имеет недостаточную надёжность:
блоков (или элементов), имеет недостаточную надёжность: 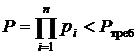 . Здесь
. Здесь 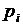 – вероятность безотказной работы блока номера
– вероятность безотказной работы блока номера 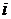 . Необходимо обеспечить требуемую надёжность
. Необходимо обеспечить требуемую надёжность 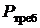 РЭУ путём резервирования блоков (или элементов) при минимальных затратах.
РЭУ путём резервирования блоков (или элементов) при минимальных затратах.
Эквивалентная схема раздельного нагруженного резервирования (рис. 8.1) совпадает с рис. 7.1, а.
Целевой функцией является стоимость системы с резервированием:
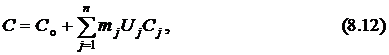
где 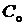 – стоимость основного устройства,
– стоимость основного устройства, 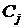 – стоимость резервного блока номера
– стоимость резервного блока номера 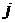 ,
, 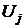 – коэффициент увеличения стоимости системы за счёт установки блока
– коэффициент увеличения стоимости системы за счёт установки блока 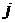 , учитывающий увеличение объёма, массы и других показателей,
, учитывающий увеличение объёма, массы и других показателей, 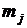 – кратность резервирования блока
– кратность резервирования блока 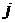 .
.
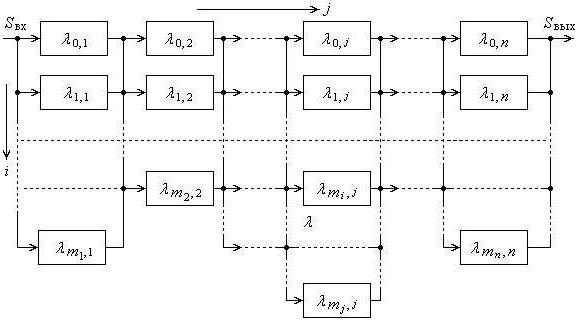
Рис. 8.1. Раздельное нагруженное резервирование
Неизвестными переменными являются кратности резервирования 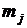 . Для простоты будем считать, что основной
. Для простоты будем считать, что основной 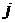 -й и резервирующие его блоки одинаковые. Поэтому вероятность безотказной работы можно рассчитать по формуле
-й и резервирующие его блоки одинаковые. Поэтому вероятность безотказной работы можно рассчитать по формуле 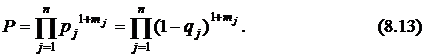
Как правило, вероятность отказа блока (узла, элемента) 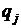 мала и выражение (8.13) можно упростить, раскрывая скобки и пренебрегая слагаемыми второго
мала и выражение (8.13) можно упростить, раскрывая скобки и пренебрегая слагаемыми второго 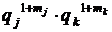 и более высокого порядка в силу их малости:
и более высокого порядка в силу их малости:
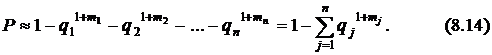
Поэтому уравнение связи можно записать как
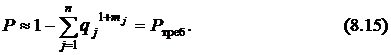
Оно является единственным уравнением-ограничением, то есть 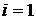 , и в стандартной форме записи (8.2) выглядит в виде
, и в стандартной форме записи (8.2) выглядит в виде
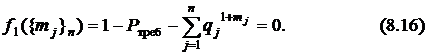
Сформируем функцию Лагранжа
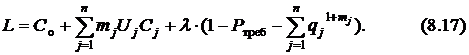
Возьмём частные производные этой функции по 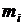 и приравняем их нулю:
и приравняем их нулю: 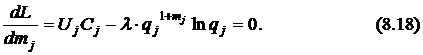
Выражая неизвестные 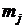 через
через 

и подставляя их в формулу (8.15)
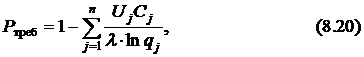
находим множитель Лагранжа

Теперь заменим  в формуле (8.19)
в формуле (8.19)
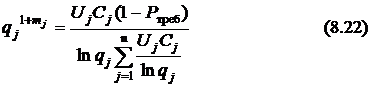
и найдём искомые переменные
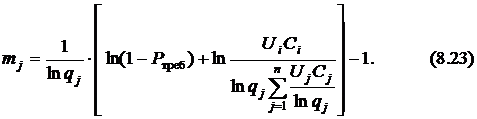
Задача решена.
Однако значения кратности 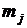 по формуле (8.23) почти всегда получаются дробными, а они могут быть только целыми числами. Поэтому вначале найденные значения
по формуле (8.23) почти всегда получаются дробными, а они могут быть только целыми числами. Поэтому вначале найденные значения 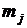 округляют по обычным правилам до целых. Затем увеличивают на единицу те из округлённых значений
округляют по обычным правилам до целых. Затем увеличивают на единицу те из округлённых значений 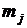 , у которых дробная часть была меньше 0,5, а вероятность безотказной работы этого блока номера удовлетворяла условию
, у которых дробная часть была меньше 0,5, а вероятность безотказной работы этого блока номера удовлетворяла условию 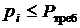 . Далее рассчитывают при найденных кратностях получающуюся вероятность безотказной работы по формулам (7.4) или (8.13) и сравнивают с требуемой
. Далее рассчитывают при найденных кратностях получающуюся вероятность безотказной работы по формулам (7.4) или (8.13) и сравнивают с требуемой 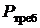 .
.
Если полученная надёжность равна или превышает 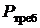 , то рассчитывают по формуле (8.12) стоимость, которая является минимальной по сравнению с другими вариантами кратности резервирования.
, то рассчитывают по формуле (8.12) стоимость, которая является минимальной по сравнению с другими вариантами кратности резервирования.
Если полученная надёжность меньше 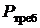 , то последовательно, начиная с блоков, у которых произведение
, то последовательно, начиная с блоков, у которых произведение  минимально, увеличивают соответствующее значение
минимально, увеличивают соответствующее значение 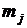 на единицу и рассчитывают вероятность безотказной работы. Первый вариант, для которого будет выполнено условие
на единицу и рассчитывают вероятность безотказной работы. Первый вариант, для которого будет выполнено условие 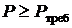 , обеспечит оптимальное резервирование. Необходимость последовательной проверки указанного условия объясняется тем, что уравнение связи (8.15) фактически является неравенством вида
, обеспечит оптимальное резервирование. Необходимость последовательной проверки указанного условия объясняется тем, что уравнение связи (8.15) фактически является неравенством вида  , а по методу Лагранжа должно быть строгое равенство.
, а по методу Лагранжа должно быть строгое равенство.
Пример.
а) Дано:  =3,
=3, 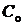 = 4400 руб.,
= 4400 руб., 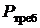 = 0,98,
= 0,98,
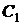 = 1800 руб.,
= 1800 руб., 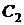 = 1200 руб.,
= 1200 руб., 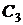 = 1400 руб.,
= 1400 руб.,
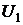 = 1,3,
= 1,3, 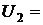 1,35,
1,35, 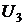 =1,15,
=1,15,
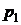 = 0,95,
= 0,95,  0,99,
0,99, 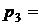 0,97.
0,97.
Найти такие кратности резервирования блоков, которые бы обеспечили требуемую надёжность при минимальных дополнительных затратах.
Решение:
1) находим 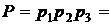 0,9123,
0,9123, 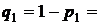 0,05,
0,05, 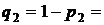 0,01,
0,01, 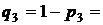 0,03,
0,03,
2) рассчитываем по формуле (8.23) 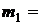 0,549,
0,549, 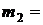 0,216,
0,216, 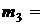 0,429,
0,429,
3) округляем 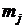 по обычным правилам
по обычным правилам 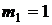 ,
, 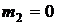 ,
, 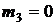 ,
,
4) увеличиваем на единицу 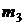 , так как
, так как 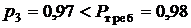 , то есть принимаем
, то есть принимаем  ,
,
5) проверяем получившуюся надёжность
 0,9975.0,99.0,9991= 0,9866
0,9975.0,99.0,9991= 0,9866 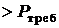 ,
,
6) рассчитываем дополнительные затраты на установку резервных блоков: 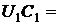 1,3*1800 = 2340 руб.,
1,3*1800 = 2340 руб., 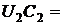 1,35*1200 = 1620 руб.,
1,35*1200 = 1620 руб., 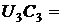 =1,15*1400 = 1610 руб.,
=1,15*1400 = 1610 руб.,
7) рассчитываем стоимость устройства с резервными блоками
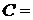 4400 + 2340 + 1610 = 8350 руб.
4400 + 2340 + 1610 = 8350 руб.
б) Дано:  =3,
=3, 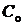 = 4400 руб.,
= 4400 руб., 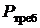 = 0,98,
= 0,98,
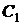 = 1800 руб.,
= 1800 руб., 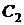 = 1200 руб.,
= 1200 руб., 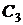 = 1400 руб.,
= 1400 руб.,
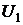 = 1,3,
= 1,3, 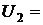 1,35,
1,35, 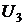 =1,15,
=1,15,
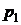 = 0,95,
= 0,95,  0,985,
0,985, 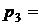 0,997.
0,997.
Найти такие кратности резервирования блоков, которые бы обеспечили требуемую надёжность при минимальных дополнительных затратах.
Решение:
1) находим 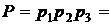 0,926,
0,926, 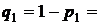 0,05,
0,05, 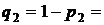 0,015,
0,015, 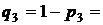 0,003,
0,003,
2) рассчитываем по формуле (8.23) 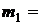 0,527,
0,527, 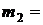 0,258,
0,258, 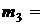 0,168,
0,168,
3) округляем 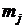 по обычным правилам
по обычным правилам 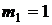 ,
, 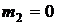 ,
, 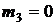 ,
,
4) проверяем получившуюся надёжность
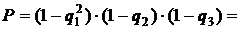 0,9975.0,985.0,997
0,9975.0,985.0,997 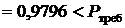 ,
,
5) рассчитываем дополнительные затраты на установку резервных блоков: 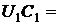 1,3*1800 = 2340 руб.,
1,3*1800 = 2340 руб., 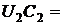 1,35*1200 = 1620 руб.,
1,35*1200 = 1620 руб., 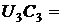 =1,15*1400 = 1610 руб.,
=1,15*1400 = 1610 руб.,
6) увеличиваем на 1 кратность блока с минимальным произведением 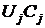 . Это третий блок. Поэтому принимаем
. Это третий блок. Поэтому принимаем  ,
,
7) проверяем получившуюся надёжность
 0,9975.0,985.0,999991= 0,9825
0,9975.0,985.0,999991= 0,9825 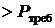 ,
,
6) рассчитываем стоимость устройства с резервными блоками
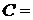 4400 + 2340 + 1610 = 8350 руб.
4400 + 2340 + 1610 = 8350 руб.
Следовательно, для получения требуемой надёжности системы экономически более выгодным оказалось резервировать третий более надёжный блок, чем второй.
Лекция 9. «Основные понятия теории массового обслуживания»
План лекции:
Основные понятия теории массового обслуживания
Потоки заявок
