Числовые характеристики вероятности безотказной работы

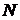	0,10	0,20	0,30	0,40	0,50
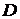	0,09	0,180	0,270	0,36	0,450	0,900
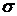	0,30	0,424	0,520	0,60	0,671	0,949		9,487
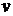		2,121	1,732	1,50	1,342	0,949	0,3	0,095

Закон Пуассона

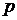Распределение Пуассона является предельным случаем для биномиального, когда число опытов неограниченно увеличивается, а вероятность появления опыта неограниченно уменьшается, но так, что их произведение 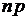в пределе стремится к постоянной величине, т.е. 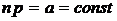[2]. Поэтому вероятность появления ровно событий должна быть описана формулой

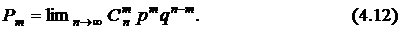
Учитывая формулу (4.2) и то, что 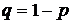, , 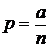преобразуем выражение (4.12) к виду

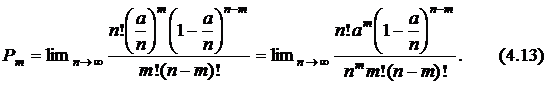
Сокращая 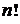в числителе с 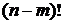в знаменателе, получим в числителе многочлен вида 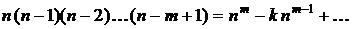, который в пределе с множителем 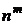в знаменателе, стремится к единице. Поэтому будем иметь промежуточное выражение

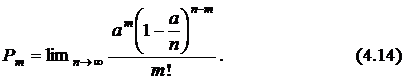
Домножим и разделим выражение (4.14) на 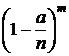. В итоге в числителе получим множитель .

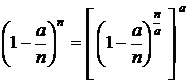Обозначая в нём 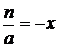, получим стандартное выражение 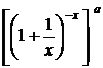, пределом которого при , стремящемся к бесконечности, является показательная функция 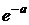[10, с.294].

Пределом выражения 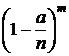в знаменателе при бесконечном и постоянном является единица.

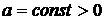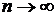Следовательно, предельное значение формулы (4.14) при и равно

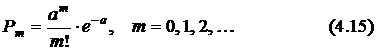
Оно представляет собой математическую формулировку распределения случайной величины по закону Пуассона.

Закон Пуассона является частным случаем биномиального. Однако он находит достаточно широкое применение, так как существует ряд процессов, в которых для расчёта можно использовать только распределение Пуассона, а биномиальное – нет [4].

Биномиальное распределение можно применять для любой величины вероятности появления события 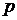, а распределение Пуассона – только для малого 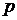(практически для 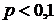). Для биномиального распределения должно выполняться услови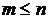е , где конечно и должно быть известно, а для распределения Пуассона может принимать любое целое значение от нуля до бесконечности.

Так как распределение Пуассона можно приближённо применять вместо биномиального, когда возможное число опытов велико, а вероятность появления каждого из них очень мала, то иногда это распределение называют "законом редких событий".

Основными числовыми характеристиками распределения Пуассона являются:

– математическое ожидание

– дисперсия

– среднеквадратическое отклонение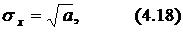

– коэффициент вариации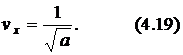

В отличие от биномиального распределения в этом случае числовые характеристики есть постоянные величины.

Характерной особенностью пуассоновского распределения является то, что его параметр 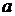равен одновременно математическому ожиданию и дисперсии.

Пример 4.2. Пусть имеется большое количество 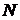одинаковых изделий с одинаковой интенсивностью отказов у каждого. Моменты появления отказов являются случайными событиями и представляют собой поток таких событий. Так как интенсивность отказов очень маленькая величина, то вероятность появления отказа тоже мала.

Поток событий, обладающий стационарностью, ординарностью и отсутствием последействия, называют простейшим или стационарным пуассоновским потоком.

Свойство стационарности означает, что вероятность попадания того или иного числа событий на участок времени длины 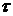не зависит от того, где на оси времени расположен этот участок, а зависит только от его длины 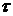. Отсюда следует, что среднее число событий, появляющихся в единицу времени, постоянно. Интенсивность отказов является интенсивностью потока отказов.

Свойство ординарности означает, что вероятность попадания на малый интервал времени двух или более событий пренебрежимо мала по сравнению с вероятностью попадания на него одного события.

Свойство отсутствия последействия означает, что вероятность попадания того или иного числа событий на заданный участок оси времени не зависит от того, сколько событий попало на любой другой не пересекающийся с ним участок. То есть термин "отсутствие последействия" означает, что будущее потока не зависит от его прошлого. Эта независимость сводится к тому, что события появляются на оси времени в силу случайных причин, индивидуальных для каждого из них.

Биномиальное распределение в случае ординарного потока без последействия стремится к пуассоновскому (4.15) с параметром 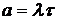, если 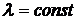и с параметром 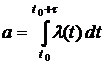, если интенсивность отказов зависит от времени.

Здесь 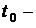начало интервала времени 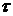. Параметр " 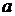" есть среднее число (математическое ожидание) отказов за интервал времени .

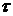Значения функции распределения Пуассона приведены в табл. 4.3 и представлены на рис. 4.2.

Таблица 4.3

Распределение Пуассона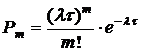

(вероятность безотказной работы изделий в интервале времени )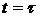

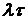	0,05	0,5	0,7
Р0	0,9512	0,6065	0,4966	0,3679	0,1353	0,0067
Р1	0,0476	0,3033	0,3476	0,3679	0,2707	0,0337
Р2	0,0012	0,0758	0,1217	0,1839	0,2707	0,0842
Р3	2.10–5	0,0126	0,0284	0,0613	0,1804	0,1404
Р4	2.10–7	0,0016	0,0050	0,0153	0,0902	0,1755
Р5	2.10–9	0,0002	0,0007	0,0031	0,0361	0,1755
Р6	2.10–11	1.10–5	8.10–5	0,0005	0,0120	0,1462

Рисунок 4.2 как и рисунок 4.1 представляет собой множество точек, расположенных на вертикальных линиях, соответствующих различным значениям вероятности безотказной работы устройств. А линии, соединяющие точки друг с другом проведены для удобства выделения групп точек, относящихся к одному семейству значений .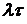

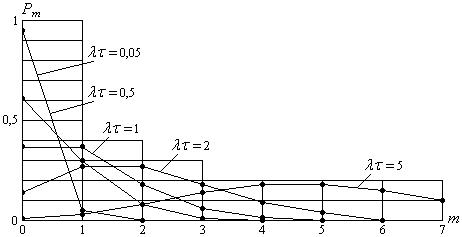
Рис. 4.2. Вероятность безотказной работы m устройств