Аналоговые и дискретные сигналы. Дискретная последовательность, частота дискретизации, нормирование, задержка последовательности, единичный импульс и скачок

Сигналом называют физический процесс, несущий в себе информацию. Математически сигналы описываются функциями времени; тип которых за­висит от типа сигнала. К основным типам сигналов относят: аналоговый, дискретный и цифровой.

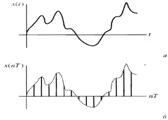
Аналоговым называют сигнал, непрерывный по времени и состоянию (рис. 1.3, а). Такой сигнал описывается непрерывной или кусочно-непрерывной функцией x(t), при этом и аргумент, и функция могут принимать любые зна­чения из некоторых интервалов 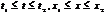соответственно.

Дискретным называют сигнал, дискретный по времени и непрерывный по состоянию (рис. 1.3,6) Такой сигнал описывается решетчатой функцией (последовательностью) х(пТ), п = 0,1, 2,..., которая определена только в дискретные моменты времени пТ и может принимать любые значения из некоторого интервала .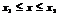

Интервал Т называют периодом дискретизации, а обратную величину — частотой дискретизации: 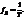Значения последовательности в моменты времени пТ называют отсчетами.

Цифровые сигналы в отличии от дискретных сигналов дискретны не только по времени, но и по состоянию, они могут принимать только конечное число значений из некоторого конечного интервала. Эти значения называются уровнями квантования, а соответствующие функции –квантованными.

При анализе дискретных сигналов удобно пользоваться нормированным временем 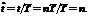Таким образом, номер отсчета n дискретного сигнала может интерпретироваться как нормированное время.

При изучении цифровых цепей в качестве испытательных воздействий чаще других используются два дискретных сигнала:

1) цифровой единичный импульс, который показан на рисунке 1,а и математически представлен соотношением

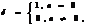где

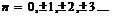
Задержанный цифровой единичный импульс описывается последовательностью

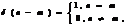
Этот сигнал, в отличие от незадержанного, равен единице при n=mи нулю при всех остальных значениях n.

2) цифровой единичный скачок, показан на рисунке 1,б и представлен математическим соотношением

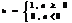,где

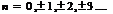
Задержанный цифровой единичный скачок описывается последовательностью

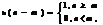
Этот сигнал, в отличие от незадержанного, равен единице при n≥m и нулю при всех остальных значениях n.

Рисунок 1

К типовым дискретным сигналам относятся также экспонента, гармонический сигнал и комплексный гармонический сигнал [1].

По теореме Котельникова максимальная частота аналогового сигнала f_max не должна превышать половины частоты дискретизации 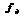, поэтому в частотной области все дискретные сигналы целесообразно рассматривать в диапазон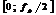е , где 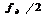- частота Найквиста. Это позволяет ввести понятие нормированной частоты 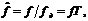где 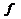- текущая частота. Тогда на частоте Найквиста 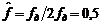. Таким образом дискретный сигнал можно рассматривать в основном частотном диапазоне .

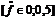Для нормированной круговой частоты 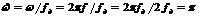, то есть основная полоса частот соответствует области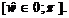

3 Прямое и обратное Z–преобразования. Свойства Z-преобразования

Полезным методом описания дискретных систем является z-преобразование, которое оказывается наглядной и удобной формой представления процессов, протекающих при цифровой обработке.

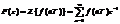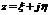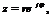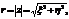Прямое z-преобразование определяет z-образ дискретной последовательности f(nT) следующим соотношением: (1.1). Дискретный сигнал f(nT) называется оригиналом, а функция F(z) - изображением (Z–образ). Аргумент z функции F(z) является комплексной величиной или в полярных координатах где а 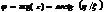. Комплексная функция F(z) определена лишь для тех значений z, при которых ряд (1.1) сходится. Условием сходимости ряда (1.1) является 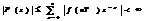. (1.2)

Удобным способом графического представления F(z) является изображение полюсов 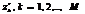и нулей 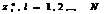функции в z-плоскости, называемое картой нулей и полюсов.

В таблице 1 представлены некоторые типовые последовательности и их прямые z-преобразования.

Т а б л и ц а 1

Последовательность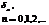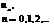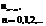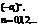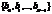
z-образ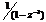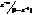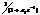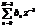

Обратное Z–преобразование решает задачу восстановления оригинала по известному изображению, используя следующее соотношение 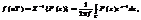(1.3) где С – контур сходимости 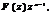охватывающий начало координат z-плоскости.

Такой интеграл решить сложно, поэтому существуют более простые способы нахождения обратного z-преобразования: с использованием таблицы соответствия, на основании теоремы Коши о вычетах или разложением изображения на простые дроби.

Основные свойства z-преобразования сводятся к следующему:

1 Линейность. Есл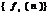и и 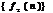- решетчатые функции, а 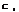и 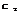- постоянные действительные коэффициенты, то 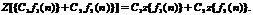(1.4)

2 Сдвиг последовательности (задержка). Если последовательность 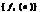имеет z-преобразование 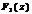, то задержанная на m интервалов последовательность 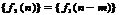, имеет z-преобразование 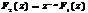(1.5)

Таким образом, задержка сигнала на m интервалов дискретизации во временной области эквивалентна умножению на 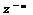в z-области.

3 Свертка последовательностей. Если последовательност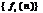и и 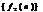имеют z-преобразования 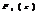и 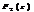, то последовательность 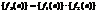, представляющая собой свертку исходных последовательностей 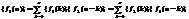, имеет z-преобразование 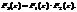Вывод: свертка сигналов во временной области эквивалентна умножению z-образов в z-области.

Для описания дискретных сигналов в частотной области используется спектр, который связан с дискретным сигналом парой преобразований Фурье. Спектром 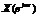или фурье-изображением дискретного сигнала называют прямое преобразование Фурье дискретной последовательности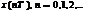 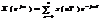, (1.6) где 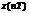- оригинал (дискретная последовательность).

Из формулы (1.6) следует, что спектр является периодической функцией по частоте с периодом, равным частоте дискретизации 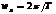. Модуль и аргумент спектра также являются периодическими функциями с тем же периодом, причем модуль спектра - четная, а аргумент – нечетная функции.

Обратное преобразование Фурье для дискретной последовательности 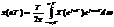(1.7)

Если сравнить формулы (1.6) и (1.1), то можно увидеть, что преобразование Фурье представляет собой частный случай z–преобразования: 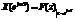.Свойства спектра дискретного сигнала следуют из свойств z-преобразования.