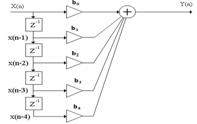
Передаточная функция и прямая структура нерекурсивного фильтра 4-го порядка

Суммарный шум квантования на выходе цифровой цепи

В цифровых системах обработки сигналов отсчеты обрабатываемого сигнала y(n), x(n), коэффициенты разностного уравнения или передаточных функций, а также результаты выполнения арифметических операций в сумматорах и умножителях представляются b-разрядными двоичными числами в соответствии с разрядностью регистров, ячеек памяти и операционных устройств. Такое приближенное представление чисел называют квантованием. Квантование – нелинейная операция, поэтому при ее введении в алгоритм обработки сигнала, который описывается линейным дискретным уравнением, возникают ошибки в реализации алгоритма. Такие ошибки называются ошибками квантования.

Линейные модели процессов аналого-цифрового преобразования и умножения (с конечным числом разрядов) и аддитивным шумом e(n) идентичны, их свойства описываются одинаковыми выражениями для математического ожидания и дисперсии ошибок квантования, поэтому 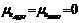; 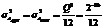, (6.5)

где e_АЦП(n) и e_УМН(n) - шумы АЦП и умножителя соответственно.

Для оценки влияния квантования входного сигнала (шум АЦП) на выходной шум цифровой цепи полагаем, что коэффициенты и арифметические операции реализуются точно. Выходной шум, как реакция дискретной цепи, имеющей импульсную характеристику h(n), на входной шум e_АЦП(n) определяется по формуле 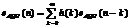. (6.6)

Максимальные ошибки квантования входного (при округлении) и выходного сигнала определяются по формулам 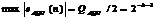, (6.7)

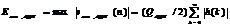. (6.8)

Дисперсия составляющей выходного шума, обусловленной АЦП

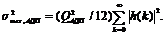(6.9)

Шум на выходе цифровой цепи имеет еще одну составляющую, обусловленную квантованием результатов умножения (собственный шум).

Максимальная ошибка и дисперсия шума квантования на выходе цифровой цепи первого порядка определяются с учетом этой составляющей

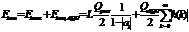; (6.10)

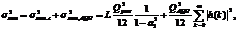(6.11)

где Е_{вых. с} - максимальное значение ошибки составляющей выходного собственного шума;

σ²_{вых. с}- дисперсия составляющей выходного собственного шума;

h(k)- импульсная характеристика цепи первого порядка;

L - количество умножителей.

Максимальная ошибка квантования на выходе цифровой цепи второго порядка определяется как 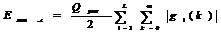, (6.12)

где g_i(k) - импульсная характеристика от выхода i – го умножителя до выхода цепи.

Дисперсия выходного шума звена второго порядка для всех i = 1,2,…,L определяется следующей формулой

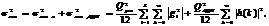(6.13)

где h(k) - импульсная характеристика цепи второго порядка.

Каноническая структура 1 рекурсивного фильтра второго порядка

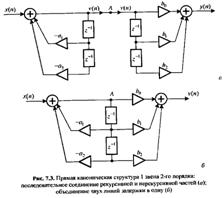
На рис. 7.3, а показана прямая структура звена 2-го порядка в виде последовательного соединения рекурсивной (7.2) и нерекурсивной (7.3) частей.

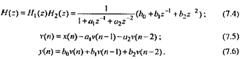
Объединение двух линий задержки в одну (на основании равенства входного и выходного сигналов в точке А) приводит к прямой канонической структуре 1 (рис. 7.3.б).

Формат команд сигнального процессора TMS 32010 с прямой адресацией. Примеры команд.

Для формирования адреса ячейки памяти при прямой адресации семь младших разрядов слова команды объединяются с содержимым указателя страницы (DP) памяти данных, т.е. реализуется следующая схема разделения памяти на страницы:

DP Номер ячеек памяти

0 0…127

1 128…144

Формат команд с прямой адресацией:

15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Код операции 0 Прямой адрес памяти

Седьмой разряд Р7 = 0 определяет режим прямой адресации.

Формат команд сигнального процессора TMS 32010 с косвенной адресацией. Примеры команд.

В режиме косвенной адресации в качестве адреса памяти данных используются 8 младших разрядов одного из вспомогательных регистров (AR0 и AR1), при этом нет необходимости разделения памяти данных на страницы. Текущий вспомогательный регистр выбирается с помощью указателя вспомогательного регистра ARP. При выполнении любой команды с косвенной адресацией вспомогательные регистры можно установить в режиме автоинкремента/автодекремента (увеличить/уменьшить значение вспомогательного регистра на 1), а также изменить содержимое указателя вспомогательного регистра ARP. Содержание вспомогательного регистра и ARP изменяются после окончания выполнения текущей команды.

Формат команд с косвенной адресацией:

15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Код операции 1 0 INC DEC ARP 0 0 ARP

Седьмой разряд Р7 = 1 определяет режим прямой адресации. В разрядах 6-0 содержатся биты управления косвенной адресацией.

Если третий разряд нулевой Р3=0, то содержимое нулевого разряда Р0 загружается в ARP.

Если в третьем разряде содержится единица Р3=1, то содержимое ARP остается прежним.

Если в пятом разряде содержится единица Р5=1, то содержимое текущего вспомогательного регистра увеличивается на 1 после выполнения текущей команды.

Если Р4=1, то содержимое текущего вспомогательного регистра уменьшается на 1.

Если в 4-м и 5-м разрядах нули, то операции инкремента/декремента не выполняются.

Разряды 6, 2, 1 являются резервными и должны всегда содержать нули.

Прямая и косвенная адресация могут быть использованы со всеми командами, использующими операнды данных, за исключением команд, обрабатывающих непосредственные операнды (LDPK, LARK, MPYK, LACK), которые извлекают операнд непосредственно из кода команды.

Формат команд сигнального процессора TMS 32010 с косвенной адресацией. Примеры команд.

LAC-Загрузка аккумулятора со сдвигом: 1 цикл, 1 слово, код регистра команды «0 0 1 0 <--S--> I <---- D ---->» (S – сдвиг, D – адрес памяти данных).

SACH-Запись старших разрядов аккумулятора со сдвигом: 1 цикл, 1 слово, код регистра команды «0 1 0 1 1 <-S-> I <---- D ---->»

Пример программы использующей команды с косвенной адресацией:

LARP 0; Загрузка 0 в АRР. Т.е. после этой команды активным индексным регистром становится АR0.

LARK 0,13; Загрузка константы 13 в индексный регистр АRO.

LARK 1,140; Загрузка константы 140 в индексный регистр АR1.

LAC *+,0,1; Перепись содержимого 13 ячейки памяти (адресуется содержимым активного индексного регистра AR0) в младшие разряды аккумулятора с нулевым сдвигом, инкрементация 0-го индексного регистра (АR0 <--- 14), модификация АRР (АRР <--- 1), т.е. после этой команды активным становится АR1.

SACL *+,0; Перепись содержимого младших разрядов аккумулятора (адресуется содержимым активного индексного регистра AR1) в 12-ю ячейку 1 страницы памяти (140), инкрементация 1- го индексного регистра (АR1 <--- 141), модификация АRР (АRР <--- 0).

LAC *,0,1; Перепись 14 ячейки в младшие разряды аккумулятора.

SACL *; Перепись содержимого младших разрядов аккумулятора в 13-ю ячейку первой страницы памяти (141).

Таким образом, вся эта небольшая программа осуществляет перенос массива данных из 13, 14 в 140, 141 ячейки памяти. Очевидный выигрыш в данном случае заключается в том, что не нужно переустанавливать активную страницу памяти, поскольку косвенно можно адресовать любую ячейку ОЗУ данных. Выигрыш по сравнению с использованием прямой адресации тем больше, чем больше объем переносимых массивов.

Необходимо отметить, что инкрементация/декрементация индексного регистра и модификация указателя активного индексного регистра осуществляется после выполнения самой команды.

Модели квантования.

Рис.1 Гарворд-ая архитектура

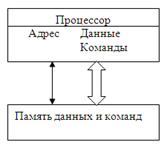
Рис.2 Архитектура Фон Неймана

Каска

Передаточная функция и прямая структура нерекурсивного фильтра 4-го порядка

В z-области основной характеристикой ЛДС является z-изображение импульсной характеристики h(n), которое определяется с помощью Z-преобразования: 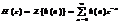и называется передаточной функцией (ПФ). Это математическое определе­ние ПФ. По известному z-изображению импульсная характеристика Н(п) находится с помощью обратного Z-преобразования: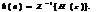

В z-области, согласно теореме о свертке, при нулевых началь­ных условиях соответствует уравнение Y(z) = H(z)X(z), где X(z) и Y(z) —z-изображения воздействия и реакции соответственно. Это позволяет представить передаточную функцию как отношение: 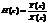и определить ее подобно передаточной функции линейных аналоговых систем.

Передаточной функцией H(z) линейной дискретной системы называется отношение z-изображения реакции к z-изображению воздействия при нуле­вых начальных условиях.

Импульсная характеристика h(n) представляет собой реакцию на воздействие в виде цифро­вого единичного импульса u₀(n), то, подставив z-изображения данных сигналов в Н(z) учитывая, что Z{u₀(n)}=1, получим H(z):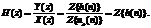

ПФ общего вида: 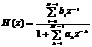представляет собой дробно-рациональную функцию, числитель и знаменатель которой являются многочленами относительно z^-1 порядков (N-1) и (М-1) с вещественными коэффициентами b_i и a_k соот­ветственно.

Порядок передаточной функции равен max {(M-1), (N-1)}.

Как любая дробно-рациональная функция, ПФ характеризуется особыми точками (полюсами) и пулями. Нулями называют значения z, при которых ПФ равна нулю.

Особыми точками (полюсами) называют значения z, при которых знамена­тель ПФ равен нулю. Особые точки и нули ПФ линейных дискретных систем находятся аналогич­но тому, как это делается для ПФ линейных аналоговых цепей. Предвари­тельно необходимо записать H(z) как дробно-рациональную функцию

относительно положительных степеней z, для чего числитель и знаменатель Н(z) следует умножить на z^M-1: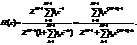

1 Передаточная функция H(z) представляет собой неправильную дробно-рациональную функцию: порядок многочлена числителя равен порядку многочлена знаменателя (N-1) = (М-1). Тогда в результате умножения числителя и знаменателя Н(z) на Z^M-1 имеем: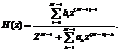

Нулями данной передаточной функции являются корни уравнения числи­теля (корни числителя): 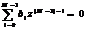, а полюсами — корни уравнения знаменателя (корни знаменателя): .

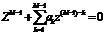Если среди полюсов или нулей встречаются одинаковые, их называют кратными.

2 Передаточная функция H(z) представляет собой правильную дробно-рациональную функцию: порядок многочлена числителя (L-1) меньше порядка многочлена знаменателя (М -1): (L-1)<(M-1), где (L-1) может принимать значения (L-1)=0,1,…, (M-2).

Полюсы передаточной функции H(z) определяются так же, как в первом случае. Что касается нулей, то помимо (L-1) корней числителя добавля­ются нули z=∞, кратность которых равна разности порядков многочле­нов знаменателя и числителя: (M-1)-(L-1) = M-L. Эти нули не считаются информативными, поэтому часто их опускают.

Например, имеем ПФ второго порядка: 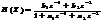. После умножения числителя и знаменателя на z^M-1=z² получим ПФ: 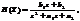представляющую собой правильную дробь, у которой порядок числителя (L-l) = l на единицу меньше порядка знаменателя (М -1) = 2: (M-1)-(L-1)=M-L=1. Следовательно, такая ПФ имеет два нуля: один - корень числителя: 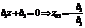и второй — неинформативный: .

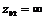Нули и полюсы передаточной функции удобно изображать в виде точек на комплексной z-плоскости. Положение точек определяется их координатами, чаше всего полярными. Нули изображаются кружками (о), а полюсы — звез­дочками ( * ). Совокупность нулей (о) и полюсов (*) на z-плоскости называ­ют картой нулей и полюсов. Такая карта — одна из важнейших графических характеристик ЛДС.