Просеивание потоков. Потоки Эрланга

Допустим, что ко всем вызовам потока заявок применяется следующий алгоритм фильтрации: с вероятностью 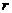заявка поступает в СМО, а с вероятностью 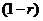теряется. Поток вызовов, поступающих в СМО, называется просеянным. Процедура фильтрации называется рекуррентной операцией просеивания. Поток вызовов, поступающих в СМО, будет рекуррентным.

Из простейшего потока с параметром 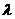рекуррентная операция просеивания создает также простейший поток с параметром 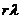. Это означает, что разделение простейшего потока на ряд компонентов, которое осуществляется с помощью рекуррентной операции просеивания, формирует несколько простейших потоков. Параметр каждого потока определяется произведением 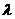на величину соответствующей вероятности.

Если процедура просеивания отлична от рекуррентной, то характер потока заявок будет меняться. Например, 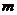заявок теряются, а 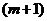поступает в СМО и так далее. В этом случае из простейшего потока формируется поток Эрланга 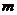-го порядка. В потоках Эрланга любого порядка интервалы времени между вызовами независимы и распределены по одному и тому же закону. Поэтому потоки Эрланга относятся к классу рекуррентных. Для математического ожидания и дисперсии интервала времени между вызовами в потоке Эрланга 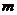-го порядка справедливы такие формулы:

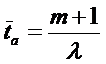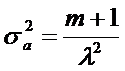, . (13)

Это означает, что коэффициент вариации исследуемой величины ( 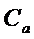) определяется по такой формуле:

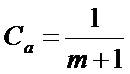. (14)

Если вызовы не теряются, то коэффициент вариации равен единице, то есть поток является простейшим. При 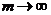поток становится похожим на детерминированный. Параметр просеянного потока определяется очевидным соотношением:

.

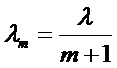Длительность обслуживания

Длительность обслуживания поступившего вызова может быть детерминированной или случайной. Детерминированная длительность задается последовательностью величин 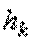, характеризующих длительность обслуживания 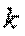-го вызова и при 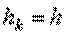длительность обслуживания является постоянной величиной. Детерминированная длительность обслуживания имеет место в случае цифровых систем с пакетной коммутацией, где заголовок пакета составляет постоянную величину и для его передачи требуется одно и то же время. В большинстве случаев общая длительность обслуживания вызова 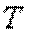является случайной величиной.

Случайная длительность задается функцией распределения или ПРВ. Наиболее распространенной функцией распределения случайной длительности обслуживания является показательная функция

,

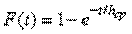где 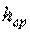- средняя длительность обслуживания одного вызова.

ПРВ величины 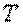можно найти путем дифференцирования функции распределения:

,

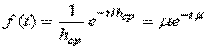где 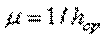- интенсивность потока обслуживания.

Математическое ожидание величины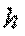

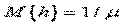
а дисперсия и среднеквадратическое отклонение

; .

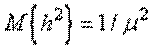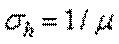Для упрощения математических выражений часто за единицу измерения длительности обслуживания принимают математическое ожидание СВ :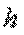

,

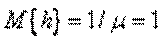откуда следует, что величина .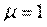

Нагрузка и ее виды

Нагрузка и ее интенсивность измеряются в Эрлангах (Эрл). Интенсивность поступающей нагрузки в 1Эрл создается потоком поступающих вызовов с интенсивностью в один вызов за среднее время занятия канала связи.

Обслуженная нагрузка – это общее время занятия каналов связи за период времени, равный средней длительности обслуживания :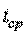

,

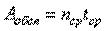где 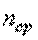- среднее число занятых каналов связи в течение времени .

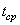Интенсивностью обслуженной нагрузки называется среднее число занятых каналов связи за время :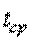

.

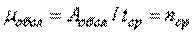Потерянная нагрузка представляет собой разность между поступающей и обслуженной нагрузками:

.

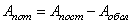Таким образом, поступившая заявка может быть либо обслужена, либо отброшена. В соответствии с этим различают три типа систем распределения информации: без потерь, с потерями и с ожиданием.

Системы без потерь возможны только в том случае, когда число источников вызовов 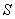меньше или равно числу каналов связи 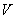. Очевидно, что выполнить это условие не всегда возможно и экономически оправданно, поэтому часто в системах связи имеет место соотношение 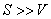, в результате возникают потери 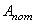. Третий тип систем позволяет избежать потерь за счет использования очереди заявок, заставших все каналы занятыми. В таких системах объем поступающей и обслуженной нагрузок одинаковый, т.к. поступивший вызов либо обслуживается сразу, либо встает очередь до освобождения канала связи. Таким образом, вызов не теряется, а лишь задерживается на некоторое время.

Характеристикой качества всех трех видов систем распределения информации является вероятность обслуживания заявки :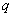

,

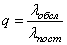или вероятность отказа в обслуживании :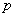

.

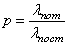Величина 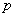получила название вероятность блокировки вызова. При этом за единицу измерения качества обслуживания принята тысячная доля единицы или промилле: .

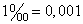Кроме потерь по вызовам существуют еще потери по нагрузке 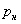и по времени 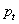. Вероятность потерь по нагрузке определяется выражением

,

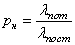а по времени

,

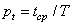где 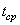- среднее время занятости каналов связи; 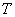- общее время работы системы распределения информации.

Для оценивания качества систем с ожиданием используется вероятность превышения времени ожидания 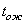заданной величине :

.

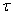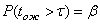Если величина 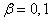, то система распределения информации имеет высокое качество обслуживания, при 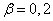- пониженное. Вероятность 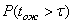рассчитывается на основе накопленной статистики: числа вызовов простоявших в очереди времени больше величины 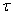и общего числа поступивших заявок:

.

12.Основные параметры и расчет интенсивности нагрузкиОсновными параметрами нагрузки являются: число источников нагрузки . n;

среднее число вызовов, поступающих от одного источника нагрузки в единицу времени, . с(штрих);

средняя длительность занятия коммутационной системы пря обслуживании одного вызова . t(штрих).

Принципы проектирования основных параметров нагрузки рассмотрим на примере их проектирования для местных телефонных сетей.

Число источников нагрузкиn. По среднему числу вызовов и средней длительности занятия на ГТС различают следующие категории источников телефонной нагрузки: телефонные аппараты народнохозяйственного сектора . n_нх; квартирные телефонные аппараты, которые делятся на квартирные аппараты индивидуального пользования . n_к.и и квартирные аппараты коллективного пользования . п_к._к; таксофоны . n_т; соединительные линии от учрежденческих телефонных станций . n_сл. Таким образом

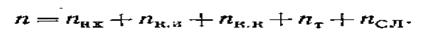
Среднее число вызовов от одного источника в единицу временис. В соответствии с имеющимися категориями источников нагрузки среднее число вызовов в единицу времени от

одного телефонного аппарата народнохозяйственного сектора обозначается через с_нх, от квартирного аппарата индивидуального пользования . c_к.и, коллективного пользования . c_к.к, от таксофона . c_т, от соединительной линии . c_сл. Обозначим в общем виде через c_i среднее число вызовов от источников i-й категории, п_i. число источников i-й категории. Тогда при k категориях источников нагрузки на АТС средневзвешенное число вызовов от одного источника определится из выражения

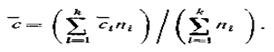
Средняя длительность занятияt. Под длительностью одного занятия понимается промежуток времени с момента снятия абонентом микротелефона (замыкание шлейфа абонентской линии) до момента возвращения приборов станции, занятых в обслуживании вызова, в исходное состояние.

Длительность занятия зависит в основном от действий абонентов и частично от систем АТС. Следовательно, длительность занятия является случайной величиной и ее среднее значение может быть определено только на основании результатов наблюдений на действующих сетях.

Разговор состоялся. Средняя длительность этого вида занятия может быть рассчитана по формуле

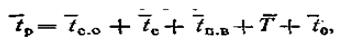
где (штрих)t_с.о, t_с, t_п.в, Т, t_o. средние продолжительности соответственно слушания абонентом сигнала ответа станции, установления соединения, посылки вызова вызываемому

абоненту, разговора, возвращения приборов в исходное состояние после отбоя.

Средняя интенсивность поступающей нагрузки.Проектирование средней интенсивности поступающей нагрузки основывается на результатах наблюдений за параметрами нагрузки на действующих АТС и предположении о тенденции изменения этих параметров с развитием ГТС.

Величина интенсивности нагрузки может быть рассчитана поформуле