Симметричный и примитивный потоки

Симметричным потоком называется поток с простым последействием, параметр которого λ_s(t) в любой момент времени t зависит только от числа i обслуживаемых в этот момент вызовов и не зависит от других характеристик, определяющих состояние s(t) коммутационной системы. При этом зависимость параметра от числа обслуживаемых вызовов может быть подчинена любому закону. Поэтому в любом состоянии s(t) с i обслуживаемыми вызовами параметр симметричного потока один и тот же, он зависит только от i, т. е. λ_s(t)=λ_i.

Примитивным называется такой симметричный поток, параметр которого λ_i прямо пропорционален числу свободных в данный момент источников:

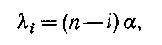где n . общее число источников вызовов; i . число занятых источников; α . параметр потока источника в свободном состоянии (при этом имеет место естественное предположение . занятый источник не может производить вызовы).

Поток с простым последействием является более общим по сравнению с простейшим потоком вызовов. Простейший поток можно представить частным случаем потока с простым последействием, в том числе симметричного и примитивного потоков. С увеличением числа источников п и уменьшением параметра α последействие потока уменьшается. В предельном случае при п→∞ и α→0 так, что пα есть конечная величина и i принимает ограниченные значения, параметр потока λ=nα не зависит от состояния системы, т. е. модель примитивного потока переходит в модель простейшего потока вызовов.

Поток с повторными вызовами

Система, на которую поступает поток вызовов, обслуживает не все поступающие вызовы. Часть из них не обслуживается (теряется) по ряду причин. Так, например, на телефонных сетях часть вызовов не обслуживается по причине занятости или неответа вызываемого абонента, ошибок вызывающего абонента в процессе набора номера, занятости всех соединительных устройств, способных обслужить поступивший вызов, неустановления соединения коммутационной системой по техническим причинам. Все или часть источников необслуженных вызовов осуществляют повторные вызовы.

Поток с повторными вызовами состоит из первичных и повторных вызовов. Поскольку параметр потока повторных вызовов зависит от состояния коммутационной системы, то и поток с повторными вызовами относится к классу потоков с простым последействием.

Параметр потока повторных вызовов можно определить как произведение числа источников повторных вызовов j на параметр одного источника β. В качестве модели потока первичных вызовов принимается простейший с параметром λ или примитивный с параметром λ_iпоток. Параметр суммарного потока равен сумме параметров потоков первичных и повторных вызовов. Для простейшего и примитивного потоков он соответственно составляет.

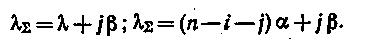
Поток освобождений.

Потоком освобождений именуется последовательность моментов окончания обслуживания вызовов. В общем случае характеристики потока освобождений зависят от параметров поступающего потока вызовов, свойства работы коммутационной системы и закона распределения времени обслуживания.

При неизменной продолжительности обслуживания h всех вызовов без утрат характеристики потока освобождений совпадают со качествами поступающего потока вызовов.

Происходит лишь сдвиг по времени на величину h меж моментом поступления вызова и моментом окончания его обслуживания.

При показательном законе распределения продолжительности обслуживания моменты окончания обслуживания не зависят от моментов поступления вызовов. Потому характеристики потока освобождений в данном случае не зависят от параметров поступающего потока вызовов и свойства работы коммутационной системы и стопроцентно определяются числом обслуживаемых вызовов.

Пусть в коммутационной системе в момент t занято к линий (к источников находятся на обслуживании), тогда возможность освобождения i линий за просвет времени z можно разглядывать как i удачных испытаний при общем числе к независящих испытаний. Тогда согласно распределению.

Таковым образом, параметр потока освобождений пропорционален числу занятых линий, т. е. числу вызовов, которые находятся на обслуживании. Коэффициентом пропорциональности служит параметр продолжительности обслуживания вызовов (ft = jh), который можно интерпретировать как интенсивность источника в занятом состоянии. Как следует, поток освобождений по своим свойствам подобен простому сгустку.