Принципы классификации потоков вызовов

Потоки вызовов классифицируются с точки зрения стационарности, ординарности и последействия.

Стационарность потока.Поток вызовов является стационарным, если при любом п совместный закон распределения числа вызовов за промежутки времени [t₀, t₁), [t₀, t₂), ..., [t₀, t_n)

зависит только от длины промежутков времени и не зависит от момента t₀. Иными словами, независимо от того, где на оси времени расположен промежуток времени [t₀, t₁), вероятность поступления K(t₀, t_t) вызовов одна и та же.

Ординарность потока

Ординарность потока выражает практическую невозможность одновременного поступления двух и более вызовов в любой момент времени t. Примером ординарного потока является поток вызовов, поступающий на телефонную станцию от абонентской группы любой емкости. Потоки телефонных вызовов к абонентам диспетчерской или конференц-связи, потоки телеграмм в несколько адресов являются неординарными.

Последействие потока

Поток вызовов является потоком с последействием, если вероятность поступления того или иного числа вызовов за некоторый промежуток времени зависит от процесса поступления вызовов до начала этого промежутка. Потоки вызовов от спаренных телефонных аппаратов, от малых абонентских групп, в направлениях коммутационной системы, не обеспечивающих удовлетворительного качества обслуживания абонентов телефонной связью, к интенсивно загруженным абонентам являются потоками с последействием.

Характеристики потоков вызовов

К основным характеристикам потока вызовов следует отнести ведущую функцию потока, его параметр и интенсивность.

Под параметром потока λ(t) в момент времени t понимается предел отношения вероятности поступления хотя бы одного вызова за время [t, t + τ) к длине этого отрезка времени τ при τ→0: . е. параметр потока есть плотность вероятности наступления вызывающего момента в момент t. Исходя из (2.8), находим вероятность поступления одного и более вызовов за время [t, t + τ):

Интенсивностью стационарного потока μ называется математическое ожидание числа вызовов, поступающих в единицу времени. Единица времени может быть выбрана произвольно, однако в теории телетрафика в качестве такой единицы большей частью принимают среднюю длительность одного занятия. Вследствие аддитивности математического ожидания для стационарного потока ведущая функция за промежуток времени [0, t) равна Λ(0, t)=μt.

Простейший поток вызовов

Определение.Простейшим потоком называется стационарный ординарный поток без последействия. Простейший поток вызовов является наиболее распространенной моделью реального потока вызовов, применяемой в системах массового обслуживания, в том числе в теории телетрафика.

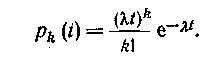
Таким образом, вероятность поступления точно k вызовов простейшего потока за отрезок времени t определяется формулой Пуассона. По этой причине простейший поток также называют стационарным пуассоновским потоком.

оток однородных событий называется простейшим, если он обладает следующими тремя свойствами.

Стационарность. Для любого положительного t (t>0) всегда существует такое k>=0, что вероятность появления k событий за период времени (a, a+t), обозначим ее через p_k(t), является одной и той же для всех a>=0. Для потоков, в которых за конечный промежуток времени с вероятностью 1 происходит конечное число событий, всегда выполняется равенство 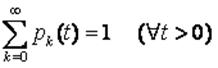. Таким образом, сущность данного свойства заключается в постоянстве вероятностного режима во времени, или другими словами, вероятностные характеристики потока не зависят от времени.

Отсутствие последействия. Оно выражает собой отсутствие взаимной зависимости появления событий в потоке в непересекающихся между собой промежутках времени. В данном случае условная вероятность появления k событий (в зависимости от возможных вариантов чередования до начального момента времениa) за промежуток времени (a, a+t) равняется безусловной вероятности p_k(t). Таким образом, появление в потоке очередного события не зависит от чередования предшествующих моменту a событий и как давно произошло последнее из них.

Ординарность. Это означает, что вероятность появления в стационарном потоке за промежуток времени 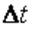более чем одного события является бесконечно малой величиной o(t) более высокого порядка чем .

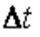В итоге получаем следующее окончательное определение простейшего потока.