Теория телетрафика . одна из ветвей теории массового обслуживания

Теория телетрафика . одна из ветвей теории массового обслуживания

Количественная сторона процессов массового обслуживания является предметом раздела прикладной математики, которую советский математик А. Я. Хинчин (1894.1959 гг.) назвал теорией массового обслуживания. Родилась теория массового обслуживания в первой четверти XX века вследствие возникновения потребностей разработки математических методов для оценки качества функционирования телефонных систем. Основоположником теории телетрафика, из которой «выросла» теория массового обслуживания, является датский ученый А. К. Эрланг (1878.1929 гг.).сотрудник Копенгагенской телефонной компании.

В теории массового обслуживания все рассматриваемые объекты объединяются под общим названием «системы массового обслуживания». Одним из классов систем массового обслуживания являются системы распределения информации (системы телетрафика). Системой распределения информации могут быть совокупность коммутационных приборов, часть или весь коммутационный узел либо сеть связи, которые обслуживают по определенному алгоритму телефонные, телеграфные и другие сообщения.

В настоящее время методы теории массового обслуживания используются для решения самого широкого круга задач . от бытового обслуживания до космических исследований, однако определяющую роль в развитии теории массового обслуживания продолжает играть одна из ее ветвей . теория телетрафика.

Предметом теории телетрафика является количественная, сторона процессов обслуживания потоков сообщений в системах распределения информации.

Математические модели систем распределения информации

Математическую модель обозначают последовательностью символов. Первый символ обозначает функцию распределения промежутков между вызовами, второй . функцию распределения длительности обслуживания, третий и последующие символы . схему и дисциплину обслуживания. Для обозначения распределений введены следующие символы: М . показательное, Е . эрланговское, D . равномерной плотности, G . произвольное. Для многомерного случая над символами ставятся стрелки. Схема системы телетрафика обозначается символом S. Если схема представляет собой полнодоступный пучок линий, то вместо S пишется υ, где υ . число линий. Если вызовы обслуживаются с ожиданием, то число мест для ожидания обозначают символом r. Символ f с индексами вводится для обозначений приоритетов в обслуживании.

Приведем несколько примеров. Так, M/M/S обозначает схему S, на которую поступает поток с показательной функцией распределения промежутков между вызовами и показательной функцией распределения длительности обслуживания (простейший поток 00////frGMkk∞<υвызовов). Запись М/М/υ<∞ обозначает полнодоступный пучок с конечным числом линий, который обслуживает с потерями простейший поток вызовов. Запись rr обозначает полнодоступный пучок из υ линий, который обслуживает с ожиданием k потоков с показательными функциями распределения промежутков между вызовами; каждый поток имеет произвольную функцию распределения длительности обслуживания; число мест для ожидания r < ∞; постановка вызовов в очередь осуществляется без приоритетов . f ⁰, выборка из очереди . также без приоритетов . f₀.

Построение математической модели, адекватно отображающей реальную систему распределения информации, во многих случаях является нетривиальной задачей. От правильного выбора модели в конечном счете зависит успех решения всей задачи.

Принципы классификации потоков вызовов

Потоки вызовов классифицируются с точки зрения стационарности, ординарности и последействия.

Стационарность потока.Поток вызовов является стационарным, если при любом п совместный закон распределения числа вызовов за промежутки времени [t₀, t₁), [t₀, t₂), ..., [t₀, t_n)

зависит только от длины промежутков времени и не зависит от момента t₀. Иными словами, независимо от того, где на оси времени расположен промежуток времени [t₀, t₁), вероятность поступления K(t₀, t_t) вызовов одна и та же.

Ординарность потока

Ординарность потока выражает практическую невозможность одновременного поступления двух и более вызовов в любой момент времени t. Примером ординарного потока является поток вызовов, поступающий на телефонную станцию от абонентской группы любой емкости. Потоки телефонных вызовов к абонентам диспетчерской или конференц-связи, потоки телеграмм в несколько адресов являются неординарными.

Последействие потока

Поток вызовов является потоком с последействием, если вероятность поступления того или иного числа вызовов за некоторый промежуток времени зависит от процесса поступления вызовов до начала этого промежутка. Потоки вызовов от спаренных телефонных аппаратов, от малых абонентских групп, в направлениях коммутационной системы, не обеспечивающих удовлетворительного качества обслуживания абонентов телефонной связью, к интенсивно загруженным абонентам являются потоками с последействием.

Простейший поток вызовов

Определение.Простейшим потоком называется стационарный ординарный поток без последействия. Простейший поток вызовов является наиболее распространенной моделью реального потока вызовов, применяемой в системах массового обслуживания, в том числе в теории телетрафика.

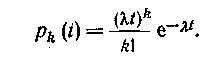
Таким образом, вероятность поступления точно k вызовов простейшего потока за отрезок времени t определяется формулой Пуассона. По этой причине простейший поток также называют стационарным пуассоновским потоком.

оток однородных событий называется простейшим, если он обладает следующими тремя свойствами.

Стационарность. Для любого положительного t (t>0) всегда существует такое k>=0, что вероятность появления k событий за период времени (a, a+t), обозначим ее через p_k(t), является одной и той же для всех a>=0. Для потоков, в которых за конечный промежуток времени с вероятностью 1 происходит конечное число событий, всегда выполняется равенство 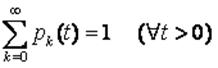. Таким образом, сущность данного свойства заключается в постоянстве вероятностного режима во времени, или другими словами, вероятностные характеристики потока не зависят от времени.

Отсутствие последействия. Оно выражает собой отсутствие взаимной зависимости появления событий в потоке в непересекающихся между собой промежутках времени. В данном случае условная вероятность появления k событий (в зависимости от возможных вариантов чередования до начального момента времениa) за промежуток времени (a, a+t) равняется безусловной вероятности p_k(t). Таким образом, появление в потоке очередного события не зависит от чередования предшествующих моменту a событий и как давно произошло последнее из них.

Ординарность. Это означает, что вероятность появления в стационарном потоке за промежуток времени 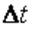более чем одного события является бесконечно малой величиной o(t) более высокого порядка чем .

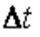В итоге получаем следующее окончательное определение простейшего потока.

Поток с повторными вызовами

Система, на которую поступает поток вызовов, обслуживает не все поступающие вызовы. Часть из них не обслуживается (теряется) по ряду причин. Так, например, на телефонных сетях часть вызовов не обслуживается по причине занятости или неответа вызываемого абонента, ошибок вызывающего абонента в процессе набора номера, занятости всех соединительных устройств, способных обслужить поступивший вызов, неустановления соединения коммутационной системой по техническим причинам. Все или часть источников необслуженных вызовов осуществляют повторные вызовы.

Поток с повторными вызовами состоит из первичных и повторных вызовов. Поскольку параметр потока повторных вызовов зависит от состояния коммутационной системы, то и поток с повторными вызовами относится к классу потоков с простым последействием.

Параметр потока повторных вызовов можно определить как произведение числа источников повторных вызовов j на параметр одного источника β. В качестве модели потока первичных вызовов принимается простейший с параметром λ или примитивный с параметром λ_iпоток. Параметр суммарного потока равен сумме параметров потоков первичных и повторных вызовов. Для простейшего и примитивного потоков он соответственно составляет.

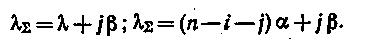
Поток освобождений.

Потоком освобождений именуется последовательность моментов окончания обслуживания вызовов. В общем случае характеристики потока освобождений зависят от параметров поступающего потока вызовов, свойства работы коммутационной системы и закона распределения времени обслуживания.

При неизменной продолжительности обслуживания h всех вызовов без утрат характеристики потока освобождений совпадают со качествами поступающего потока вызовов.

Происходит лишь сдвиг по времени на величину h меж моментом поступления вызова и моментом окончания его обслуживания.

При показательном законе распределения продолжительности обслуживания моменты окончания обслуживания не зависят от моментов поступления вызовов. Потому характеристики потока освобождений в данном случае не зависят от параметров поступающего потока вызовов и свойства работы коммутационной системы и стопроцентно определяются числом обслуживаемых вызовов.

Пусть в коммутационной системе в момент t занято к линий (к источников находятся на обслуживании), тогда возможность освобождения i линий за просвет времени z можно разглядывать как i удачных испытаний при общем числе к независящих испытаний. Тогда согласно распределению.

Таковым образом, параметр потока освобождений пропорционален числу занятых линий, т. е. числу вызовов, которые находятся на обслуживании. Коэффициентом пропорциональности служит параметр продолжительности обслуживания вызовов (ft = jh), который можно интерпретировать как интенсивность источника в занятом состоянии. Как следует, поток освобождений по своим свойствам подобен простому сгустку.

Длительность обслуживания

Длительность обслуживания поступившего вызова может быть детерминированной или случайной. Детерминированная длительность задается последовательностью величин 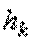, характеризующих длительность обслуживания 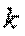-го вызова и при 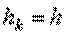длительность обслуживания является постоянной величиной. Детерминированная длительность обслуживания имеет место в случае цифровых систем с пакетной коммутацией, где заголовок пакета составляет постоянную величину и для его передачи требуется одно и то же время. В большинстве случаев общая длительность обслуживания вызова 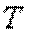является случайной величиной.

Случайная длительность задается функцией распределения или ПРВ. Наиболее распространенной функцией распределения случайной длительности обслуживания является показательная функция

,

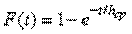где 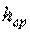- средняя длительность обслуживания одного вызова.

ПРВ величины 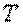можно найти путем дифференцирования функции распределения:

,

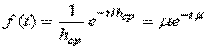где 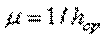- интенсивность потока обслуживания.

Математическое ожидание величины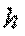

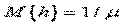
а дисперсия и среднеквадратическое отклонение

; .

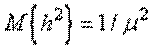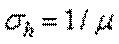Для упрощения математических выражений часто за единицу измерения длительности обслуживания принимают математическое ожидание СВ :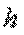

,

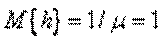откуда следует, что величина .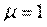

Нагрузка и ее виды

Нагрузка и ее интенсивность измеряются в Эрлангах (Эрл). Интенсивность поступающей нагрузки в 1Эрл создается потоком поступающих вызовов с интенсивностью в один вызов за среднее время занятия канала связи.

Обслуженная нагрузка – это общее время занятия каналов связи за период времени, равный средней длительности обслуживания :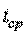

,

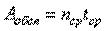где 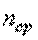- среднее число занятых каналов связи в течение времени .

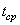Интенсивностью обслуженной нагрузки называется среднее число занятых каналов связи за время :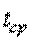

.

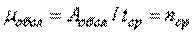Потерянная нагрузка представляет собой разность между поступающей и обслуженной нагрузками:

.

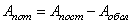Таким образом, поступившая заявка может быть либо обслужена, либо отброшена. В соответствии с этим различают три типа систем распределения информации: без потерь, с потерями и с ожиданием.

Системы без потерь возможны только в том случае, когда число источников вызовов 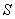меньше или равно числу каналов связи 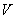. Очевидно, что выполнить это условие не всегда возможно и экономически оправданно, поэтому часто в системах связи имеет место соотношение 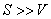, в результате возникают потери 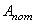. Третий тип систем позволяет избежать потерь за счет использования очереди заявок, заставших все каналы занятыми. В таких системах объем поступающей и обслуженной нагрузок одинаковый, т.к. поступивший вызов либо обслуживается сразу, либо встает очередь до освобождения канала связи. Таким образом, вызов не теряется, а лишь задерживается на некоторое время.

Характеристикой качества всех трех видов систем распределения информации является вероятность обслуживания заявки :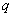

,

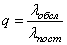или вероятность отказа в обслуживании :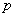

.

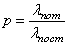Величина 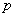получила название вероятность блокировки вызова. При этом за единицу измерения качества обслуживания принята тысячная доля единицы или промилле: .

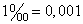Кроме потерь по вызовам существуют еще потери по нагрузке 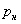и по времени 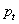. Вероятность потерь по нагрузке определяется выражением

,

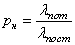а по времени

,

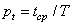где 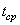- среднее время занятости каналов связи; 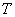- общее время работы системы распределения информации.

Для оценивания качества систем с ожиданием используется вероятность превышения времени ожидания 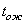заданной величине :

.

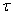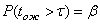Если величина 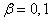, то система распределения информации имеет высокое качество обслуживания, при 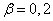- пониженное. Вероятность 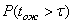рассчитывается на основе накопленной статистики: числа вызовов простоявших в очереди времени больше величины 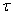и общего числа поступивших заявок:

.

12.Основные параметры и расчет интенсивности нагрузкиОсновными параметрами нагрузки являются: число источников нагрузки . n;

среднее число вызовов, поступающих от одного источника нагрузки в единицу времени, . с(штрих);

средняя длительность занятия коммутационной системы пря обслуживании одного вызова . t(штрих).

Принципы проектирования основных параметров нагрузки рассмотрим на примере их проектирования для местных телефонных сетей.

Число источников нагрузкиn. По среднему числу вызовов и средней длительности занятия на ГТС различают следующие категории источников телефонной нагрузки: телефонные аппараты народнохозяйственного сектора . n_нх; квартирные телефонные аппараты, которые делятся на квартирные аппараты индивидуального пользования . n_к.и и квартирные аппараты коллективного пользования . п_к._к; таксофоны . n_т; соединительные линии от учрежденческих телефонных станций . n_сл. Таким образом

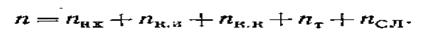
Среднее число вызовов от одного источника в единицу временис. В соответствии с имеющимися категориями источников нагрузки среднее число вызовов в единицу времени от

одного телефонного аппарата народнохозяйственного сектора обозначается через с_нх, от квартирного аппарата индивидуального пользования . c_к.и, коллективного пользования . c_к.к, от таксофона . c_т, от соединительной линии . c_сл. Обозначим в общем виде через c_i среднее число вызовов от источников i-й категории, п_i. число источников i-й категории. Тогда при k категориях источников нагрузки на АТС средневзвешенное число вызовов от одного источника определится из выражения

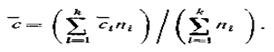
Средняя длительность занятияt. Под длительностью одного занятия понимается промежуток времени с момента снятия абонентом микротелефона (замыкание шлейфа абонентской линии) до момента возвращения приборов станции, занятых в обслуживании вызова, в исходное состояние.

Длительность занятия зависит в основном от действий абонентов и частично от систем АТС. Следовательно, длительность занятия является случайной величиной и ее среднее значение может быть определено только на основании результатов наблюдений на действующих сетях.

Разговор состоялся. Средняя длительность этого вида занятия может быть рассчитана по формуле

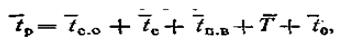
где (штрих)t_с.о, t_с, t_п.в, Т, t_o. средние продолжительности соответственно слушания абонентом сигнала ответа станции, установления соединения, посылки вызова вызываемому

абоненту, разговора, возвращения приборов в исходное состояние после отбоя.

Средняя интенсивность поступающей нагрузки.Проектирование средней интенсивности поступающей нагрузки основывается на результатах наблюдений за параметрами нагрузки на действующих АТС и предположении о тенденции изменения этих параметров с развитием ГТС.

Величина интенсивности нагрузки может быть рассчитана поформуле

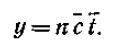
Теория телетрафика . одна из ветвей теории массового обслуживания

Количественная сторона процессов массового обслуживания является предметом раздела прикладной математики, которую советский математик А. Я. Хинчин (1894.1959 гг.) назвал теорией массового обслуживания. Родилась теория массового обслуживания в первой четверти XX века вследствие возникновения потребностей разработки математических методов для оценки качества функционирования телефонных систем. Основоположником теории телетрафика, из которой «выросла» теория массового обслуживания, является датский ученый А. К. Эрланг (1878.1929 гг.).сотрудник Копенгагенской телефонной компании.

В теории массового обслуживания все рассматриваемые объекты объединяются под общим названием «системы массового обслуживания». Одним из классов систем массового обслуживания являются системы распределения информации (системы телетрафика). Системой распределения информации могут быть совокупность коммутационных приборов, часть или весь коммутационный узел либо сеть связи, которые обслуживают по определенному алгоритму телефонные, телеграфные и другие сообщения.

В настоящее время методы теории массового обслуживания используются для решения самого широкого круга задач . от бытового обслуживания до космических исследований, однако определяющую роль в развитии теории массового обслуживания продолжает играть одна из ее ветвей . теория телетрафика.

Предметом теории телетрафика является количественная, сторона процессов обслуживания потоков сообщений в системах распределения информации.