Нахождение оценок параметров по методу моментов

Найдем сначала начальные моменты 1-го и 2-го порядка:

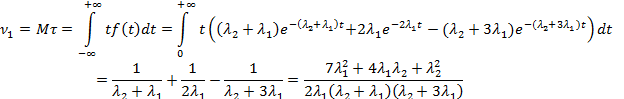
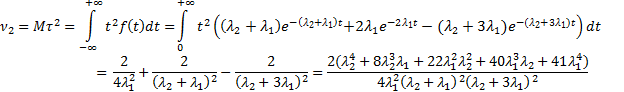
На основании группированной выборки вычислим выборочные моменты:

,

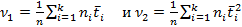где

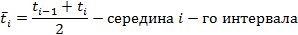
k – количество интервалов

Результаты:

k=30 n=1005 =1473 3495210

Составим систему уравнений для нахождения оценок параметров:

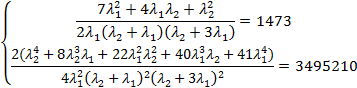
Возведя обе части первого уравнения в квадрат и разделив почленно на второе уравнение, получим:

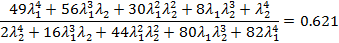
Разделим числитель и знаменатель на λ₁⁴ и, обозначив: 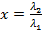- придем к уравнениючетвертой степени:

-0.242x⁴– 1.936x³+ 2.676x²+6.32x -1.922=0

Его единственный положительный корень: х ≈ 0.278

Подставим теперь λ₂=0.278∙λ₁ в первое уравнение системы:

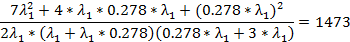
Отсюда найдем оценки параметров:

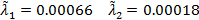
Используя найденные оценки, получим оценки функции распределения и плотности вероятности:

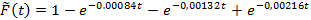(1`)

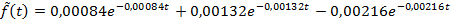(2`)

(здесь: t>0; при t≤0обе функции равны 0).

График оценки плотности вероятности и гистограмма

Для построения гистограммы найдем высоты соответствующих прямоугольников:

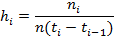
Значения h_iприведены в таблице 2.

Таблица 2 – Значения высот прямоугольников гистограммы

Номер интервала i	Высота прямоугольника hi
	2.72711*10-4
	5.12254*10-4
	4.42233*10-4
	4.90142*10-4
	3.83269*10-4
	3.50101*10-4
	2.0269*10-4
	2.39543*10-4
	1.65837*10-4
	1.36355*10-4
	1.21614*10-4
	7.37055*10-5
	7.37055*10-5
	5.89644*10-5
	3.68528*10-5
	2.57969*10-5
	4.05381*10-5
	1.84264*10-5
	2.57969*10-5
	3.68528*10-6
	7.37055*10-6
	1.10558*10-5
	3.68528*10-6
	3.6852810-6
	6.1421310-7

Соответствующие графики изображены на рисунке 2.

Рисунок 2 – График оценки вероятности и гистограмма

Оценивание функции распределения

Значение выборочной функции распределения

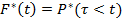
в точках t_iможно найти по формуле:

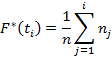
При этом: F^*(t)=0, если t ≤ 0и F^*(t)=1, если t ≥ t_k.

Эти значения, а также 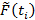приведены в таблице 3.

Соответствующие графики изображены на рисунке 3.

Таблица 3 – Значение F^*(t_i) и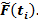

i	ti	F*(t)		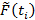i	ti	F*(t)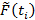
		0.07363	0.06084			0.96816	0.9702
		0.21194	0.18588			0.9791	0.97655
		0.33134	0.32415			0.98408	0.98152
		0.46368	0.45301			0.99104	0.98543
		0.56716	0.5641			0.99204	0.98849
		0.66169	0.65592			0.99403	0.9909
		0.71642	0.72994			0.99701	0.9928
		0.78109	0.7887			0.99801	0.9943
		0.82587	0.83493			0.99801	0.99548
		0.86269	0.87109			0.99801	0.99642
		0.89552	0.89929			0.99801	0.99716
		0.91542	0.92126			0.99801	0.99774
		0.93532	0.93836			0.999	0.99821
		0.95124	0.95169			0.999	0.99858
		0.96119	0.96209				0.99964

Рисунок 3 – Оценивание функции распределения

Видно, что оценка функции распределения, полученная на основе построенной математической модели с помощью метода моментов, весьма близка к выборочной функции распределения.

Проверка гипотезы о виде закона распределения

Проверяемая гипотеза H₀ состоит в том, что функция распределения времени безотказной работы рассматриваемой системы действительно задается формулой (1).

В соответствие с критерием Пирсона используем статистику

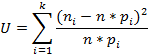
гдеp_i=F(t_i)-F(t_i-1) – вероятность попадания случайной величины τ в i – й интервал. Поскольку значения параметров неизвестны, вместо функции F(t) берется ее оценка
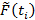Кроме того, при вычисленииp_k полагаем: p_k=1-F(t_k-1).

Зададим уровень значимости α=0.05 и будем искать критическое значение U_кр из условия:

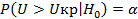
Как известно, при справедливости гипотезы H₀можно считать, что статистика U распределена по закону хи – квадрат с числом степеней свободы r= k-1-m , где m – количество оцениваемых параметров, т.е. в нашем случае r=k-3=27. Поэтому в качестве U_крвозьмем s_r,a, определяемое условием:

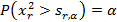
где 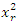- случайная величина, распределенная по закону хи – квадрат с числом степенейсвободы r.

Из таблицы распределения хи – квадрат (см. приложение Б) имеем:

U_кр =s_27,0.05>40.1.

Вычислим значение статистики U=27.702

Поскольку полученное значение U<U_кр гипотеза H₀принимается.