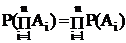Теорема сложения вероятностей

1) Для несовместных событий.

Вероятность суммы событий равна сумме вероятностей

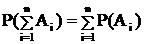
2) Вероятность полной группы событий равна 1

А, В, С… - полная группа событий.

Р(А + В + С + …) = 1

3) Для совместных событий

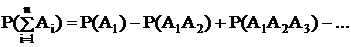
Теорема умножения вероятностей

Произведение 2-х событий обозначает, что оба эти события происходят одновременно.

1) Вероятность произведения независимых событий равна произведению их вероятностей:

2) Если события зависимые, то вероятность произведения событий равна:

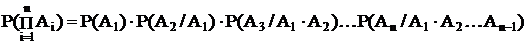
Пример 1.

Статическая вероятность повреждения каждой цепи двухцепной ЛЭП

Р*(А₁)=Р*(А₂)=10^-3

Линия обеспечивает 75% резервирования питания, т.е. одна ее цепь может покрыть 75% нагрузки приемника. Рассматривая повреждения цепей линии как независимые события вычислить вероятность полной потери питания и 25% - го дефицита мощности.

Вероятность полной потери питания (событие А)

Р*(А)=Р*(А₁)×Р*(А₂)=10^-3×10^-3=10^-6

Вероятность работы линии [Р* ]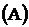

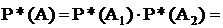(1-Р*(А₁))×(1-Р*(А₂))=(1-10^-3)×(1-10^-3)=0,999999×

0,999999

Вероятность 25%-го дефицита мощности (одна линия работает, а другая – нет и наоборот)

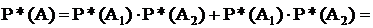2×0,999999×10^-3=0,001998

Пример №2

Статическая вероятность однополюсного замыкания воздушных линий равна 10^-3 (Р*(А)=10^-3)

При в озникновении однополюсного замыкания за счет повышения напряжения на здоровых фазах а также за счет ионизации воздуха вероятность повреждения здоровых фаз увеличивается, т.е. эти события зависимые.

Условная вероятность короткого замыкания другой фазы равна 0,2.

Р*(В/А)=0,2.

Условная вероятность короткого замыкания 3-й фазы при повреждении 2-ух других

Р*(С/ВА)=0,5

(А, В, С не фазы, а случайные события)

Определить вероятность 2-х полюсного и 3-х полюсного к.з. линий.

Вероятность 2-х полюсного к.з.:

Р*(Д)=Р*(А)×Р*(В/А)=10^-3×0,2=2×10^-4

3-х полюсного к.з.:

Р*(F)=P*(A)×P*(B/A)×P*(C/BA)=10^-3×0,2×0,5=1×10^-4=10^-4

Пример №3

Энергетический блок представляет собой последовательное соединение парового котла, паровой турбины и электрического генератора (паровая турбина получает весь пар от котла, а генератор расположен на одном валу с турбиной).

Вероятность повреждения отдельных отдельных элементов блока соответствует для котла, турбины, генератора:

Р_к=0,02; Р_т=0,01; Р_г=0,01

Определить вероятность повреждения электрического блока.

Р_б-?

Вероятность работы блока:

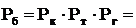(1-0,02)(1-0,01)(1-0,01)=0,98×0,99×0,99=0,97

Вероятность выхода блока из строя

Р_б=1- 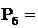1-0,97=0,039

Формула полной вероятности

Определим вероятность события А, которое может произойти одновременно с событием (одним из них) В₁, В₂…В_n, которые составляют полную группу несовместимых событий, их называют гипотезами.

А=АВ₁+АВ₂+…+АВ_n

Р(А)=р(АВ₁)+р(АВ₂)+…+р(АВ_n)

А и В₁, В₂…В_n зависимые

Р(А)=р(В₁)×р(А/В₁)+р(В₂)×р(А/В₂)+…+р(В_n)×p(A/B_n)

Формула полной вероятности:

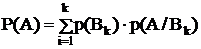
Пример 1

Статическая вероятность повреждения изоляции в нормальном режиме системы с малым током замыкания на землю равна Р*(А/В₁)=0,001

При замыкании фазы системы на землю вероятность повреждения изоляции трансформатора равна

Р*(А/В₂)=0,005

Как показали наблюдения работа с заземленной фазой системы длится в среднем 100 часов в год.

Найти полную вероятность повреждения трансформатора.

Решение:

Вероятность работы трансформатора с заземленной фазой:

Р*(В₂)=M/N=100/8760=0,0114

Р*(В₁) - вероятность нормальной работы системы.

Р*(В₁)=1-Р*(В₂)=1-0,0114=0,9986

Р*(А)=Р*(В₁)×Р*(А/В₁)+Р*(В₂)×Р(А/В₂)=0,9986×0,001+0,0114×0,005=0,0010456

Теорема Байеса

Если известны вероятности, гипотезы события несовместны

В₁, В₂, В₃…В_n – гипотезы

Р(В₁), Р(В₂), … Р(В_n) – известны

В результате опытов может произойти событие А. Нас интересует вероятность появления какой-либо из гипотез после того, как произошло событие А:

Р(В_к/А)-?

Р(А×В_к)=Р(А)×Р(В_к/А)=Р(В_к)×Р(А/В_к)

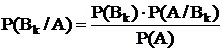
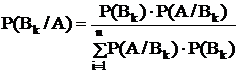
Теорема дает возможность определить условие вероятности гипотезы, если известна вероятность гипотез до опыта и условная вероятность появления события А при этих гипотезах.

Пример:

Две электростанции работают на общую нагрузку. Покрытие нагрузки возможно только при одновременной работе обеих электростанций. Надежность (вероятность безотказной работы на протяжении времени t):

1-й электростанции: Р*(С₁)=0,96

2-й электростанции: Р*(С₂)=0,94

Система работала на протяжении времени t. При этом приемник один раз потерял электроснабжение. Найти вероятность того, что вышла из строя только 1-я электростанция, а другая осталась исправной.

Возможны 4 гипотезы:

В_о – обе электростанции исправны;

В₁ – одна - неисправна, другая – исправна;

В₂ – наоборот;

В₃ – обе неисправны.

Р(В_о) = р*(С₁)×р*(С₂)

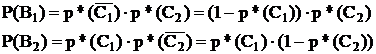
Р(В₃) = (1-р*(С₁))×(1-р*(С₂))

Р(А/В_о) = 0

Р(А/В₁) = Р(А/В₂) = Р(А/В₃) = 1

=

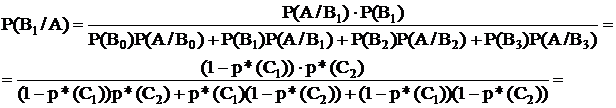
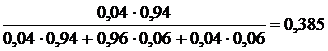
Фильтрация спама по Байесу

Наверное, каждый пользователь, активно пользующийся электронной почтой и "живущий" в интернете несколько лет, сталкивается с проблемой нежелательных массовых рассылок (спама). Особенно если его использует свой адрес для подписки на публичные дискуссионные листы, или опубликовал его в октрытом виде на каком-нибудь сайте или доске объявлений...

Поначалу спам не вызывает никаких проблем, кроме лёгкой досады. Однако с увеличением количества подобных писем даже элементарная операция сортировки почты на "нужное" и "мусор" начинает занимать непозволительно много времени, не говоря уже о том, что весь мусор приходится, к тому же, скачивать из интернета.

В ответ на возникающий в такой ситуации вопрос: "Что делать?", — в интернете в настоящий момент можно найти довольно большое количество всевозможных фильтров, защищающих почтовый ящик от мусора. Принципы их работы самые разные. Простейшие содержат некоторую базу "запрещённых" и "разрешённых" слов или фраз, при наличии которых входящее письмо может либо беспрепятственно попасть в ящик, либо же быть безжалостно удалённым ещё на "входе". К одному из вариантов подобной фильтрации относится, в частности, фильтрация по публичным smtp-серверам, которые используют спамеры для своих рассылок. Другой метод блокировки — отправлять в ответ на каждое письмо запрос на подтверждение, в расчёте на то, что хороший человек на него непременно ответит, а спамеры — проигнорируют.

Недостатки обоих перечисленных методов очевидны: в первом случае используется база слов, которую тоже кто-то должен составлять. Из-за этого по иронии судьбы смысл работы фильтра меняется на противоположный: вместо того, чтобы избавиться от чтения спама, вам как раз приходится читать и анализировать его, пытаясь выявить очередные примечательные слова, которыми можно пополнить базу данных фильтра. Но даже в этом случае, спамеру достаточно в очередной раз написать в письме вместо "корова" -> "карова", чтобы его письмо снова беспрепятственно оказалось в вашем ящике.

Второй случай, с запросом на подтверждение, опять же, неудобен обычным отправителям, которым приходится фактически отправлять вам два письма — "информационное" и "утвердительное". К тому же слабым местом подобного метода является допущение, что спамер ни в коем случае не будет подтверждать намерение попасть к вам в ящик, а также то, что обратный адрес спамерского письма всегда фиктивен. Оба утверждения, как показывает практика, весьма неоднозначны. Обратный адрес может быть не выдуманным, а случайно или специально совпасть с адресом существующего человека. Тогда он, скорее всего, ради любопытства ответит на пришедшее непонятно откуда письмо-подверждение — и тем самым письмо спамера будет доставлено до адресата, а сам он, ничего не подозревая, может запросто попасть в чей-нибудь "чёрный список". Вероятность такого невольного ответа довольно велика: если пользователь, чей адрес подставлен вместо обратного, активно пользуется почтой, он может просто автоматически подтвердить доставку, не разбираясь, что это за письмо. Если же пользователь неопытен, то он просто нажмёт "ответить", ради любопытства... Опять же, далеко не все почтовые сервера корректно рапортуют о недоставленной почте. Корректно - в смысле, что исходное письмо прилагается в виде вложения, а текст отчёта содержит только техническую информацию о нём. Бывает, что сервер просто отсылает письмо назад в неизменном виде - а это значит, что если это было письмо-запрос на подтверждение, то программа-фильтр вполне может принять его именно за корректное подтверждение доставки. Наконец, если игра будет стоит свеч, то вполне могут появиться программы массовой рассылки, которые будет отправлять подобные подтверждения, — и метод "свой-чужой" потеряет свои плюсы.

Практически всё множество существующих на данный момент антиспамерских фильтров базируются на этих двух перечисленных принципах. Отличаются же они, как правило, "мощностью" спамерской базы, а также регулярностью и степенью её обновления.

Как правило антиспамерские фильтры выполняются либо как службы-демоны (daemon) на почтовом сервере, либо же как служебные программы на клиентских рабочих станциях, "висящие" где-нибудь в памяти компьютера, и, естественно, забирающие на себя определённую часть его ресурсов. Если спамерская база подобных фильтров пополняется через интернет, то эта программа будет расходовать также определённую часть сетевого трафика.

Ещё одним существенным недостатком многих антиспамерских фильтров является их ориентация "на запад". Наш же, "отечественный" спам проходит подобные "заграждения" довольно легко. Спамеры ведь тоже не стоят на месте: они так же пользуются всеми подобными фильтрами, тестируя свою рассылку, чтобы максимально эффективно обмануть все заграждения. И, надо сказать, что возможностей для этого у русского спамера заметно больше, чем у иностранца. Ведь кроме упомянутой "каровы" можно написать "kopoвa", почти по-английски, заменив (в данном случае) большинство русских букв на аналогично выглядящие латинские. И такое слово с большой вероятностью пройдёт практически через любой "западный" фильтр (одна западная антиспамерская компания даже организовала целую лабораторию по борьбе со спамом из России. Причина - упомянутое "частичное транслитерирование").

В общем, битва назойливых спамеров и их адресатов продолжается...

The Bat! и антиспамерские фильтры

Вряд ли имеет смысл на официальном сайте рассказывать, что такое The Bat!, поэтому сразу перейду к делу.

Начиная с версии 1.63 The Bat! предоставил пользователям возможность подключать и использовать антиспаммерские фильтры. Фильтр работает во время получения почты и оценивает каждое входящее письмо по шкале от 0 до 100. 0 означает, что письмо "хорошее", 100 — что это спам. Затем уже сам The Bat! может на основании этой оценки что-нибудь сделать с письмом — например, удалить спам или поместить его в специальную папку "макулатура".

Главное достоинство этой технологии в том, что фильтр в контексте The Bat! уже не является самостоятельным сервисом, живущим где-нибудь в трее или в недрах компьютера, но представляет собой подключаемую библиотеку, которая загружается только при работе с почтой, а затем автоматически выгружается, не занимая памяти или других ресурсов. Опять же, поскольку письмо "доставляется" фильтру непосредственно средствами The Bat!, то возможна работа со всеми видами почтовых протоколов, поддерживаемых этой программой, вплоть до "локальной доставки", когда письмо доставляется из одного ящика в другой, расположенный на этом же компьютере, без задействования в этом процессе сетевого трафика.

Итак, антиспамерские фильтры The Bat! потенциально не нуждаются в том, чтобы быть постоянно запущенными как сервис, и также не нуждаются в использовании сети.

Осталось только найти подходящий фильтр...