Оценка уровней значимости коэффициентов регрессионного уравнения

Для коэффициентов регрессионного уравнения проверка их уровня значимости осуществляется по t-критерию Стьюдента и по критерию FФишера. Ниже мы рассмотрим оценку достоверности показателей регрессии только для линейных уравнений (12.1) и (12.2).

Y=a 0 + a1 X (12.1)

Х= b 0 + b1 Y (12.2)

Для это типа уравнений оценивают по t-критерию Стьюдента только величины коэффициентов а1и b1с использованием вычисления величины Тф по следующим формулам:

где

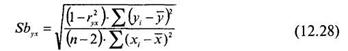
Где r_yx коэффициент корреляции, а величину а1можно вычислить по формулам 12.5 или 12.7.

Формула (12.27) используется для вычисления величины Тф, которая позволяет оценить уровень значимости коэффициента а1уравнения регрессии Y по X.

Где

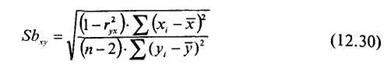
Величину b1можно вычислить по формулам (12.6) или (12.8).

Формула (12.29) используется для вычисления величины Тф, которая позволяет оценить уровень значимости коэффициента b1уравнения регрессии X по Y

Пример.Оценим уровень значимости коэффициентов регрессии а1и b1уравнений (12.17), и (12.18), полученных при решении задачи 12.1. Воспользуемся для этого формулами (12.27), (12.28), (12.29) и (12.30).

Напомним вид полученных уравнений регрессии:

Y_х = 3 + 0,06 • X (12.17)

X_y = 9+1 • Y (12.19)

Величина а1в уравнении (12.17) равна 0,06. Поэтому для расчета по формуле (12.27) нужно подсчитать величину Sb_yх. Согласно условию задачи величина п = 8. Коэффициент корреляции также уже был подсчитан нами по формуле 12.9: r_xy = √0,06 •0,997 = 0,244 .

Осталось вычислить величины Σ (у_ι - y)²и Σ(х_ι –x)², которые у нас не подсчитаны. Лучше всего эти расчеты проделать в таблице 12.2:

Таблица 12.2

№ испыту­емых п/п	хι	уi	хι –x	(хι –x)2	уι - y	(уι - y)2
			-4,75	22,56	- 1,75	3,06
			-4,75	22,56	-0,75	0,56
			-2,75	7,56	0,25	0,06
			-2,75	7,56	1,25	15,62
			1,25	1,56	1,25	15,62
			3,25	10,56	0,25	0,06
			5,25	27,56	-0,75	0,56
			5,25	27,56	0,25	0,06
Суммы				127,48		35,6
Средние	12,75	3,75

Подставляем полученные значения в формулу (12.28), получаем:

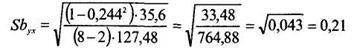
Теперь рассчитаем величину Тф по формуле (12.27):

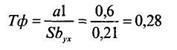
Величина Тф проверяется на уровень значимости по таблице 16 Приложения 1 для t-критерия Стьюдента. Число степеней свободы в этом случае будет равно 8-2 = 6, поэтому критические значения равны соответственно для Р ≤0,05 t_кр = 2,45 и для Р≤ 0,01 t_кр =3,71. В принятой форме записи это выглядит так:

Строим «ось значимости»:

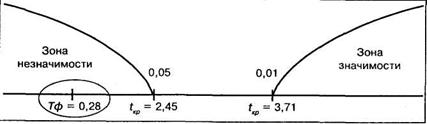
Полученная величина Тф попала в зону незначимости, следовательно мы должны принять гипотезу Н_о о том, что величина коэффициента регрессии уравнения (12.17) неотличима от нуля. Иными словами, полученное уравнение регрессии неадекватно исходным экспериментальным данным.

Рассчитаем теперь уровень значимости коэффициента b1. Для этого необходимо вычислить величину Sb_xy по формуле (12.30), для которой уже расчитаны все необходимые величины:

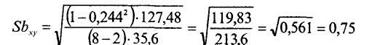
Теперь рассчитаем величину Тф по формуле (12.27):

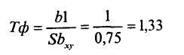
Мы можем сразу построить «ось значимости», поскольку все предварительные операции были проделаны выше:

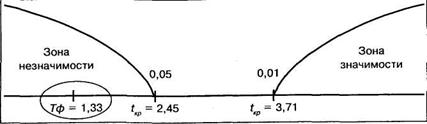
Полученная величина Тф попала в зону незначимости, следовательно мы должны принять гипотезу H_о о том, что величина коэффициента регрессии уравнения (12.19) неотличима от нуля. Иными словами, полученное уравнение регрессии неадекватно исходным экспериментальным данным.

Нелинейная регрессия

Полученный в предыдущем разделе результат несколько обескураживает: мы получили, что оба уравнения регрессии (12.15) и (12.17) неадекватны экспериментальным данным. Последнее произошло потому, что оба эти уравнения характеризуют линейную связь между признаками, а мы в разделе 11.9 показали, что между переменными X и Y имеется значимая криволинейная зависимость. Иными словами, между переменными Х и Y в этой задаче необходимо искать не линейные, а криволинейные связи. Проделаем это с использованием пакета «Стадия 6.0» (разработка А.П. Кулаичева, регистрационный номер 1205).

Задача 12.2. Психолог хочет подобрать регрессионную модель, адекватную экспериментальным данным, полученным в задаче 11.9.

Решение.Эта задача решается простым перебором моделей криволинейной регрессии предлагаемых в статистическом пакете Стадия. Пакет организован таким образом, что в электронную таблицу, которая является исходной для дальнейшей работы, заносятся экспериментальные данные в виде первого столбца для переменной X и второго столбца для переменной Y. Затем в основном меню выбирается раздел Статистики, в нем подраздел — регрессионный анализ, в этом подразделе вновь подраздел — криволинейная регрессия. В последнем меню даны формулы (модели) различных видов криволинейной регрессии, согласно которым можно вычислять соответствующие регрессионные коэффициенты и сразу же проверять их на значимость. Ниже рассмотрим только несколько примеров работы с готовыми моделями (формулами) криволинейной регрессии.

1. Первая модель — экспонента. Ее формула такова:

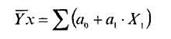
При расчете с помощью статпакета получаем а₀ = 1 и а₁= 0,022.

Расчет уровня значимости для а, дал величину Р = 0,535. Очевидно, что полученная величина незначима. Следовательно, данная регрессионная модель неадекватна экспериментальным данным.

2. Вторая модель — степенная. Ее формула такова:

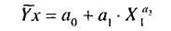
При подсчете а_о = - 5,29, а, = 7,02 и а₁= 0,0987.

Уровень значимости для а₁ — Р = 7,02 и для а₂ — Р = 0,991. Очевидно, что ни один из коэффициентов не значим.

Вывод — данная модель неадекватна экспериментальным данным.

3. Третья модель — полином. Ее формула такова:

Y = а₀ + а₁ • X + а₂ • X² + а₃ • X³

При подсчете а₀ = - 29,8, а₁ = 7,28, а₂ = - 0,488 и а₃ = 0,0103. Уровень значимости для а, — Р = 0,143, для а₂ — Р = 0,2 и для а, — Р= 0,272

Вывод — данная модель неадекватна экспериментальным данным.

4. Четвертая модель — парабола.

Ее формула такова: Y= a_o + a_l-X¹ + а₂Х²

При подсчете а₀ = - 9,88, а, = 2,24 и а₁ = - 0,0839 Уровень значимости для а₁ — Р = 0,0186, для а₂ — Р = 0,0201. Оба регрессионных коэффициента оказались значимыми. Следовательно, задача решена — мы выявили форму криволинейной зависимости между успешностью решения третьего субтеста Векслера и уровнем знаний по алгебре — это зависимость параболического вида. Этот результат подтверждает вывод, полученный при решении задачи 11.9 о наличии криволинейной зависимости между переменными. Подчеркнем, что именно с помощью криволинейной регрессии был получен точный вид зависимости между изучаемыми переменными.

.

Глава 13 ФАКТОРНЫЙ АНАЛИЗ

Основные понятия факторного анализа

Факторный анализ — статистический метод, который используется при обработке больших массивов экспериментальных данных. Задачами факторного анализа являются: сокращение числа переменных (редукция данных) и определение структуры взаимосвязей между переменными, т.е. классификация переменных, поэтому факторный анализ используется как метод сокращения данных или как метод структурной классификации.

Важное отличие факторного анализа от всех описанных выше методов заключается в том, что его нельзя применять для обработки первичных, или, как говорят, «сырых», экспериментальных данных, т.е. полученных непосредственно при обследовании испытуемых. Материалом для факторного анализа служат корреляционные связи, а точнее — коэффициенты корреляции Пирсона, которые вычисляются между переменными (т.е. психологическими признаками), включенными в обследование. Иными словами, факторному анализу подвергают корреляционные матрицы, или, как их иначе называют, матрицы интеркорреляций. Наименования столбцов и строк в этих матрицах одинаковы, так как они представляют собой перечень переменных, включенных в анализ. По этой причине матрицы интеркорреляций всегда квадратные, т.е. число строк в них равно числу столбцов, и симметричные, т.е. на симметричных местах относительно главной диагонали стоят одни и те же коэффициенты корреляции.

Необходимо подчеркнуть, что исходная таблица данных, из которой получается корреляционная матрица, не обязательно должна быть квадратной. Например, психолог измерил три показателя интеллекта (вербальный, невербальный и общий) и школьные отметки по трем учебным предметам (литература, математика, физика) у 100 испытуемых — учащихся девятых классов. Исходная матрица данных будет иметь размер 100 × 6, а матрица интеркорреляций размер 6 × 6, поскольку в ней имеется только 6 переменных. При таком количестве переменных матрица интеркорреляций будет включать 15 коэффициентов и проанализировать ее не составит труда.

Однако представим, что произойдет, если психолог получит не 6, а 100 показателей от каждого испытуемого. В этом случае он должен будет анализировать 4950 коэффициентов корреляции. Число коэффициентов в матрице вычисляется по формуле n•(n+1)/2 и в нашем случае равно соответственно (100×99)/2= 4950.

Очевидно, что провести визуальный анализ такой матрицы — задача труднореализуемая. Вместо этого психолог может выполнить математическую процедуру факторного анализа корреляционной матрицы размером 100 × 100 (100 испытуемых и 100 переменных) и таким путем получить более простой материал для интерпретации экспериментальных результатов.

Главное понятие факторного анализа — фактор.Это искусственный статистический показатель, возникающий в результате специальных преобразований таблицы коэффициентов корреляции между изучаемыми психологическими признаками, или матрицы интеркорреляций. Процедура извлечения факторов из матрицы интеркорреляций называется факторизацией матрицы. В результате факторизации из корреляционной матрицы может быть извлечено разное количество факторов вплоть до числа, равного количеству исходных переменных. Однако факторы, выделяемые в результате факторизации, как правило, неравноценны по своему значению.

Элементы факторной матрицы называются «факторными нагрузками, или весами»; и они представляют собой коэффициенты корреляции данного фактора со всеми показателями, использованными в исследовании. Факторная матрица очень важна, поскольку она показывает, как изучаемые показатели связаны с каждым выделенным фактором. При этом факторный вес демонстрирует меру, или тесноту, этой связи.

Поскольку каждый столбец факторной матрицы (фактор) является своего рода переменной величиной, то сами факторы также могут коррелировать между собой. Здесь возможны два случая: корреляция между факторами равна нулю, в таком случае факторы являются независимыми (ортогональными). Если корреляция между факторами больше нуля, то в таком случае факторы считаются зависимыми (облическими). Подчеркнем, что ортогональные факторы в отличие от облических дают более простые варианты взаимодействий внутри факторной матрицы.

В качестве иллюстрации ортогональных факторов часто приводят задачу Л. Терстоуна, который, взяв ряд коробок разных размеров и формы, измерил в каждой из них больше 20 различных показателей и вычислил корреляции между ними. Профакторизовав полученную матрицу интеркорреляций, он получил три фактора, корреляция между которыми была равна нулю. Этими факторами были «длина», «ширина» и «высота».

Для того чтобы лучше уловить сущность факторного анализа, разберем более подробно следующий пример.

Предположим, что психолог у случайной выборки студентов получает следующие данные:

• V₁ — вес тела (в кг);

• V₂ — количество посещений лекций и семинарских занятий по предмету;

• V₃— длина ноги (в см);

• V₄ — количество прочитанных книг по предмету;

• V₅ — длина руки (в см);

• V₆ — экзаменационная оценка по предмету (V— от английского слова variable — переменная).

При анализе этих признаков не лишено оснований предположение о том, что переменные V₁, К₃ и V₅ — будут связаны между собой, поскольку, чем больше человек, тем больше он весит и тем длиннее его конечности. Сказанное означает, что между этими переменными должны получиться статистически значимые коэффициенты корреляции, поскольку эти три переменные измеряют некоторое фундаментальное свойство индивидуумов в выборке, а именно: их размеры. Точно так же вероятно, что при вычислении корреляций между V₂, V₄ и V₆ тоже будут получены достаточно высокие коэффициенты корреляции, поскольку посещение лекций и самостоятельные занятия будут способствовать получению более высоких оценок по изучаемому предмету.

Таким образом, из всего возможного массива коэффициентов, который получается путем перебора пар коррелируемых признаков V₁ и V₂, V_t и V₃ и т.д., предположительно выделятся два блока статистически значимых корреляций. Остальная часть корреляций — между признаками, входящими в разные блоки, вряд ли будет иметь статистически значимые коэффициенты, поскольку связи между такими признаками, как размер конечности и успеваемость по предмету, имеют, скорее всего, случайный характер. Итак, содержательный анализ 6 наших переменных показывает, что они, по сути дела, измеряют только две обобщенные характеристики, а именно: размеры тела и степень подготовленности по предмету.

К полученной матрице интеркорреляций, т.е. вычисленным попарно коэффициентам корреляций между всеми шестью переменными V₁ - V₆, допустимо применить факторный анализ. Его можно проводить и вручную, с помощью калькулятора, однако процедура подобной статистической обработки очень трудоемка. По этой причине в настоящее время факторный анализ проводится на компьютерах, как правило, с помощью стандартных статистических пакетов. Во всех современных статистических пакетах есть программы для корреляционного и факторного анализов. Компьютерная программа по факторному анализу по существу пытается «объяснить» корреляции между переменными в терминах небольшого числа факторов (в нашем примере двух).

Предположим, что, используя компьютерную программу, мы получили матрицу интеркорреляций всех шести переменных и подвергли ее факторному анализу. В результате факторного анализа получилась таблица 13.1, которую называют «факторной матрицей», или «факторной структурной матрицей».

Таблица 13.1

Переменная	Фактор 1	Фактор 2
V1	0,91	0,01
V2	0,20	0,96
V3	0,94	-0,15
V4	0,11	0,85
V5	0,89	0,07
V6	-0,13	0,93

По традиции факторы представляются в таблице в виде столбцов, а переменные в виде строк. Заголовки столбцов таблицы 13.1 соответствуют номерам выделенных факторов, но более точно было бы их называть «факторные нагрузки», или «веса», по фактору 1, то же самое по фактору 2. Как указывалось выше, факторные нагрузки, или веса, представляют собой корреляции между соответствующей переменной и данным фактором. Например, первое число 0,91 в первом факторе означает, что корреляция между первым фактором и переменной V₁ равна 0,91. Чем выше факторная нагрузка по абсолютной величине, тем больше ее связь с фактором.

Из таблицы 13.1 видно, что переменные V₁ V₃ и V₅ имеют большие корреляции с фактором 1 (фактически переменная 3 имеет корреляцию близкую к 1 с фактором 1). В то же время переменные V₂, V₃ и У₅ имеют корреляции близкие к 0 с фактором 2. Подобно этому фактор 2 высоко коррелирует с переменными V₂, V₄ и V₆ и фактически не коррелирует с переменными V₁, V₃ и V₅

В данном примере, очевидно, что существуют две структуры корреляций, и, следовательно, вся информация таблицы 13.1 определяется двумя факторами. Теперь начинается заключительный этап работы — интерпретация полученных данных. Анализируя факторную матрицу, очень важно учитывать знаки факторных нагрузок в каждом факторе. Если в одном и том же факторе встречаются нагрузки с противоположными знаками, это означает, что между переменными, имеющими противоположные знаки, существует обратно пропорциональная зависимость.

Отметим, что при интерпретации фактора для удобства можно изменить знаки всех нагрузок по данному фактору на противоположные.

Факторная матрица показывает также, какие переменные образуют каждый фактор. Это связано, прежде всего, с уровнем значимости факторного веса. По традиции минимальный уровень значимости коэффициентов корреляции в факторном анализе берется равным 0,4 или даже 0,3 (по абсолютной величине), поскольку нет специальных таблиц, по которым можно было бы определить критические значения для уровня значимости в факторной матрице. Следовательно, самый простой способ увидеть какие переменные «принадлежат» фактору – это значит отметить те из них, которые имеют нагрузки выше, чем 0,4 (или меньше чем - 0,4). Укажем, что в компьютерных пакетах иногда уровень значимости факторного веса определяется самой программой и устанавливается на более высоком уровне, например 0,7.

Так, из таблицы 13.1, следует вывод, что фактор 1 — это сочетание переменных V₁ К₃ и V₅ (но не V₁, K₄ и V₆, поскольку их факторные нагрузки по модулю меньше чем 0,4). Подобно этому фактор 2 представляет собой сочетание переменных V₂, V₄ и V₆.

Выделенный в результате факторизации фактор представляет собой совокупность тех переменных из числа включенных в анализ, которые имеют значимые нагрузки. Нередко случается, однако, что в фактор входит только одна переменная со значимым факторным весом, а остальные имеют незначимую факторную нагрузку. В этом случае фактор будет определяться по названию единственной значимой переменной.

В сущности, фактор можно рассматривать как искусственную «единицу» группировки переменных (признаков) на основе имеющихся между ними связей. Эта единица является условной, потому что, изменив определенные условия процедуры факторизации матрицы интеркорреляций, можно получить иную факторную матрицу (структуру). В новой матрице может оказаться иным распределение переменных по факторам и их факторные нагрузки.

В связи с этим в факторном анализе существует понятие «простая структура». Простой называют структуру факторной матрицы, в которой каждая переменная имеет значимые нагрузки только по одному из факторов, а сами факторы ортогональны, т.е. не зависят друг от друга. В нашем примере два общих фактора независимы. Факторная матрица с простой структурой позволяет провести интерпретацию полученного результата и дать наименование каждому фактору. В нашем случае фактор первый — «размеры тела», фактор второй — «уровень подготовленности».

Сказанное выше не исчерпывает содержательных возможностей факторной матрицы. Из нее можно извлечь дополнительные характеристики, позволяющие более детально исследовать связи переменных и факторов. Эти характеристики называются «общность» и «собственное значение» фактора.

Однако, прежде чем представить их описание, укажем на одно принципиально важное свойство коэффициента корреляции, благодаря которому получают эти характеристики. Коэффициент корреляции, возведенный в квадрат (т.е. помноженный сам на себя), показывает, какая часть дисперсии (вариативности) признака является общей для двух переменных, или, говоря проще, насколько сильно эти переменные перекрываются. Так, например, две переменные с корреляцией 0,9 перекрываются со степенью 0,9 х 0,9 = 0,81. Это означает, что 81% дисперсии той и другой переменной являются общими, т.е. совпадают. Напомним, что факторные нагрузки в факторной матрице — это коэффициенты корреляции между факторами и переменными, поэтому, возведенная в квадрат факторная нагрузка характеризует степень общности (или перекрытия) дисперсий данной переменной и данного фактором.

Если полученные факторы не зависят друг от друга («ортогональное» решение), по весам факторной матрицы можно определить, какая часть дисперсии является общей для переменной и фактора. Вычислить, какая часть вариативности каждой переменной совпадает с вариативностью факторов, можно простым суммированием квадратов факторных нагрузок по всем факторам. Из таблицы 13.1, например, следует, что 0,91 × 0,91 + + 0,01 × 0,01 = 0,8282, т.е. около 82% вариативности первой переменной «объясняется» двумя первыми факторами. Полученная величина называется общностью переменной, в данном случае переменной V₁

Переменные могут иметь разную степень общности с факторами. Переменная с большей общностью имеет значительную степень перекрытия (большую долю дисперсии) с одним или несколькими факторами. Низкая общность подразумевает, что все корреляции между переменными и факторами невелики. Это означает, что ни один из факторов не имеет совпадающей доли вариативности с данной переменной. Низкая общность может свидетельствовать о том, что переменная измеряет нечто качественно отличающееся от других переменных, включенных в анализ. Например, одна переменная, связанная с оценкой мотивации среди заданий, оценивающих способности, будет иметь общность с факторами способностей близкую к нулю.

Малая общность может также означать, что определенное задание испытывает на себе сильное влияние ошибки измерения или крайне сложно для испытуемого. Возможно, напротив, также, что задание настолько просто, что каждый испытуемый дает на него правильный ответ, или задание настолько нечетко по содержанию, что испытуемый не понимает суть вопроса. Таким образом, низкая общность подразумевает, что данная переменная не совмещается с факторами по одной из причин: либо переменная измеряет другое понятие, либо переменная имеет большую ошибку измерения, либо существуют искажающие дисперсию признака различия между испытуемыми в вариантах ответа на это задание.

Наконец, с помощью такой характеристики, как собственное значение фактора, можно определить относительную значимость каждого из выделенных факторов. Для этого надо вычислить, какую часть дисперсии (вариативности) объясняет каждый фактор. Тот фактор, который объясняет 45% дисперсии (перекрытия) между переменными в исходной корреляционной матрице, очевидно, является более значимым, чем другой, который объясняет только 25% дисперсии. Эти рассуждения, однако, допустимы, если факторы ортогональны, иначе говоря, не зависят друг от друга.

Для того чтобы вычислить собственное значение фактора, нужно возвести в квадрат факторные нагрузки, и сложить их по столбцу. Используя данные таблицы 13.1 можно убедиться, что собственное значение фактора 1 составляет (0,91 × 0,91 + 0,20 × 0,20 + 0,94 × 0,94 + 0,11 × 0,11 + 0,84 × 0,84 + (- 0,13) ×

× (-0,13)) = 2,4863. Если собственное значение фактора разделить на число переменных (6 в нашем примере), то полученное число покажет, какая доля дисперсии объясняется данным фактором. В нашем случае получится 2,4863∙100%/6 = 41,4%. Иными словами, фактор 1 объясняет около 41% информации (дисперсии) в исходной корреляционной матрице. Аналогичный подсчет для второго фактора даст 41,5%. В сумме это будет составлять 82,9%.

Таким образом, два общих фактора, будучи объединены, объясняют только 82,9% дисперсии показателей исходной корреляционной матрицы. Что случилось с «оставшимися» 17,1%? Дело в том, что, рассматривая корреляции между 6 переменными, мы отмечали, что корреляции распадаются на два отдельных блока, и поэтому решили, что логично анализировать материал в понятиях двух факторов, а не 6, как и количество исходных переменных. Другими словами, число конструктов, необходимых, чтобы описать данные, уменьшилось с 6 (число переменных) до 2 (число общих факторов). В результате факторизации часть информации в исходной корреляционной матрице была принесена в жертву построению двухфакторной модели. Единственным условием, при котором информация не утрачивается, было бы рассмотрение шестифакторной модели.