Проверка правильности ранжирования

Процедура ранжирования достаточно проста, однако ошибки могут возникнуть совершенно неожиданно. Поэтому всегда, когда проводится ранжирование, необходима проверка правильности реализации этой процедуры. В наиболее общем случае для проверки правильности ранжирования столбца (или строчки) признаков применяется следующая формула:

Если ранжируется N признаков, то сумма всех полученных рангов должна быть равна:

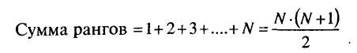
(1.1)

где N — количество ранжируемых признаков.

Эта формула широко используется в дальнейшем, поэтому ее следует хорошо запомнить.

Совпадение итогов подсчета рангов по формуле (1.1) и по реальным результатам ранжирования экспериментальных данных является подтверждением правильности ранжирования.

В случае примера 1 число ранжируемых признаков было N=7, поэтому сумма рангов, подсчитанная по формуле (1.1) должна равняться 7*8/ 2= 28.

Сложим величины рангов отдельно для левого и правого столбца таблицы 1.2:

7 + 1 + 3 + 2 + 5 + 4 + 6 = 28— для левого столбца и

1 + 5 + 7 + 6 + 4 + 3 + 2 = 28 — для правого столбца.

Суммы рангов, подсчитанные по формуле (1.1) и в результате реального ранжирования, совпали, следовательно, ранжирование проведено правильно. Подобную проверку следует обязательно делать после каждого ранжирования.

В дальнейшем нам встретиться еще несколько разных вариантов ранжирования. Например, ранжирование таблицы чисел. Подобные таблицы будут в дальнейшем использоваться достаточно часто, поэтому следует хорошо усвоить правила проверки правильности ранжирования табличных данных.

1 Вариант.Предположим, что у нас были протестированы две группы испытуемых по 5 человек в каждой группе по методике дифференциальной диагностики депрессивных состояний В.А. Жмурова и у них получены следующие тестовые баллы, которые сразу же занесем в таблицу 1.3:

Таблица 1.3

№ испытуемых п/п	Группа 1	Группа 2

Перед психологом стоит задача: проранжировать обе группы испытуемых как одну, т.е. объединить выборку и проставить ранги объединенной выборке. Сделаем это в таблице 1.4:

Таблица 1.4

№ испытуемых п/п	Группа 1	Ранги	Группа 2	Ранги
Суммы

Проверим правильность ранжирования. Поскольку у нас уже получены суммы рангов по столбцам, то общую реальную сумму рангов можно получить просто сложив эти суммы, итак 31 + 24 = 55.

Чтобы применить формулу (1.1) нужно подсчитать общее количество испытуемых — это 5 + 5 = 10, тогда по формуле (1.1) получаем: 11∙10/5=55

Следовательно, ранжирование проведено правильно.

В том случае, если в таблице имеется большое количество строк и столбцов, для подсчета рангов можно использовать модификацию формулы (1.1), она будет выглядеть так:

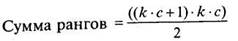
(1.2)

где k — число строк, с — число столбцов.

Проведем вычисление суммы рангов по формуле (1.2) для нашего примера. У нас 5 строк и 2 столбца, следовательно, сумма рангов будет равна

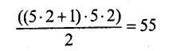
2 Вариант.В ряде статистических методов ранжирование табличных данных осуществляется по каждой строчке отдельно. Проиллюстрируем это положение на предыдущем примере, добавив еще одну группу испытуемых из 5 человек. Получится таблица 1.5 в которой проведем ранжирование по строчкам:

Таблица 1.5

№ испытуемых п/п	Группа 1	Ранги	Группа 2	Ранги	Группа 3	Ранги
Суммы

Обратите внимание, что в таблице 1.5 минимальному по величине числу ставится минимальный ранг.

В случае такого ранжирования сумма всех рангов по каждой строчке должна быть равна 6, поскольку у нас ранжируется всего три величины:

1 + 2 + 3 = 6.

Расчетная формула общей суммы рангов для такого способа ранжирования определяется по формуле:

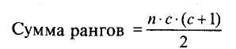(1.3)

Где п — количество испытуемых в столбце

с — количество столбцов (групп испытуемых, измерений и т.п.).

Правильность ранжирования вновь определяется условием совпадения расчетных сумм реальных рангов, полученных по таблице и по расчетной формуле (1.3).

Проверим правильность ранжирования для нашего примера.

Реальная сумма рангов такова: 8 + 10 + 12 = 30

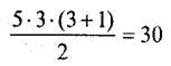
По формуле (1.3) она такова:

Следовательно, ранжирование было проведено правильно.

1.3.3. Случай одинаковых рангов

При выставлении экспертных оценок или в других случаях ранжирования возникают ситуации, когда двум или большему числу качеств приписываются одинаковые ранги. Рассмотрим такой случай применительно к примеру 1.2, в котором ранжировались семь личностных качеств. Для иллюстрации разобьем первый и второй столбцы в таблице 1.2 на две части, представив ее в виде таблицы 1.6:

Таблица 1.6

Я реальное	Качества личности	Яидеальное
		Ответственность
		Общительность		(5)
(3)	2,5	Настойчивость
(2)	2,5	Энергичность		(6)
		Жизнерадостность		(4)
		Терпеливость
		Решительность

Предположим, что при оценке особенностей «Я реального» испытуемый считает, что такие качества как «настойчивость» и «энергичность» должны иметь один и тот же ранг. Тогда при проведении ранжирования (см. столбец № 1 таблицы 1.6) этим качествам необходимо проставить условные ранги, обязательно идущие по порядку друг за другом — и отметить эти ранги круглыми скобками — ( ). Однако, поскольку эти качества, по мнению испытуемого, должны иметь одинаковые ранги, во втором столбце таблицы 1.6, относящемуся к «Я реальному» следует поместить среднее арифметическое рангов, проставленных в скобках, т.е. (2+3)/2=2,5 . Таким образом, второй столбец таблицы 1.6 и будет окончательным итогом ранжирования особенностей «Я реального» данным испытуемым.

Проверим правильность ранжирования. Вначале складываем реальные ранги, полученные во втором столбце таблицы 1.6: 1 + 2, 5 + 2, 5 + 5 + 4 + 6 = 28

Мы помним, что по формуле (1.1) сумма рангов также равнялась 28. Следовательно, ранжирование проведено правильно.

Предположим, что при ранжировании качеств, относящихся к «Я идеальному», испытуемый считает, что таким качествам как: «общительность», «энергичность» и «жизнерадостность» нужно проставить одинаковые ранги. В таком случае этим качествам он ставит условные ранги по порядку в круглых скобках в последнем пятом столбце таблицы 1.6.

Среднее арифметическое условных рангов (4 + 5 + 6)/3 = 5 и есть искомый ранг, который приписывается трем вышеназванным качествам, в четвертом столбце таблицы 1.6

Подчеркнем еще раз, что условные ранги должны располагаться по порядку величин, несмотря на то, что ранжируемые качества не находятся рядом друг с другом.

Проверим опять правильность ранжирования, суммируя полученные в четвертом столбце ранги: 1 + 2 + 3 + 5 + 5 + 5 + 7 = 28

Мы помним, что по формуле (1.1) сумма рангов также равнялась 28. Следовательно, ранжирование проведено правильно.

Одинаковые ранги можно присваивать любому числу ранжируемых величин. В таком случае им также приписывается величина среднего арифметического от количества условных рангов, проставляемых по порядку их величин.

Рассмотрим особенности ранжирования количественных характеристик. Несмотря на то, что ранжирование широко используется применительно к количественным показателям, следует помнить, что в порядковой шкале операции с числами — это по сути дела операции с рангами (порядками), но не с количественным выражением свойств (качеств, признаков и т.п.) как таковых.

В этом случае правила ранжирования таковы:

1. Наименьшему числовому значению приписывается ранг 1.

2. Наибольшему числовому значению приписывается ранг, равный количеству ранжируемых величин.

3. В случае если несколько исходных числовых значений оказались равными, то им приписывается ранг, равный средней величине тех рангов, которые эти величины получили бы, если бы они стояли по порядку друг за другом и не были бы равны.

Отметим, что под этот случай могут попасть как первые, так и последние величины исходного ряда для ранжирования.

4. Общая сумма реальных рангов должна совпадать с расчетной, определяемой по формуле (1.1).

5. Не рекомендуется ранжировать более чем 20 величин (признаков, качеств, свойств и т.п.), поскольку в этом случае ранжирование в целом оказывается малоустойчивым.

6. При необходимости ранжирования достаточно большого числа объектов их следует объединять по какому-либо признаку в достаточно однородные классы (группы), а затем уже ранжировать полученные классы (группы).

Пример 1.2.Психолог получил у 11 испытуемых следующие значения показателя невербального интеллекта: 113, 107, 123, 122, 117, 117, 105, 108, 114, 102, 104. Необходимо проранжировать эти показатели, и лучше всего это сделать в таблице:

Таблица 1.7

№ испытуемых п/п	Показатели интеллекта	Ранги
		(8) 8,5
		(9) 8,5

В этой таблице условные и реальные ранги располагались в одном столбце, что удобнее и экономит много места.

Проверим правильность ранжирования по формуле (1.1): подставляем исходные значения в формулу, получаем: 11∙12/2=66.

Суммируем реальные ранги, получаем:

6 + 4 + 11 + 10 + 8,5 + + 8,5 + 3 + 5 + 7 + 1 + 2 = 66.

Поскольку суммы совпали, следовательно, ранжирование проведено правильно.

В ранговой шкале применяется множество разнообразных статистических методов, часть из которых будет описана ниже. Наиболее часто к измерениям, полученным в этой шкале, применяются коэффициенты корреляции Спирмена и Кэндалла, кроме того, применительно к данным, полученным в этой шкале, используют разнообразные критерии различий.

Шкала интервалов

В шкале интервалов, или интервальной шкале, каждое из возможных значений измеренных величин отстоит от ближайшего на равном расстоянии. Главное понятие этой шкалы — интервал, который можно определить как долю или часть измеряемого свойства между двумя соседними позициями на шкале. Размер интервала — величина фиксированная и постоянная на всех участках шкалы. Для измерения посредством шкалы интервалов устанавливаются специальные единицы измерения; в психологии это стены и стенайны. При работе с этой шкалой измеряемому свойству или предмету присваивается число, равное количеству единиц измерения, эквивалентное количеству имеющегося свойства. Важной особенностью шкалы интервалов является то, что у нее нет естественной точки отсчета (нуль условен и не указывает на отсутствие измеряемого свойства).

Так, в психологии часто используется семантический дифференциал Ч. Осгуда, который является примером измерения по интервальной шкале различных психологических особенностей личности, социальных установок, ценностных ориентации, субъективно-личностного смысла, различных аспектов самооценки и т.п:

Однако, как подчеркивают С. Стивене и ряд других исследователей, психологические измерения в шкале интервалов по сущности нередко оказываются измерениями, выполненными в шкале порядков. Основанием для этого утверждения служит тот факт, что функциональные возможности человека меняются в зависимости от разных условий. При измерении, например, силы с помощью динамометра или устойчивости внимания с помощью секундомера, результаты измерения в начале и в конце опыта по причине усталости испытуемого не будут квантифи-цироваться равными интервалами.

Только измерение по строго стандартизированной тестовой методике, при условии того, что распределение значений в репрезентативной (см. ниже) выборке достаточно близко к нормальному (см. ниже), может считаться измерением в интервальной шкале. Примером последнего могут служить стандартизованные тесты интеллекта, где условная единица измерения IQ эквивален­тна как при низких, так и при высоких значениях интеллекта.

Принципиально важным является и то, что к экспериментальным данным, полученным в этой шкале, применимо достаточно большое число статистических методов.

Шкала отношений

Шкалу отношений называют также шкалой равных отношений. Особенностью этой шкалы является наличие твердо фиксированного нуля, который означает полное отсутствие какого-либо свойства или признака. Шакала отношений является наиболее информативной шкалой, допускающей любые математические операции и использование разнообразных статистических методов.

Шкала отношений по сути очень близка интервальной, поскольку если строго фиксировать начало отсчета, то любая интервальная шкала превращается в шкалу отношений.

Именно в шкале отношений производятся точные и сверхточные измерения в таких науках, как физика, химия, микробиология и др. Измерение по шкале отношений производятся и в близких к психологии науках, таких, как психофизика, психофизиология, психогенетика.

Глава 2

ПОНЯТИЕ ВЫБОРКИ

Психолог-экспериментатор в большинстве случаев изучает какую-то определенную выборку людей, которая всегда отбирается из большей по численности группы. Такая объемлющая группа называется в статистике генеральной совокупностью. Таким образом, генеральная совокупность — это любая группа людей, которую психолог изучает по выборке. Теоретически считается, что объем генеральной совокупности не ограничен. Практически же объем генеральной совокупности всегда ограничен и может быть различным в зависимости от предмета наблюдения и той задачи, которую предстоит решать психологу.

Выборкой называется любая подгруппа элементов (испытуемых, респондентов), выделенная из генеральной совокупности для проведения эксперимента. При этом отдельный индивид из выборки, с которым работает психолог, называется испытуемым (респондентом).

Объем выборки, обычно обозначаемой буквой я, может быть любым, но не меньшим чем два респондента. В статистике различают малую (n ≤ 30), среднюю 30 < n < 100 и большую выборку (n ≥ 100).

2.1. Полное исследование

Если психологическому исследованию (наблюдению, измерению, эксперименту) подвергаются все представители изучаемой генеральной совокупности, то такое исследование называют полным, или сплошным.

Предполагается, что, в соответствии с задачами, гипотезами и планом, полное обследование генеральной совокупности позволяет получить исчерпывающую информацию об изучаемых в ней психологических закономерностях. Однако в отечественной и зарубежной психологии еще никогда не проводилось сплошного исследования по той причине, что на практике определить размеры той или иной генеральной совокупности и тем более исследовать её — задача нереальная и, кроме того, в определенной степени избыточная. Если выборка испытуемых по своим характеристикам репрезентативна генеральной совокупности, то есть основания полученные при её изучении результаты распространить на всю генеральную совокупность. Нельзя упускать из вида также и то, что работа психолога, по существу, представляет собой сложный вид деятельности, требующий высокой профессиональной компетентности и нередко много времени для работы с каждым испытуемым.

2.2. Выборочное исследование

Если психолог производит выбор ограниченного числа элементов из изучаемой (генеральной) совокупности, то такое исследование называют частичным, или выборочным.

Выборочный метод является основным в экспериментальной работе психолога при изучении генеральных совокупностей. Его преимущество перед полным (сплошным) исследованием всех элементов генеральной совокупности заключается в том, что он сокращает как время, так и затраты труда, а главное — позволяет получать информацию о таких группах, полное обследование которых принципиально невозможно или нецелесообразно.