Оцените качество уравнения через среднюю ошибку аппроксимации.

Рассчитаем среднюю ошибку аппроксимации по формуле средней арифметической простой:

Таблица 2 – Данные для расчета средней ошибки аппроксимации

№ п/п	y
	2,50	2,8	0,13
	3,30	2,8	0,15
	2,30	2,7	0,18
	3,30	2,5	0,24
	4,20	3,3	0,23
	2,90	2,8	0,03
	5,70	6,5	0,13
	3,20	3,1	0,03
	8,50	7,8	0,09
	2,00	2,2	0,09
	2,90	2,5	0,15
	3,50	2,8	0,19
	3,50	2,8	0,20
	3,00	3,6	0,20
	2,00	3,0	0,50
	2,40	2,4	0,00
	3,40	3,2	0,05
	2,50	2,8	0,13
	2,70	3,3	0,21
	3,50	2,7	0,22
	0,70	2,9	3,13
	2,90	2,7	0,06
	3,60	2,8	0,23
	2,20	2,3	0,04
	2,30	2,7	0,18
Итого	79,00		6,81

Таким образом, фактические значения результативного признака отличаются от теоретических значений на 27,23 %. Следовательно, построенная модель является удовлетворительной.

Постройте модель в стандартизованном масштабе и проинтерпретируйте ее параметры.

Уравнение в стандартизованном масштабе имеет вид: .

Расчет β – коэффициентов выполним по формулам:

; .

Парные коэффициенты корреляции берутся из матрицы (рисунок 4):

Получим уравнение .

Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результативный признак, если соответствующий фактор изменится на 1 сигму при неизменном среднем уровне других факторов.

В нашем случае, при увеличении использования капитала на 1 сигму чистый доход увеличится на 0,34 сигм, при условии, что численность служащих остаются на прежнем уровне. Аналогично вывод для .

9. Рассчитайте прогнозное значение результата, если прогнозное значение факторов составляют 80% от их максимальных значений.

Рассчитаем ожидаемое прогнозное значение чистого дохода как точечный прогноз путем подстановки в уравнение регрессии прогнозные значения факторов:

1) найдем максимальное значение для фактора 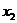(рисунок 7):

2) найдем максимальное значение для фактора 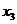(рисунок 7):

3) найдем прогнозные значения факторов:

для фактора :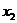

для фактора :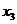

4) подставим прогнозные значения факторов в уравнение . В результате получим:

.

Таким образом, при прогнозных значениях использованного капитала 22 млдр. долл. и численности служащих 229,2 тыс. чел. чистый доход крупнейших компаний США составит 7,47 млрд. долл.

10. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости .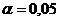

Доверительный интервал прогноза имеет следующий вид:

,

где - средняя ошибка прогнозируемого значения ;

- вектор-столбец прогнозных значений факторов;

- стандартная ошибка .

1) составим вектор-столбец ;

2) найдем транспонируемый вектор-столбец ;

3) из рисунка 4 ;

4) найдем стандартную ошибку ;

5) составим матрицу X - 25 наблюдаемых значений независимых переменных 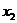и 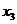, размер которой 25 3 (добавлен единичный столбец для определения a₀);

6) найдем произведение ;

7) найдем ;

8) найдем выражение ;

9) вычислим среднюю ошибку прогнозируемого значения

;

10) по таблицам распределения Стьюдента находим табличное значение при уровне значимости 0,05 и числе степеней свободы 22

;

11) составляем доверительный интервал:

.

Значит, с вероятность 95 % можно сказать, что чистый доход будет колебаться от 6,33 до 8,61 млрд. долл. при использованном капитале в 22 млрд. долл. и численности служащих 229,2 тыс. чел.