Вычисление длинны дуги кривой

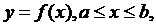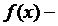Пусть плоская кривая AB задана уравнением где непрерывная функция на отрезке 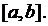Разобьем кривую AB на n произвольных частей точками 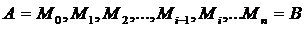в направлении от A к B. Соединив соседние точки хордами, получим некоторую вписанную в кривую AB ломаную, длину которой обозначим через P

(рис. 4.10). Через 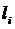обозначим длину одного звена 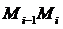ломанной, а через 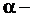длину наибольшего из её звеньев: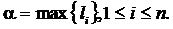

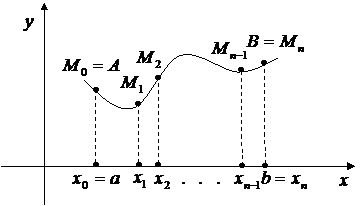Рис. 4.10

Определение: Число L называется пределом длин ломанных P при 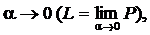если для любого 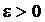существует 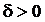такое, что для всякой ломанной, у которой 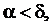выполняется неравенство

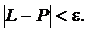
Если существует предел L длин P, вписанных в кривую ломаных при 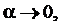то этот предел называется длинной дуги AB. Если функция 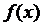непрерывна вместе с 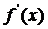на отрезке 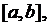то длинна L дуги AB выражается формулой

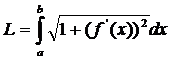(4.12)

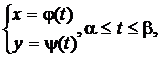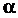При вычислении длины дуги в случае, когда кривая AB задана параметрическими уравнениями где и 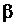- значения параметра t, соответствующие значениям 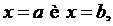т.е. 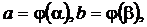формула (4.12) принимает вид:

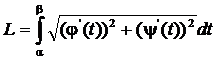
При вычислении длины дуги в случае, когда кривая AB задана в полярных координатах уравнением 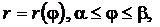где 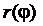имеет непрерывную производную 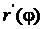на отрезке 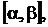и точкам A и B соответствует значения 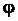, равные 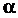и 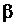, формула (4.12) примет вид

.

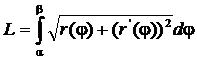Пример.Вычислить длину дуги кривой, заданной в прямоугольной системе координат

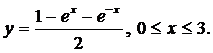
Решение.Найдем производную

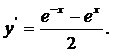
Производная непрерывна, следовательно, можем найти длину дуги кривой по формуле

.

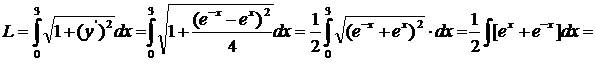
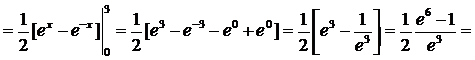
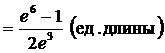Пример. Вычислить длину дуги кривой, заданной параметрическими уравнениями

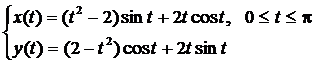
Решение. Функции 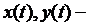непрерывно дифференцируемы.

Найдем 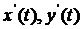и вычислим длину дуги по формуле

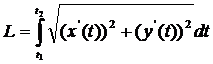
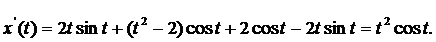
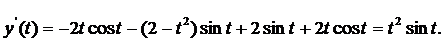
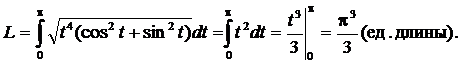
Пример. Вычислить длину дуги кривой, заданной в полярных координатах

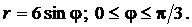
Решение. Кривая 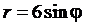представляет собой окружность 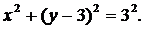Данная кривая непрерывна (рис. 4.11). Длину дуги OAB вычисляем по формуле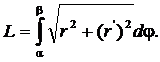

Рис. 4.11

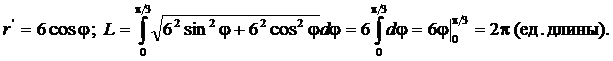
Объем тела вращения.

Если функция 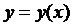знакопостоянна на отрезке 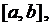то объем 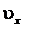тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями 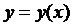, 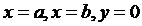(рис. 4.12), вычисляется по формуле

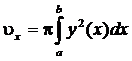
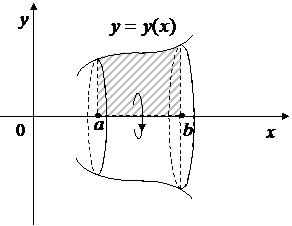Рис. 4.12

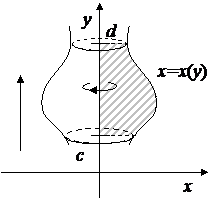Рис. 4.13

Аналогично, объем 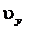тела, образованного при вращении вокруг оси Oy плоской фигуры, ограниченной линиями 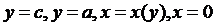(рис. 4.13), вычисляется по формуле

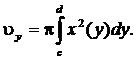
Пример. Эллипс 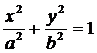вращается вокруг оси Ox, при этом образуется поверхность, называется эллипсоидом вращения. Найти объем тела вращения.

Решение. Построим эллипс в системе координат xOy по данному уравнению.(рис.4.14)

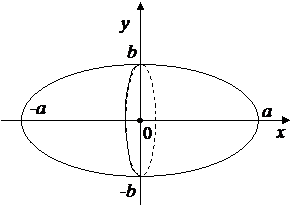Рис. 4.14

Объем тела вращения будем находить по формуле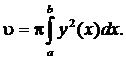

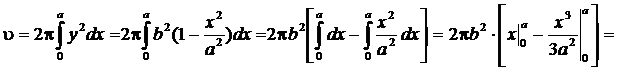
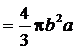(куб. ед.).

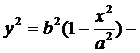найдено из уравнения эллипса.

В частности, при 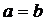вращается окружность, получим объем шара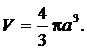

Пример. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций 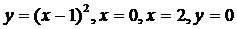вокруг оси Ox.

Решение. Фигура ограниченная кривыми 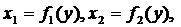где 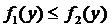и прямыми 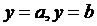вращается вокруг оси Oy. (рис. 4.15)

Объем тела вращения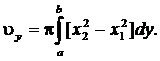

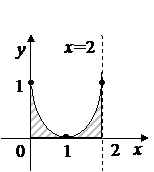
Рис. 4.15

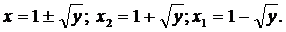
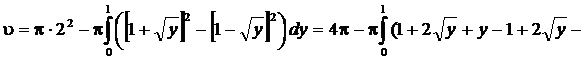
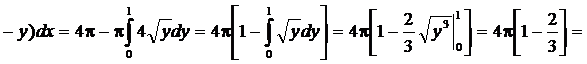
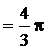(куб. ед.)

Дифференциальные уравнения

Дифференциальные уравнения

Определение 5.1.Дифференциальным уравнением называется уравнение, связывающее независимую переменную x, искомую функцию 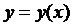и её производные 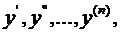т.е. уравнение вида

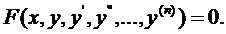
Если искомая функция 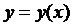есть функция одной независимой переменной x, дифференциальное уравнение называется обыкновенным, например,

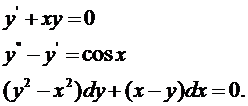
Если искомая функция y есть функция двух и более независимых переменных, то дифференциальное уравнение называется уравнением в частных производных, например,

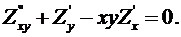
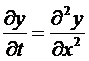
Определение 5.2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

Например, дифференциальное уравнение

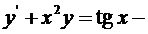уравнение первого порядка.

Определение 5.3. Решением дифференциального уравнения n – го порядка на некотором множестве D называется функция 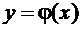, определенная на множестве D вместе со своими производными до n – го порядка включительно и такая, что подстановка функции 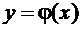в дифференциальное уравнение превращает его в тождество по x на D.