Местные гидравлические сопротивления

Местные гидравлические сопротивления создаются различного рода элементами, установка которых вызывается необходимостью условий эксплуатации трубопроводов. Поток в местных сопротивлениях претерпевает изменение направления или сечения, разделения или соединения, а также различные комбинации указанных случаев, что сопровождается значительными потерями энергии.

Местные потери обычно выражают через скоростной напор, соответствующий средней скорости до сопротивления (v₁) или после сопротивления (v₂)

Δp_м=ϛ₁ ϛ_{2 ,} (4.13)

откуда

= ,

где S₁и S₂— площади живого сечения соответственно до сопротивления и после сопротивления; ϛ₁ и ϛ₂ — коэффициенты местных сопротивлений.Значения коэффициентов местных сопротивлений обычно получают экспериментально, и они приводятся в справочной литературе применительно к скоростному напору за сопротивлением. Значения £ не зависят от числа Рейнольдса при Re> 5000—1000. При меньшихReкоэффициенты ϛ увеличиваются.

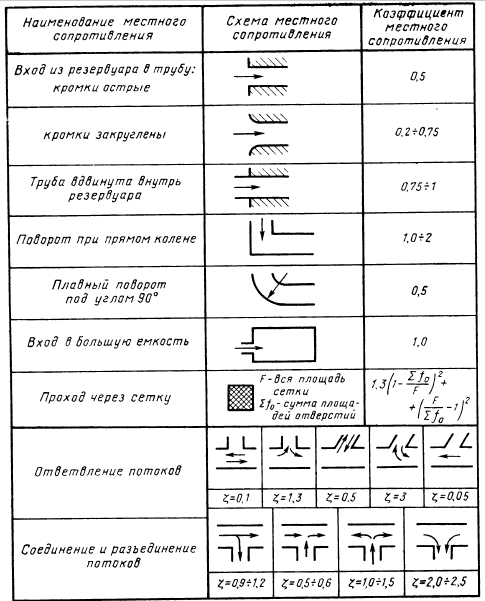
Средние значения коэффициентов наиболее распространенных местных сопротивлений приведены в табл. 2. Кроме того, значениеϛ можно принимать:

для штуцеров, присоединяющих трубы к агрегатам, и переходников, соединяющих отрезки труб ϛ= 0,1 0,15;

для вентилей, ось перехода которых меняет свое направление под прямым углом ϛ= 2 3; если ось прохода не меняет направления ϛ= 0,5 1,0;

для распределительных золотников в зависимости от количества поворотов жидкости ϛ =2 ; для клапанов различного назначения ϛ = 2,5 10; для кранов ϛ = 5,0.

В практике арматура, создающая местные гидравлические сопротивления, может устанавливаться на различных расстояниях друг от друга. При малых расстояниях возможно влияние одного сопротивления на другое и нарушение режима течения потока в прямолинейной части трубопровода.

При последовательном соединении местных сопротивлений поток жидкости стабилизируется, если расстояние между участками с местным сопротивлением не менее

L_M= (20 50) d,

где d— диаметр трубопровода, одинаковый по всей длине трубопровода.

Если это условие соблюдается, то общие потери от местных сопротивлений, включенных последовательно, определяются суммированием отдельных коэффициентов местных сопротивлений, поэтому

Δp_м= (4.14)

где k— число последовательно соединенных местных сопротивлений; ϛ— коэффициент одного местного сопротивления.

Коэффициент местных сопротивления

Таблица 2

В гидравлических расчетах бывает удобно выражать потери давления в местных сопротивлениях через потери в гладкой трубе, поэтому существует понятие эквивалентной длины местного сопротивления, которое определяется из соотношения

Ϛ=λ L=λ (4.15)

т. е. эквивалентная длина выражается через диаметр.

Таким способом трубопровод с местными сопротивлениями в расчете можно заменить эквивалентным трубопроводом, используя зависимость (4.4),

Δp=λ (4.16)

6. Сопротивление при относительном движении

Относительное движение тела и жидкости возможно как при движении тела в покоящейся жидкости, так и при обтекании жидкостью неподвижного тела. В первом случае тело встречает со стороны жидкости сопротивление, для преодоления которого необходима некоторая сила. Во втором случае, наоборот, тело оказывает сопротивление движению жидкости, на преодоление которого затрачивается часть энергии потока обтекающей жидкости.

Полная сила сопротивления, которая возникает при относительном движении тела и жидкости, складывается из равнодействующей элементарных сил трения, направленных по касательной к поверхности обтекаемого тела, и силы давления, являющейся следствием разности давлений на переднюю и заднюю поверхности тела. При движении тела по свободной поверхности жидкости возможно также волновое сопротивление тела

Воздействие потока на твердое тело в общем случае можно свести к вектору, приложенному в некоторой точке, называемой центром давления. Полный вектор, действующий на твердое тело, представляют в виде силы лобового R_л сопротивления, направленной вдоль вектора скорости набегающего потока, и подъемной силы R_п, направленной перпендикулярно. Эти две силы выражают через максимальное миделево сечение тела Sи скоростной напор потока:

R_п=с_пSρ , (4.17)

R_л= с_лSρ , (4.18)

где с_л — коэффициент лобового сопротивления; с_п— коэффициент подъемной силы.

Коэффициенты с_п и с_л определяются экспериментально для тел различной формы; значение этих коэффициентов можно найти в справочной литературе. Для тел выпуклой формы, приближенной к сфере, коэффициент с_л = 0,5 при турбулентном течении, для хорошо окатанного гравия с_п = 1,1, а для кускового угля — 1,2.

В зависимости от соотношения действующих на тело сил возможен подъем этого тела в жидкости, его погружение или состояние равновесия (витания).

Рассмотрим распространенный в практике случай движения тела в восходящем потоке жидкости (рис. 27). Такая задача возникает например, при бурении шпуров и скважин в горных выработках, а также при транспортировании смеси грунта и воды (пульпы). Основной величиной, которую необходимо при этом определить, является критическая скорость восходящего потока, представляющая собой такую скорость течения жидкости, при которой твердая частица остается во взвешенном состоянии.

Пусть частица объемом V и плотностью ρ_т удерживается на весу набегающим со скоростью ν_ж потоком жидкости. Сила тяжести частицы G=ρ_тgVуравновешивается «архимедовой» силой R_A= ρ_жgV, направленной вверх по вертикали, и силой лобового сопротивления, определяемой по формуле (4.18). Из условия равновесия этих сил (равенства проекций этих сил на направление движжия жидкости) получим

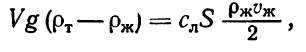
откуда критическая скорость

где S— площадь проекции тела на плоскость, нормальную к направлению движения.

Из формулы (4.19) следует, что при одном и том же значении критической скорости во взвешенном состоянии будут удерживаться тела с большим значением S.

Для тел простейшей геометрической формы (шара, цилиндра и т. п.) формула (4.19) может быть представлена теоретически. Так, для тела, имеющего форму шара, получим

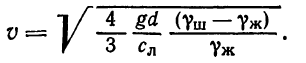(4.20)

При движении пульпы по горизонтальному трубопроводу крупные фракции имеют тенденцию к оседанию на дно трубопровода и тем интенсивнее, чем меньше скорость движения пульпы .Поэтому если средняя скорость движения пульпы окажется меньше некоторой минимальной скорости, то пульповод начнет интенсивно заиляться за счет выпадения на дно взвешенных частиц грунта. Поэтому при расчете пульповодов определяют критическую скорость, которая обеспечивает движение пульпы

без осаждения. Для расчета критической скорости предложены эмпирические зависимости типа (4.19), например

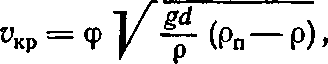
(4.21)

где d—диаметр трубопровода; ρ_п—плотность гидросмеси;φ— опытный коэффициент, зависящий от структуры гидро смеси (при размере твердых частиц 0—25 мм φ= 4,3; при 0—50 ммφ= 4,8).При скорости движения пульпы больше критической гидротранспорт становится неэкономичным из-за большого расхода воды приυ 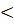υ_кр вследствие оседания на дно крупных фракций; сечение трубы будет уменьшаться и скорость движения пульпы увеличивается до критического значения, что, впрочем, может привести к закупориванию трубопровода