Большие квазиоптимальные композиционные системы ДЧ сигналов

Наилучшими свойствами (максимальным объёмом L и хорошими ВКФ) обладают композиционные системы ДЧ сигналов, полученные путем объединения оптимальных систем, построенных по алгоритму формирования ЧКП согласно четвертой строке табл.3.1 при r≠1 и различных значениях параметра .

При r >1 этот алгоритм является нелинейным, но композиционная система сигналов имеет, при незначительном ухудшении корреляционных свойств, существенно больший объем, по сравнению с рассмотренными выше оптимальными системами. Например, при r=3 объем композиционной системы:

(3.28)

В табл.3.2 (столбец 1) представлен один из таких квазиоптимальных алгоритмов при значениях r=3,5.

Таблица3.2. Алгоритмы построения композиционных систем ДЧ сигналов.

Алгоритм	Изменяемый параметр и пределы изменения.	М	Lmax	Rmax
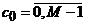r =5 r =3 r =5 r =3 r =5 r =5 r =3	,			3/7 3/11 3/13 3/17 4/17 5/29 3/29

Данный алгоритм построения нелинейных композиционных систем позволяет получать квазиоптимальные системы наибольшего объёма. При этом уровни максимальных пиков R_max ВКФ не превышают значения r/М. Например, большая квазиоптимальная композиционная система при r=3 и М=11 объединяет 11 оптимальных подсистем сигналов с базой М²=121, построенных по алгоритму (табл.3.2) при различных значениях параметра При этом каждая подсистема содержит 10 сигналов, а полный объём такой композиционной системы сигналов.

Оценим объём больших систем ДЧ сигналов. Известно, что полный код ДЧ сигналов имеет объем сигналов

(3.29)

Можно показать при заданном допустимом значении числа совпадений n, что среднее значение объёма искомой большой системы при вероятности p того, что число совпадений т элементов ДЧ сигналов превысит это значение n при М >> n >1 равно:

(3.30)

т.е. растет как факториал (n+1)! и не зависит от М.

При этом относительный объём системы ДЧ сигналов

(3.31)

который при М >> n (т. е. длясистемы ДЧ сигналов с малым числом совпадений) составляет малую долю от полного кода.

Рассмотренные ранее ДСЧ сигналы, например, ДСЧ-ФМ (рис.1.5) являются производными сигналами, так как получаются в результате модуляции одного сложного сигнала другим, т. е. перемножаются два сигнала: исходный и производящий. Например, для сигнала ДСЧ-ФМ (рис.1.5) исходным является ДЧ сигнал первого порядка с М=7, а производящим - дискретный ФМ сигнал из N=5 символов. Производный сигнал состоит из последовательности семи ФМ последовательностей ФМ сигналов из 5 символов каждая, т. е. является последовательностью семи производящих сигналов и получается перемножением исходного и производящего сигналов.

Следует отметить, что кроме рассмотренных выше некоторых матричных алгоритмов формирования ЧД сигналов на основе многоуровневых числовых последовательностей (МЧП) известны [13] другие алгоритмы формирования МЧП согласно классификации, приведенной на рис.3.4.

Рис.3.4. Классификация многоуровневых числовых последовательностей (МЧП).

Согласно классификации все МЧП для систем с ППРЧ можно условно разделить на два класса:

1. МЧП, формируемые с помощью линейных регистров сдвига (ЛРС);

2. МЧП, получаемые в результате вычислений в конечных числовых полях.

Студент может ознакомиться в обзоре [13] с некоторыми из этих алгоритмов формирования и синхронизации МЧП, пригодных для ААСС с ППРЧ и кодовым разделением абонентов. Рассмотрены также алгоритмы формирования МЧП Костаса для радиолокации с ППРЧ, обеспечивающие вид тела неопределенности близкий к идеальному и соответственно минимум погрешностей измерения дальности (1.8) и скорости (1.9).

Кроме того в этом обзоре даны ссылки на литературу по разработке алгоритмов формирования перспективных нелинейных МЧП на основе обобщенных бент - функций и модифицированных бент – последова-тельностей. Такие МЧП по своим авто- и взаимокорреляционным свойствам уступают многим другим последовательностям, но имеют высокую ЭЛС и соответственно структурную скрытность.