М – последовательности. Основные свойства и методы формирования

Среди ФМ сигналов особое место по применению занимают сигналы, кодовые последовательности которых являются ПСП максимальной длины или М – последовательностями.

М – последовательности обладают следующими свойствами:

1. ПСП является периодической с периодом из N импульсов.

2. Величина боковых пиков периодической АКФ ПСП равна .

3. М – последовательность в общем случае состоит из нескольких видов радиоимпульсов (отличающихся начальными фазами, несущими частотами и т.д.). Импульсы различного вида встречаются в периоде примерно одинаковое число раз, т.е. распределены на периоде равновероятно и удовлетворяют условию сбалансированности. Поэтому М – последовательности называют псевдослучайными.

4. Формируются М – последовательности на основе РСЛОС. При этом, если регистр имеет k – разрядов (дискретных элементов задержки) и в М – последовательности используется алфавит из p различных видов импульсов (отличающихся, например, фазами), то

, (2.29)

откуда число разрядов регистра

. (2.30)

Следовательно, значительное увеличение числа импульсов N в периоде М – последовательности вызывает незначительное увеличение числа разрядов регистра, причем нулевая последовательность является запрещенной.

5. АКФ усеченной М – последовательности, понимаемой как непериодическая последовательность с длиной N, имеет величину боковых пиков, близкую к .

Рассмотрим принцип формирования и свойства М –последовательностей. Пусть при р= 2 РСЛОС рис.2.4 состоит из трех ячеек триггеров с функциями дискретных элементов задержки и сумматора.

Рис.2.4. Генератор М–последовательности с периодом N=7.

На триггеры поступают тактовые импульсы сдвига с частотой , каждый из которых вызывает изменение состояния всех триггеров. При этом состояние на выходе каждого триггера становится равным состоянию на его входе для предыдущего такта. Символы состояния принимают два значения, которые условно обозначим 1 и 0.

Правило суммирования символов в двоичной системе счисления – это суммирование по модулю 2 (mod 2).

Пусть в исходном состоянии символ на выходе T₁ равен 1, а на T₂ и T₃ – 0. Т.е. исходное состояние сдвигающего регистра характеризуется комбинацией выходных символов – 100. На входе T₁ символ 0, т.к. символ на выходе сумматора равен . С поступлением очередного тактового сдвигающего импульса символы с входов триггеров переходят на их выходы. Новое состояние регистра описывается комбинацией – 010. На входе T₁ появляется 1 с выхода сумматора. Аналогично определяются и другие состояния регистра. Состояния регистра различны для тактов 1-7, а для последующих тактов они повторяются. Т.к. число разрядов регистра k=3, то число возможных состояний регистра . Нулевая комбинация 000 является запрещенной, т.к. она приводит к обращению в нуль всех символов во всех комбинациях. Поэтому период ПСП (2.29) равен = 7. Если символы непрерывно считывать с входа T₁, то получим периодическую последовательность c периодом N = 7: .

Если считывать последовательности с других триггеров, то получим последовательности, сдвинутые по времени относительно ПСП с входа T₁.

Изменение исходного состояния регистра приводит лишь к сдвигу последовательности во времени.

Число единиц , число нулей , в периоде ПСП удовлетворяет условию сбалансированности. В общем случае при p=2 число единиц в последовательности , а число нулей .

Сумма двух М – последовательностей, сдвинутых относительно друг друга, является М – последовательностью, т.е. удовлетворяет свойству корреляции кода.

Фазоманипулированный действительный сигнал ПСП огибающей (1.15) U(t) рис.1.4 формируется с помощью М – последовательности на основании следующих известных соотношений.

Согласно таблице 2.1 каждому символу 0,1 ЦКП b_n М – последовательности ставится в соответствие радиоимпульс со своей начальной фазой (т.е. видеоимпульс огибающей КП с амплитудой ):

, (2.31)

Поэтому умножению символов a_n (1 и –1) соответствует согласно (2.31) таблица сложения b_n (0 и 1) по модулю 2, т.е.

. (2.32)

Пример. Покажем, как указанные выше соотношения позволяют легко вычислить, например, АКФ (2.19) для периодического ШПС

.

Если сдвиг не кратен периоду ( для любого l=0,1,…), то согласно (2.32) сумма двух сдвинутых М – последовательностей является М – последовательностью, для которой число единиц больше числа нулей на единицу. Поэтому сумма всех ЦКП при будет равна единице и в выражении для АКФ сумма произведений КП согласно (2.32) и (2.31) равна соответственно минус 1, а нормированная АКФ будет равна (- .)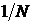

Если сдвиг кратен периоду ( для любого l=0,1,…) временной сдвиг между последовательностями равен нулю, т.е. и значение периодической АКФ равно .

На рис.2.5. представлена периодическая М – последовательность и ее периодическая АКФ, которая при увеличении N приближается к идеальной с уровнем боковых пиков = (−1/N) → 0.

U(t)

1

t

-1 Т 2Т

0 0

Рис.2.5. АКФ периодической М – последовательности с N=15.

Вместе с тем, с точки зрения параметрической скрытности структуры генератора ПСП необходимо также увеличивать период N ПСП. Однако, это требование неэффективно. Известно [2,5,6], что постановщику помех достаточно принять 2k символов М – последовательности, чтобы определить структуру генератора. Поэтому применяют нелинейные ПСП, смену ПСП.

В некоторых приложениях, например, в системах СDМА каждому абоненту присваивается индивидуальная ПСП и ансамбль ПСП должен быть большим. В идеальном случае ПСП абонентов должны быть взаимно ортогональны, т.е. периодическая ВКФ (2.18) равна R_jk (µ) = 0. Однако, число М – последовательностей ограничено, а ВКФ между парами ансамбля реальных М – последовательностей имеет относительно большие амплитуды пиков R_{jk max} (µ). Только отдельные пары ПСП [2] длиной имеют меньшие пики ВКФ с тремя уровнями {-1, -t(k), t(k) -2}, где

(2.32')

Такие М – последовательности называют ПСП Голда, Касами или предпочтительными последовательностями. Например, при k=5 общее число ПСП ансамбля равно 6, R_{jk max} (µ) =11, R_{jk max} (µ)/ R(0) = 0,35 , а для пары предпочтительных ПСП ансамбля t(k=5)=2³+1=9, R_{jk max} (µ)/ R(0) = 0,29.

Рассмотрим обобщенную структуру цифрового автомата рис.2.6 формирования М – последовательностей.

Пусть используется алфавит из p различных символов: 0,1,2,3,…,p-1, образующих множество символов . Cимволы на выходе триггеров в j –м такте равны: x_1,j, x_2,j… x_l,j… x_k,j , а множители . Операция умножения в умножителе X производится по модулю , т.е. . Для сохранения однозначности значения p -простые числа.

Tk

T3

T2

T1

x_0,j x_1,j x_2,j x_3,j x_k,j

C₀

C₁ C₂ C₃ C_k-1 C_k

Рис.2.6. Цифровой автомат формирования М-последовательности.

Правило умножения двух чисел по модулю p: два числа перемножаются обычным образом, а их произведение переводится в конечное множество S с помощью сравнения по модулю p.

Примечание [18]. Два целых числа m и n сравнимы по модулю М, т.е. , где М - целое число, если разность (m - n) делится на М без остатка. Это значит, что m и n при делении на М дают одинаковые остатки. Например, числа: b ≡12 ≡ 2 ≡ −3 (mod 5) сравнимы по mod 5, так как при m=2, n= −3 → (m − n)= 2 − (−3) ≡ 0(mod 5), а 12 ≡ 2(mod 5).

Если все числа m и n при делении на mod M дают одинаковые остатки, т.е. сравнимы, то их можно объединить в один класс, который называют классом вычетов по mod M, а эти числа называют вычетами этого класса. Таким образом, все числа можно разбить на М непересекающихся классов вычетов: С₀ , С₁ ,….С_{М -1} .

Таким образом, умножение по модулю pзаписывается как , при ; например, если a=2, b=4, то d=8,и для p=5 имеет , т.е. число 8, которого нет в множестве S, переводится в число 3. В табл. 2.3 дано правило умножения по mod 5, а в табл. 2.4 правило сложения mod 5.

Таблица 2.3. Умножение по mod 5

Умножение любого числа на нуль означает, что символ на выходе умножителя всегда нуль. Это эквивалентно разрыву цепи между триггером и сумматором и умножитель может быть опущен.

Таблица 2.4. Сложение по mod 5.

В результате операций умножения и сложения получаются только элементы множества S.

Символ на входе T₁ сдвигающего регистра (рис.2.6) на j – такте равен: . (2.33)

Это линейное рекуррентное уравнение позволяет по известным k символам на выходах триггеров найти символ , который в последующем j+1 такте перейдет на выход T₁. Для j+1 – такта состояние РС характеризуется переменными:

. (2.34)

Анализ работы цифрового автомата формирования ПСП на основе рекуррентного уравнения (2.33) показывает, что его работа полностью характеризуется характеристическим многочленом:

, (2.35)

где k – максимальное число ячеек задержки РС (степень свободы состояния генератора), а коэффициенты связаны с множителями соотношением:

. (2.36)

В частности, для двоичных последовательностей, состоящих из символов 1 и 0 (p=2) , .

Характеристический многочлен f(x) степени k формирователя М – последовательности должен быть:

1) неприводимым, то есть его нельзя представить в виде произведения многочленов меньших степеней;

2) первообразным (примитивным) относительно двучлена , то есть должен делить без остатка.

Таким образом, при заданных N, k и p структура регистра для формирования М–последовательности с периодом определяется характеристическим многочленом, в качестве которого необходимо взять первообразный многочлен степени k .

Значения (k+1) коэффициентов..а_kа_k--1 …а₁ а₀ характеристических многочленов для k=3 -11 приведены в таблице [1, таблица 3.9], например:

● для k =3 существует два характеристических многочлена: 1011 и 1101.Коэффициент a₀=1 всегда по определению. Если коэффициент или соответствующий множитель С_l в (2.36) равен 1, то выход l-го триггера подключен к сумматору по mod 2, например, генератор ПСП рис.2.4 соответствует многочлену с коэффициентами 1011;

● для k =5 существует шесть многочленов, два из которых (101001 и 111011) формируютпредпочтительные ПСП Голда с периодом и тремя уровнями ВКФ (2.32').

Число М – последовательностей Q ансамбля ПСП равно

, (2.37)

где - функция Эйлера [1, 17], равная количеству чисел в ряду 1,2,…,N-1 взаимно простых с числом N, где , а k – число разрядов в РС.

Если N–простое число, то . Однако, не все периоды N

М – последовательностей являются простыми числами и поэтому зависимость Q от k нелинейная.

Длительность (период) М–последовательности , например, для РС при f _Т =1/τ₀ =1МГц и k = 43 равна 101,7 дня.